新课标A版必修1 》第二章基本初等函数(Ⅰ) 》幂函数
文档属性
| 名称 | 新课标A版必修1 》第二章基本初等函数(Ⅰ) 》幂函数 |

|
|
| 格式 | rar | ||
| 文件大小 | 739.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-04 00:00:00 | ||
图片预览





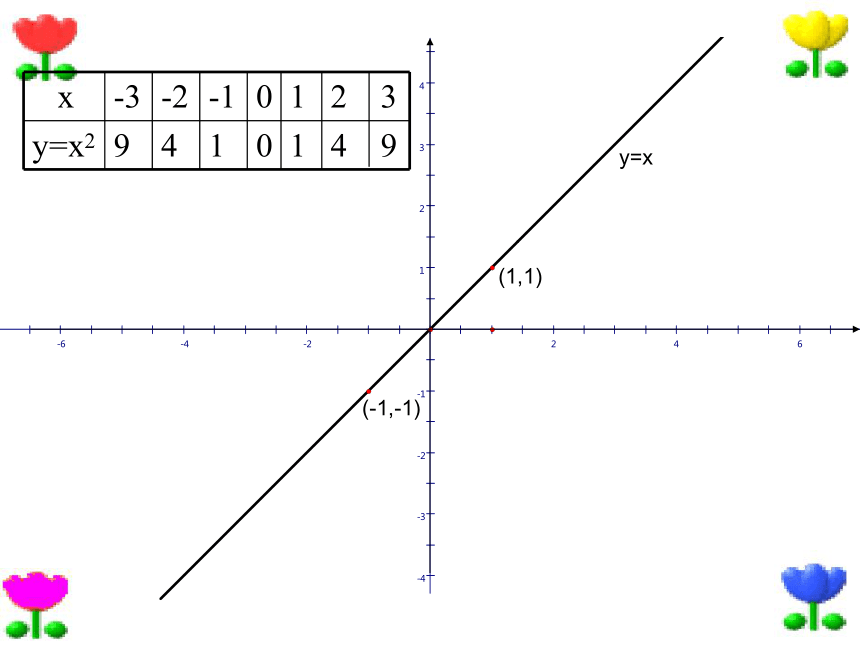
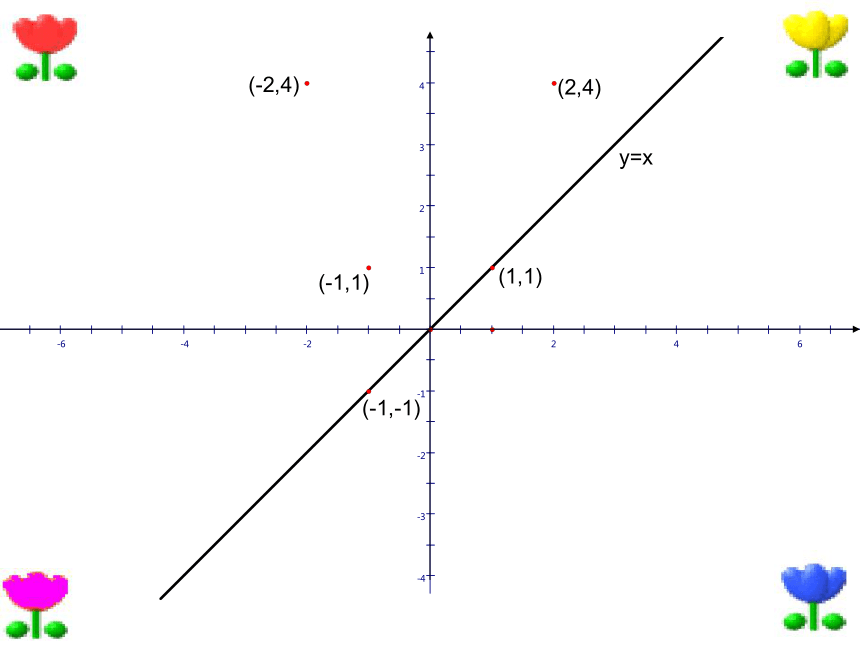
文档简介
课件26张PPT。2.3幂
函
数制作 zengjiti (1)如果张红购买了每千克1元的蔬菜w千克,那么她需要支付P = ______
w 元(2)如果正方形的边长为 a,那么正方形的面积S = ____(3)如果立方体的边长为a,那么立方体的体积V = ____
(5)如果某人 t s内骑车行进1 km,那么他骑车的平均速度v=__________
____是____的函数a2 a3 V是a的函数t?1 km/s v是t 的函数我们先来看几个具体的问题:(4)如果一个正方形场地的面积为 S,那么正方形的边长_________a是S的函数以上问题中的函数具有什么共同特征?思考:Pwy=xy=x2y=x3y=xy=x-1____是____的函数Sa一般地,函数 叫做幂函数(power fun_ction) ,
其中x为自变量, 为常数。[定义:]问题:你能说出幂函数与指数函数的区别吗?注意:幂函数的解析式必须是y = xK 的形式, 其特征可归纳为“两个系数为1,只有1项”.指数函数:解析式 ,底数为常数a,a>0,a≠1,指数为自变量x;幂函数:解析式 ,底数为自变量x,指数为常数α, α∈R;练习1、下列函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=2x (4)y=1
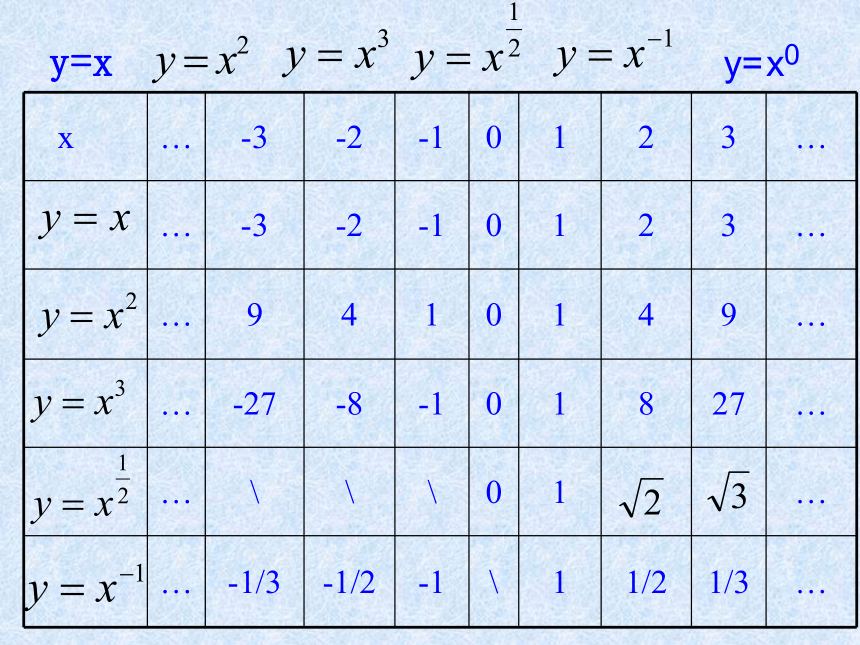
(5) y=x2 +2 (6) y=-x3答案:(1)(4)下面研究幂函数在同一平面直角坐标系内作出这
六个幂函数的图象.
结合图象,研究性质:定义域、值域、单调性、奇偶性、过定点的情况等。研究 y=xy=x在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当k>0时,图象随x增大而上升。
当k<0时,图象随x增大而下降
不管指数是多少,图象都经过哪个定点?在第一象限内,
当k>0时,图象随x增大而上升。
当k<0时,图象随x增大而下降。图象都经过点(1,1)K>0时,图象还都过点(0,0)点奇偶
奇非奇
非偶奇(1,1)RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,观察幂函数图象,将你发现的结论写在下表:在R上增在[0,+∞)上增,在(-∞,0]上减,在[0,+∞)上增,在(0,+∞)上减例1
如果函数 是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数m的集合。解:依题意,得解方程,得 m=2或m=-1检验:当 m=2时,函数为符合题意.当m=-1时,函数为不合题意,舍去.所以m=2
解:(1)y= x0.8在(0,+∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x0.3在(0,+∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3(3)y=x-2/5在(0,+∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5 练习2<<>≤练习3: 如图所示,曲线是幂函数 y = xk 在第一象限内的图象,已知 k分别取 四个值,则相应图象依次为:________ 一般地,幂函数的图象在直线x=1
的右侧,大指数在上,小指数在下,
在Y轴与直线x =1之间正好相反。 C4C2C3C11证明幂函数 在[0,+∞)上是增函数.复习用定义证明函数的单调性的步骤:(1). 设x1, x2是某个区间上任意二值,且x1<x2;(2). 作差 f(x1)-f(x2),变形 ;(3). 判断 f(x1)-f(x2) 的符号;(4). 下结论.例3证明:任取所以幂函数 在[0,+∞)上是增函数. 证法二: 任取x1 ,x2 ∈[0,+∞),且x1< x2 ; 证明幂函数 在[0,+∞)上是增函数.(1)作差法:若给出的函数是有根号的式子,往往采用有理化的方式。
(2)作商法:证明时要注意分子和分母均为正数,否则不一定能推出f(x1)<f(x2)。即所以幂函数定义五个特殊幂函数图象基本性质本节知识结构:作业:P79习题2.3: 1,2,3.谢谢光临,再见
函
数制作 zengjiti (1)如果张红购买了每千克1元的蔬菜w千克,那么她需要支付P = ______
w 元(2)如果正方形的边长为 a,那么正方形的面积S = ____(3)如果立方体的边长为a,那么立方体的体积V = ____
(5)如果某人 t s内骑车行进1 km,那么他骑车的平均速度v=__________
____是____的函数a2 a3 V是a的函数t?1 km/s v是t 的函数我们先来看几个具体的问题:(4)如果一个正方形场地的面积为 S,那么正方形的边长_________a是S的函数以上问题中的函数具有什么共同特征?思考:Pwy=xy=x2y=x3y=xy=x-1____是____的函数Sa一般地,函数 叫做幂函数(power fun_ction) ,
其中x为自变量, 为常数。[定义:]问题:你能说出幂函数与指数函数的区别吗?注意:幂函数的解析式必须是y = xK 的形式, 其特征可归纳为“两个系数为1,只有1项”.指数函数:解析式 ,底数为常数a,a>0,a≠1,指数为自变量x;幂函数:解析式 ,底数为自变量x,指数为常数α, α∈R;练习1、下列函数中,哪几个函数是幂函数?
(1)y = (2)y=2x2
(3)y=2x (4)y=1
(5) y=x2 +2 (6) y=-x3答案:(1)(4)下面研究幂函数在同一平面直角坐标系内作出这
六个幂函数的图象.
结合图象,研究性质:定义域、值域、单调性、奇偶性、过定点的情况等。研究 y=xy=x在第一象限内,函数图象的变化趋势与指数有什么关系?在第一象限内,
当k>0时,图象随x增大而上升。
当k<0时,图象随x增大而下降
不管指数是多少,图象都经过哪个定点?在第一象限内,
当k>0时,图象随x增大而上升。
当k<0时,图象随x增大而下降。图象都经过点(1,1)K>0时,图象还都过点(0,0)点奇偶
奇非奇
非偶奇(1,1)RRR{x|x≠0}[0,+∞)RR{y|y≠0}[0,+∞)[0,+∞)在R上增在(-∞,0)上减,观察幂函数图象,将你发现的结论写在下表:在R上增在[0,+∞)上增,在(-∞,0]上减,在[0,+∞)上增,在(0,+∞)上减例1
如果函数 是幂函数,且在区间(0,+∞)内是减函数,求满足条件的实数m的集合。解:依题意,得解方程,得 m=2或m=-1检验:当 m=2时,函数为符合题意.当m=-1时,函数为不合题意,舍去.所以m=2
解:(1)y= x0.8在(0,+∞)内是增函数,
∵5.2<5.3 ∴ 5.20.8 < 5.30.8 (2)y=x0.3在(0,+∞)内是增函数
∵0.2<0.3∴ 0.20.3 <0.30.3(3)y=x-2/5在(0,+∞)内是减函数
∵2.5<2.7∴ 2.5-2/5>2.7-2/5 练习2<<>≤练习3: 如图所示,曲线是幂函数 y = xk 在第一象限内的图象,已知 k分别取 四个值,则相应图象依次为:________ 一般地,幂函数的图象在直线x=1
的右侧,大指数在上,小指数在下,
在Y轴与直线x =1之间正好相反。 C4C2C3C11证明幂函数 在[0,+∞)上是增函数.复习用定义证明函数的单调性的步骤:(1). 设x1, x2是某个区间上任意二值,且x1<x2;(2). 作差 f(x1)-f(x2),变形 ;(3). 判断 f(x1)-f(x2) 的符号;(4). 下结论.例3证明:任取所以幂函数 在[0,+∞)上是增函数. 证法二: 任取x1 ,x2 ∈[0,+∞),且x1< x2 ; 证明幂函数 在[0,+∞)上是增函数.(1)作差法:若给出的函数是有根号的式子,往往采用有理化的方式。
(2)作商法:证明时要注意分子和分母均为正数,否则不一定能推出f(x1)<f(x2)。即所以幂函数定义五个特殊幂函数图象基本性质本节知识结构:作业:P79习题2.3: 1,2,3.谢谢光临,再见
