22.1.1 二次函数 课件(共20张PPT) 2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 22.1.1 二次函数 课件(共20张PPT) 2023-2024学年人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 356.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
第二十二章 二次函数
22.1 二次函数的图像和性质
22.1.1 二次函数
1.知道二次函数的概念,会判断一个函数是否是二次函数;(重点)
2.会表示一个变化过程中的二次函数关系.(难点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
回顾:
什么叫函数?我们已经学过哪些函数?
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,
另一个变量y总有唯一的值与它对应.
这样的两个变量之间的关系我们把它叫做函数关系.
对于上述变量x 、y,我们把y叫x的函数. x叫自变量, y叫因变量.
我们已经学过一次函数:y=kx+b(k≠0).
那什么是二次函数呢?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
我们先通过几个问题来了解二次函数.
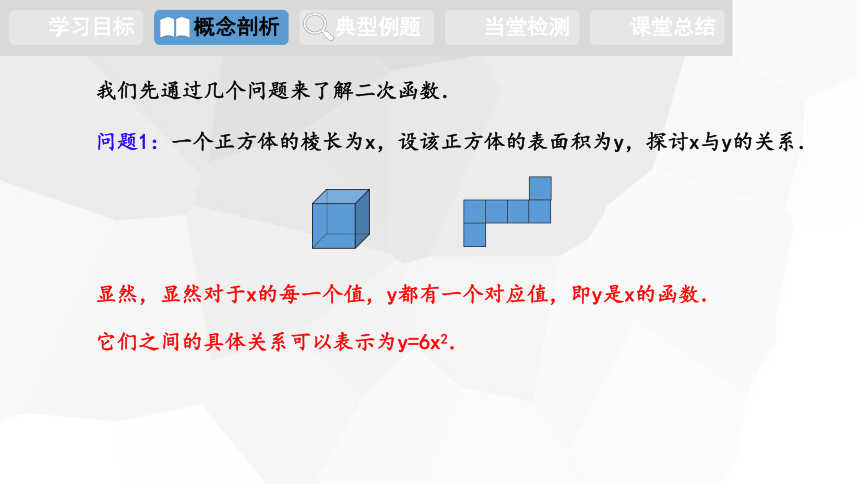
问题1:一个正方体的棱长为x,设该正方体的表面积为y,探讨x与y的关系.
显然,显然对于x的每一个值,y都有一个对应值,即y是x的函数.
它们之间的具体关系可以表示为y=6x2.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题2:某次会议有n个人参加,会议开始前每两人需要握一次手.总握手次
数m与人数n之间有什么关系?
每个人要和其他(n-1)个人各握手一次,A和B的握手,与B和A的握手是同一
次握手,所以总握手次数是
m= n(n-1).
即
m= n2- n.
上式表示总握手次数m与人数n之间的关系,对于n的每一个值,m都
有一个对应值,即m是n的函数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题3:为了响应公益环保活动,某单位组织员工植树;今年一共植树200棵,计划今后两年增加棵数.如果每年都比上一年的棵数增加x倍,那么后年该公司植棵数为y,y与x之间的关系应怎样表示?
明年植树棵数为200(1+x),后年植树棵数为200(1+x)2.
∴y=200(1+x)2,
对于x的每一个值,y都有一个对应值,即y是x的函数.
即y=200x2+400x+200.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
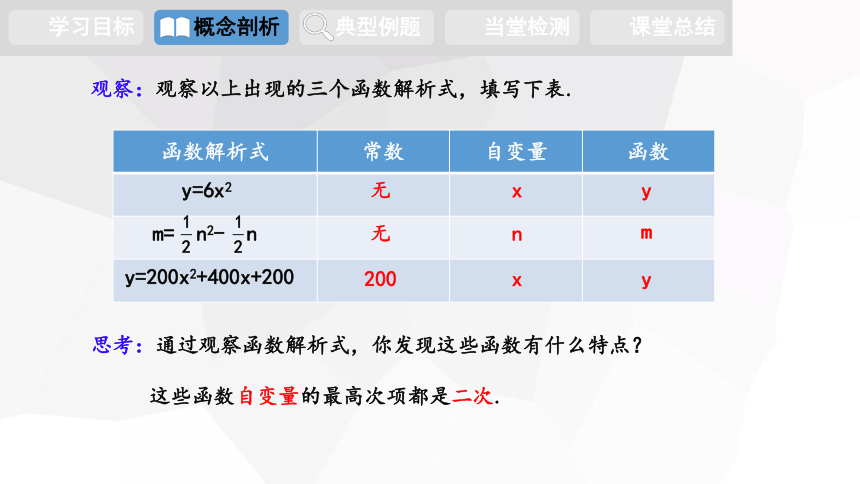
观察:观察以上出现的三个函数解析式,填写下表.
函数解析式 常数 自变量 函数
m= n2- n
y=6x2
y=200x2+400x+200
无
无
y
200
n
x
m
y
x
思考:通过观察函数解析式,你发现这些函数有什么特点?
这些函数自变量的最高次项都是二次.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
总结:
一般形式: y=ax2+bx+c(a,b,c是常数,a≠0).
如果函数解析式是关于自变量的二次多项式,这样的函数叫二次函数.
二次函数的定义
其中,x是自变量, ax2是二次项,a是二次向系数;
bx是一次项,b是一次项系数;
c是常数项.
1. 自变量的最高次数是2.
3. 二次项的系数a不能为0.
2. 二次函数解析式必须是整式.
注意:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
讨论:二次函数y=ax2+bx+c,二次项的系数a为什么不能为0?
当a=0时,函数解析式y=ax2+bx+c变为y=bx+c;这时它就是一次函数.
一次项系数b、常数项c可以为0吗?
当b=0时,函数解析式y=ax2+bx+c变为y=ax2+c;
当C=0时,函数解析式y=ax2+bx+c变为y=ax2+bx;
这时函数仍然满足二次函数的定义;所以b、c可以为0.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.判断下列的函数是否为二次函数.
(1)y=x2
(4)y=x3+x2+x
(3)y=22+x
(5)s=2-t2
(6)s=πr2
(2)y=x2+1
(7)y=
(8)y=(x+1)2-x2
是
是
是
是
否
否
否
否
(3)中自变量最高次项为1,(4)中自变量最高次项为3,
(7)中解析式不是整式,(8)中化简后自变量最高次项为1.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
y=ax +bx+c有几种不同的表示形式:
(1)y=ax (a≠0,b=0,c=0,).
(2)y=ax +c(a≠0,b=0,c≠0).
(3)y=ax +bx(a≠0,b≠0,c=0).
总结:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.下列函数中,哪些是二次函数.
(1)y=x2
(2)y=
(3)y=x(3+x)
(4)y=2(x-1)2 -2x2
是
否
否
是
注意:对于无法直接进行判断的函数,要先进行化简.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.在二次函数y=(x+1)2中,自变量是 ,一次项系数是 ,二次项
系数是 ,常数项是 .
x
1
2
1
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.根据下面的条件列出函数解析式,并判断列出的函数是否为二次函数.
(1)两个数中,一个比另一个大5,这两个数的乘积p是较大的数m的函数;
解:(2)剩余的面积S(cm2)与方孔边长x(cm)的函数关系为:
S=100π-4x2,是二次函数;
解:(1)这两个数的乘积p与较大的数m的函数关系为:
p=m(m-5)=m2-5m,是二次函数;
(2)一个半径为10cm的圆上,挖掉4个大小相同的正方形孔,剩余的面积S
(cm2)是方孔边长x(cm)的函数;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(3)有一块长为60m、宽为40m的矩形绿地,计划在它的四周相同的宽度内种
植阔叶草,中间种郁金香,那么郁金香的种植面积S(m2)是草坪宽度a(m)的函数.
解:(3)郁金香的种植面积S(cm2)与草坪宽度a(m)的函数关系为:
S=(60-2a)(40-2a)=4a2-200a+2400,是二次函数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆面积S与半径R之间的关系
D
解:A:y=kx+b,B:t=s/v,C:C=3a,D:S=πR2.
只有D选项是二次函数,故选D.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例3.若y=(m-1)x 是关于x的二次函数,则m的值为
则m2+m=2且m-1≠0.
解得:m=-2.
故m的值为-2.
m2+m
分析:由题意得,m需满足m2+m=2且m-1≠0.
解:若y=(m+1)x 是关于x的二次函数,
m2+m
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如果y=(k-3)x2+k(x-3)是二次函数,那么k需满足的条件是 .
k≠3
分析:由二次函数的定义得二次项系数不能为0,故k-3≠0.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.已知函数y=(m2-m)x2+mx-2(m为常数),根据下列条件求m的值:
(1)y是x的一次函数;
(2)y是x的二次函数.
解:(1)y是x的一次函数,则可以知道,m2-m=0,
解得:m=1或m=0,又因为m≠0,所以,m=1.
(2)y是x的二次函数,只须m2-m≠0,
∴m≠1和m≠0.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠0)的函数叫做
二次函数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.y=ax +bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax (a≠0,b=0,c=0,).
(2)y=ax +c(a≠0,b=0,c≠0).
(3)y=ax +bx(a≠0,b≠0,c=0).
第二十二章 二次函数
22.1 二次函数的图像和性质
22.1.1 二次函数
1.知道二次函数的概念,会判断一个函数是否是二次函数;(重点)
2.会表示一个变化过程中的二次函数关系.(难点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
回顾:
什么叫函数?我们已经学过哪些函数?
在某变化过程中的两个变量x、y,当变量x在某个范围内取一个确定的值,
另一个变量y总有唯一的值与它对应.
这样的两个变量之间的关系我们把它叫做函数关系.
对于上述变量x 、y,我们把y叫x的函数. x叫自变量, y叫因变量.
我们已经学过一次函数:y=kx+b(k≠0).
那什么是二次函数呢?
典型例题
当堂检测
学习目标
课堂总结
概念剖析
我们先通过几个问题来了解二次函数.
问题1:一个正方体的棱长为x,设该正方体的表面积为y,探讨x与y的关系.
显然,显然对于x的每一个值,y都有一个对应值,即y是x的函数.
它们之间的具体关系可以表示为y=6x2.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题2:某次会议有n个人参加,会议开始前每两人需要握一次手.总握手次
数m与人数n之间有什么关系?
每个人要和其他(n-1)个人各握手一次,A和B的握手,与B和A的握手是同一
次握手,所以总握手次数是
m= n(n-1).
即
m= n2- n.
上式表示总握手次数m与人数n之间的关系,对于n的每一个值,m都
有一个对应值,即m是n的函数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题3:为了响应公益环保活动,某单位组织员工植树;今年一共植树200棵,计划今后两年增加棵数.如果每年都比上一年的棵数增加x倍,那么后年该公司植棵数为y,y与x之间的关系应怎样表示?
明年植树棵数为200(1+x),后年植树棵数为200(1+x)2.
∴y=200(1+x)2,
对于x的每一个值,y都有一个对应值,即y是x的函数.
即y=200x2+400x+200.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
观察:观察以上出现的三个函数解析式,填写下表.
函数解析式 常数 自变量 函数
m= n2- n
y=6x2
y=200x2+400x+200
无
无
y
200
n
x
m
y
x
思考:通过观察函数解析式,你发现这些函数有什么特点?
这些函数自变量的最高次项都是二次.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
总结:
一般形式: y=ax2+bx+c(a,b,c是常数,a≠0).
如果函数解析式是关于自变量的二次多项式,这样的函数叫二次函数.
二次函数的定义
其中,x是自变量, ax2是二次项,a是二次向系数;
bx是一次项,b是一次项系数;
c是常数项.
1. 自变量的最高次数是2.
3. 二次项的系数a不能为0.
2. 二次函数解析式必须是整式.
注意:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
讨论:二次函数y=ax2+bx+c,二次项的系数a为什么不能为0?
当a=0时,函数解析式y=ax2+bx+c变为y=bx+c;这时它就是一次函数.
一次项系数b、常数项c可以为0吗?
当b=0时,函数解析式y=ax2+bx+c变为y=ax2+c;
当C=0时,函数解析式y=ax2+bx+c变为y=ax2+bx;
这时函数仍然满足二次函数的定义;所以b、c可以为0.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例1.判断下列的函数是否为二次函数.
(1)y=x2
(4)y=x3+x2+x
(3)y=22+x
(5)s=2-t2
(6)s=πr2
(2)y=x2+1
(7)y=
(8)y=(x+1)2-x2
是
是
是
是
否
否
否
否
(3)中自变量最高次项为1,(4)中自变量最高次项为3,
(7)中解析式不是整式,(8)中化简后自变量最高次项为1.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
y=ax +bx+c有几种不同的表示形式:
(1)y=ax (a≠0,b=0,c=0,).
(2)y=ax +c(a≠0,b=0,c≠0).
(3)y=ax +bx(a≠0,b≠0,c=0).
总结:
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.下列函数中,哪些是二次函数.
(1)y=x2
(2)y=
(3)y=x(3+x)
(4)y=2(x-1)2 -2x2
是
否
否
是
注意:对于无法直接进行判断的函数,要先进行化简.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.在二次函数y=(x+1)2中,自变量是 ,一次项系数是 ,二次项
系数是 ,常数项是 .
x
1
2
1
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例2.根据下面的条件列出函数解析式,并判断列出的函数是否为二次函数.
(1)两个数中,一个比另一个大5,这两个数的乘积p是较大的数m的函数;
解:(2)剩余的面积S(cm2)与方孔边长x(cm)的函数关系为:
S=100π-4x2,是二次函数;
解:(1)这两个数的乘积p与较大的数m的函数关系为:
p=m(m-5)=m2-5m,是二次函数;
(2)一个半径为10cm的圆上,挖掉4个大小相同的正方形孔,剩余的面积S
(cm2)是方孔边长x(cm)的函数;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
(3)有一块长为60m、宽为40m的矩形绿地,计划在它的四周相同的宽度内种
植阔叶草,中间种郁金香,那么郁金香的种植面积S(m2)是草坪宽度a(m)的函数.
解:(3)郁金香的种植面积S(cm2)与草坪宽度a(m)的函数关系为:
S=(60-2a)(40-2a)=4a2-200a+2400,是二次函数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
3.下列函数关系中,是二次函数的是( )
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系
B.当距离一定时,火车行驶的时间t与速度v之间的关系
C.等边三角形的周长C与边长a之间的关系
D.圆面积S与半径R之间的关系
D
解:A:y=kx+b,B:t=s/v,C:C=3a,D:S=πR2.
只有D选项是二次函数,故选D.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例3.若y=(m-1)x 是关于x的二次函数,则m的值为
则m2+m=2且m-1≠0.
解得:m=-2.
故m的值为-2.
m2+m
分析:由题意得,m需满足m2+m=2且m-1≠0.
解:若y=(m+1)x 是关于x的二次函数,
m2+m
典型例题
当堂检测
学习目标
课堂总结
概念剖析
4.如果y=(k-3)x2+k(x-3)是二次函数,那么k需满足的条件是 .
k≠3
分析:由二次函数的定义得二次项系数不能为0,故k-3≠0.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5.已知函数y=(m2-m)x2+mx-2(m为常数),根据下列条件求m的值:
(1)y是x的一次函数;
(2)y是x的二次函数.
解:(1)y是x的一次函数,则可以知道,m2-m=0,
解得:m=1或m=0,又因为m≠0,所以,m=1.
(2)y是x的二次函数,只须m2-m≠0,
∴m≠1和m≠0.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.定义:一般地,形如y=ax +bx+c(a,b,c是常数,a≠0)的函数叫做
二次函数.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.y=ax +bx+c(a,b,c是常数,a≠0)的几种不同表示形式:
(1)y=ax (a≠0,b=0,c=0,).
(2)y=ax +c(a≠0,b=0,c≠0).
(3)y=ax +bx(a≠0,b≠0,c=0).
同课章节目录
