24.1.4 第2课时 圆内接四边形 课件(共15张PPT) 2023-—2024学年人教版数学九年级上册
文档属性
| 名称 | 24.1.4 第2课时 圆内接四边形 课件(共15张PPT) 2023-—2024学年人教版数学九年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 463.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 11:21:59 | ||
图片预览



文档简介
(共15张PPT)
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角 第2课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.知道圆内接多边形和多边形的外接圆的定义;
2.能说出圆内接四边形的性质,并能灵活运用该性质解决问题.
复习导入:
问题 1:什么是圆周角?
概念:顶点在圆上,并且两边都和圆相交的角叫圆周角;
特征:① 角的顶点在圆上;
② 角的两边都与圆相交.
O
A
E
C
D
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
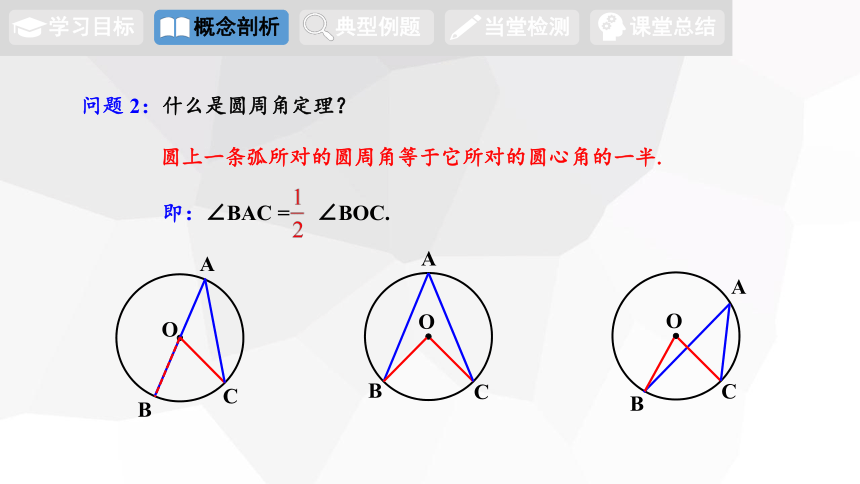
问题 2:什么是圆周角定理?
圆上一条弧所对的圆周角等于它所对的圆心角的一半.
即:∠BAC = ∠BOC.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
B
A
C
O
B
A
C
O
B
A
C
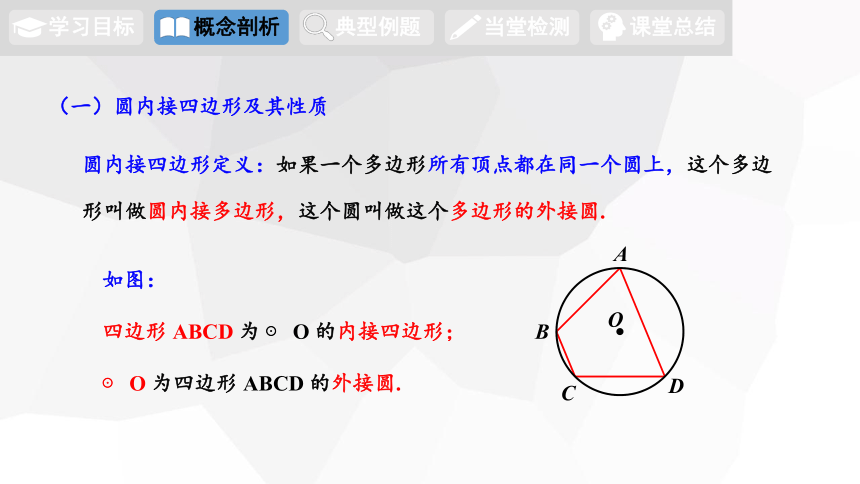
(一)圆内接四边形及其性质
圆内接四边形定义:如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如图:
四边形 ABCD 为 ⊙ O 的内接四边形;
⊙ O 为四边形 ABCD 的外接圆.
O
B
A
C
D
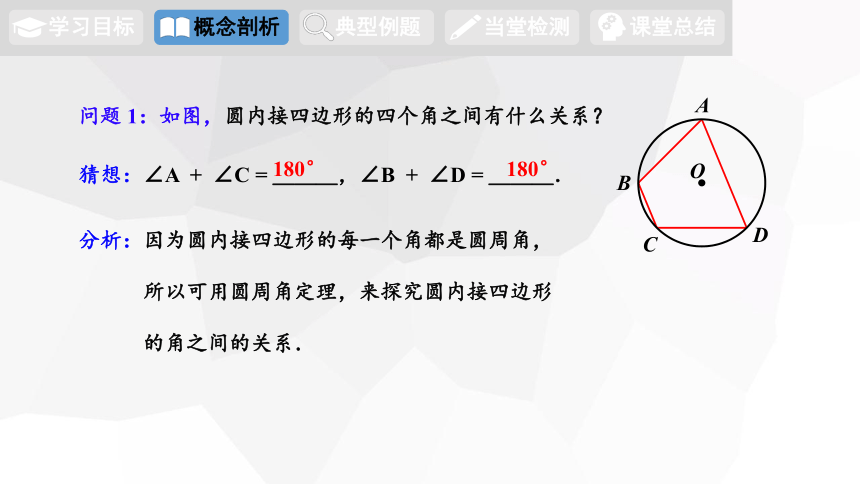
问题 1:如图,圆内接四边形的四个角之间有什么关系?
猜想:∠A + ∠C = ___,∠B + ∠D = ___.
180°
180°
分析:因为圆内接四边形的每一个角都是圆周角,
所以可用圆周角定理,来探究圆内接四边形
的角之间的关系.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
B
A
C
D
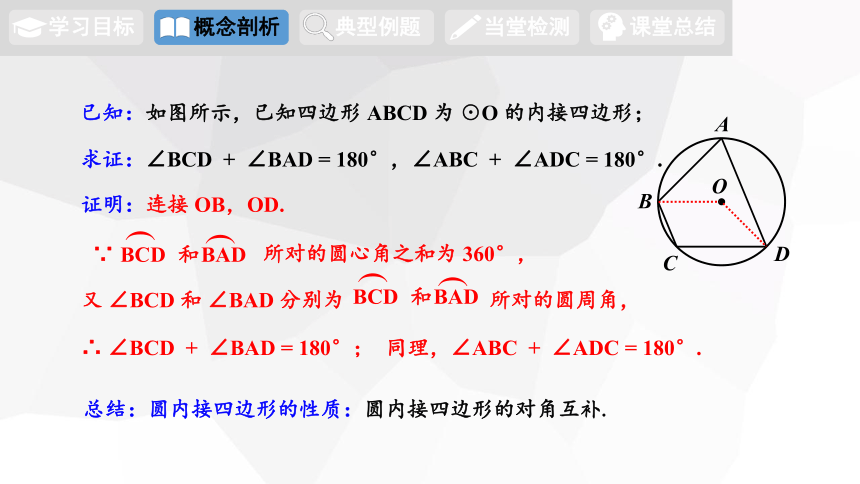
已知:如图所示,已知四边形 ABCD 为 ☉O 的内接四边形;
求证:∠BCD + ∠BAD = 180°,∠ABC + ∠ADC = 180°.
证明:连接 OB,OD.
∴ ∠BCD + ∠BAD = 180°;
同理,∠ABC + ∠ADC = 180°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
B
A
C
D
总结:圆内接四边形的性质:圆内接四边形的对角互补.
所对的圆心角之和为 360°,
BCD
(
BAD
(
和
∵
又 ∠BCD 和 ∠BAD 分别为 所对的圆周角,
BCD
(
BAD
(
和
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 1:如图所示,已知四边形 ABCD 为 ☉O 的内接四边形,∠ADE 为四边形 ABCD 的一个外角. 求证:∠ABC = ∠ADE.
(一)圆内接四边形的性质
解:∵ 四边形ABCD为☉O的内接四边形,
∴ ∠ABC + ∠ADC = 180°;
∵ ∠ADE + ∠ADC = 180°,
∴ ∠ABC = ∠ADE.
O
B
A
C
D
E
总结:圆内接四边形的推论:圆内接四边形的任一外角等于它的内对角.
归纳总结
圆内接四边形的角的“三种关系”:
(1)对角互补:若四边形 ABCD 为 ⊙O 的内接四边形,则:
∠A + ∠C = 180°,∠B + ∠D = 180°;
(2)四个角的和是360°:若四边形 ABCD 为 ⊙O 的内接四边形,则:
∠A + ∠B + ∠C + ∠D = 360°;
(3)圆内接四边形的任一外角等于它的内对角.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 如图,四边形 ABCD 是 ⊙O 的内接四边形,若 ∠BOD = 90°,则 ∠BCD 的度数是( )
A. 45° B. 90° C. 135° D. 150°
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.若 ABCD 为圆内接四边形,则下列选项可能成立的是 ( )
A. ∠A ∶ ∠B ∶ ∠C ∶ ∠D = 1 ∶ 2 ∶ 3 ∶ 4
B. ∠A ∶ ∠B ∶ ∠C ∶ ∠D = 2 ∶ 1 ∶ 3 ∶ 4
C. ∠A ∶ ∠B ∶ ∠C ∶ ∠D = 3 ∶ 2 ∶ 1 ∶ 4
D. ∠A ∶ ∠B ∶ ∠C ∶ ∠D = 4 ∶ 3 ∶ 3 ∶ 2
B
3. 如图所示,在圆内接四边形 ABCD 中,∠B = 30°,则∠D = .
150°
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
B
A
C
D
4. 在 ⊙O 中,∠CBD = 30°,∠BDC = 20°,求 ∠A.
O
A
B
D
C
解:∵ ∠CBD = 30°,∠BDC = 20°,
∴ ∠C = 180°- ∠CBD - ∠BDC = 130°;
∴ ∠A = 180°- ∠C = 50°;
(圆内接四边形对角互补)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5. 已知 ∠OAB = 40°,求 ∠C 的度数.
A
B
C
O
D
解:延长 AO 至 D,交圆心于点 D,连接 BD;
∵ ∠OAB = 40°且 AD 是直径,
∴ ∠ABD = 90°,∠D = 50°;
∴ ∠C = 180°– 50°= 130°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
方法总结:在此类题中要注意结合“直径所对的圆周角是直角”的知识点,并构造圆内接四边形来解题.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 圆内接多边形的定义:
一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆的内接
多边形,这个圆叫做这个多边形的外接圆;
2. 圆内接四边形的性质:
圆内接四边形的对角互补,且任何一个外角都等于它的内对角.
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角 第2课时
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.知道圆内接多边形和多边形的外接圆的定义;
2.能说出圆内接四边形的性质,并能灵活运用该性质解决问题.
复习导入:
问题 1:什么是圆周角?
概念:顶点在圆上,并且两边都和圆相交的角叫圆周角;
特征:① 角的顶点在圆上;
② 角的两边都与圆相交.
O
A
E
C
D
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
问题 2:什么是圆周角定理?
圆上一条弧所对的圆周角等于它所对的圆心角的一半.
即:∠BAC = ∠BOC.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
B
A
C
O
B
A
C
O
B
A
C
(一)圆内接四边形及其性质
圆内接四边形定义:如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
如图:
四边形 ABCD 为 ⊙ O 的内接四边形;
⊙ O 为四边形 ABCD 的外接圆.
O
B
A
C
D
问题 1:如图,圆内接四边形的四个角之间有什么关系?
猜想:∠A + ∠C = ___,∠B + ∠D = ___.
180°
180°
分析:因为圆内接四边形的每一个角都是圆周角,
所以可用圆周角定理,来探究圆内接四边形
的角之间的关系.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
B
A
C
D
已知:如图所示,已知四边形 ABCD 为 ☉O 的内接四边形;
求证:∠BCD + ∠BAD = 180°,∠ABC + ∠ADC = 180°.
证明:连接 OB,OD.
∴ ∠BCD + ∠BAD = 180°;
同理,∠ABC + ∠ADC = 180°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
B
A
C
D
总结:圆内接四边形的性质:圆内接四边形的对角互补.
所对的圆心角之和为 360°,
BCD
(
BAD
(
和
∵
又 ∠BCD 和 ∠BAD 分别为 所对的圆周角,
BCD
(
BAD
(
和
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 1:如图所示,已知四边形 ABCD 为 ☉O 的内接四边形,∠ADE 为四边形 ABCD 的一个外角. 求证:∠ABC = ∠ADE.
(一)圆内接四边形的性质
解:∵ 四边形ABCD为☉O的内接四边形,
∴ ∠ABC + ∠ADC = 180°;
∵ ∠ADE + ∠ADC = 180°,
∴ ∠ABC = ∠ADE.
O
B
A
C
D
E
总结:圆内接四边形的推论:圆内接四边形的任一外角等于它的内对角.
归纳总结
圆内接四边形的角的“三种关系”:
(1)对角互补:若四边形 ABCD 为 ⊙O 的内接四边形,则:
∠A + ∠C = 180°,∠B + ∠D = 180°;
(2)四个角的和是360°:若四边形 ABCD 为 ⊙O 的内接四边形,则:
∠A + ∠B + ∠C + ∠D = 360°;
(3)圆内接四边形的任一外角等于它的内对角.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 如图,四边形 ABCD 是 ⊙O 的内接四边形,若 ∠BOD = 90°,则 ∠BCD 的度数是( )
A. 45° B. 90° C. 135° D. 150°
C
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2.若 ABCD 为圆内接四边形,则下列选项可能成立的是 ( )
A. ∠A ∶ ∠B ∶ ∠C ∶ ∠D = 1 ∶ 2 ∶ 3 ∶ 4
B. ∠A ∶ ∠B ∶ ∠C ∶ ∠D = 2 ∶ 1 ∶ 3 ∶ 4
C. ∠A ∶ ∠B ∶ ∠C ∶ ∠D = 3 ∶ 2 ∶ 1 ∶ 4
D. ∠A ∶ ∠B ∶ ∠C ∶ ∠D = 4 ∶ 3 ∶ 3 ∶ 2
B
3. 如图所示,在圆内接四边形 ABCD 中,∠B = 30°,则∠D = .
150°
典型例题
当堂检测
学习目标
课堂总结
概念剖析
O
B
A
C
D
4. 在 ⊙O 中,∠CBD = 30°,∠BDC = 20°,求 ∠A.
O
A
B
D
C
解:∵ ∠CBD = 30°,∠BDC = 20°,
∴ ∠C = 180°- ∠CBD - ∠BDC = 130°;
∴ ∠A = 180°- ∠C = 50°;
(圆内接四边形对角互补)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
5. 已知 ∠OAB = 40°,求 ∠C 的度数.
A
B
C
O
D
解:延长 AO 至 D,交圆心于点 D,连接 BD;
∵ ∠OAB = 40°且 AD 是直径,
∴ ∠ABD = 90°,∠D = 50°;
∴ ∠C = 180°– 50°= 130°.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
方法总结:在此类题中要注意结合“直径所对的圆周角是直角”的知识点,并构造圆内接四边形来解题.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 圆内接多边形的定义:
一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆的内接
多边形,这个圆叫做这个多边形的外接圆;
2. 圆内接四边形的性质:
圆内接四边形的对角互补,且任何一个外角都等于它的内对角.
同课章节目录
