2.1整式 课件(共45张PPT) 2023-2024学年数学人教版七年级上册
文档属性
| 名称 | 2.1整式 课件(共45张PPT) 2023-2024学年数学人教版七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览











文档简介
(共45张PPT)
第二章 整式的加减
§2.1 整式(1)
学习目标:
(1)理解字母表示数的意义,会用含有字母的式子表示实际问题中的数量关系.
(2)经历用含有字母的式子表示实际问题的数量关系的过程,体会从具体到抽象的认识过程,发展符号意识.
学习重点:
理解字母表示数的意义,正确分析实际问题中的数量关系并用含有字母的式子表示数量关系,感受其中“抽象”的数学思想.
展示图片
青藏铁路上,在格尔木到拉萨之间有一段很长的冻土地段。列车在冻土地段的行驶速度是100千米/小时,在非冻土地段的行驶速度可以达到120千米小时。
请根据资料回答下面的问题:
列车在冻土地段行驶时,2小时能行驶多少千米?3小时呢?t小时呢?
青藏铁路创造的世界之最
注意:在含有字母的式子中若出现乘号,通常将乘号写作“ ”或
省略不写。如:100×a可以
写成100 a或100a。
解:它2小时行驶的路程是
100×2=200(千米)
3小时行驶的路程是
100×3=300(千米)
t小时行驶的路程是
100×t=100t(千米)
(1)苹果原价是每千克p元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是a cm,高是h cm,用式子表示它的体积;
(4)用式子表示数n的相反数.
例1
答案:(1) ;(2) ;(3) ;(4) .
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
例2
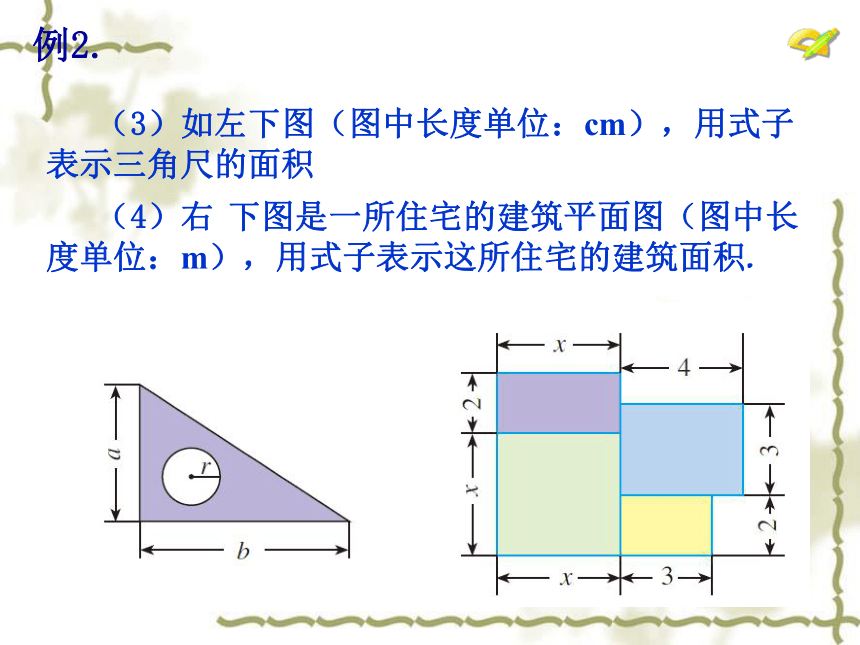
(3)如左下图(图中长度单位:cm),用式子表示三角尺的面积
(4)右 下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
例2.
解:
(3)三角尺的面积(单位:cm2 )是 .
(2)买3个篮球、5个排球、2个足球共需要
元.
(1)船在这条河中顺水行驶的速度是
km/h,逆水行驶的速度是 km/h.
(4)这所住宅的建筑面积(单位:m2)是
.
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们
之间的关系,如和、差、积、商及大、小、
多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳:
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,式子加括号.
归纳:
练习1(教科书第56页练习)
(1)某种商品每袋4.8元,在一个月内的销售量是m 袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体的体积.
(3)有两片棉田,一片有m hm2 (公顷,1 hm2 =104 m2 ),平均每公顷产棉花a kg;另一片有n hm2 ,平均每公顷产棉花b kg,用式子表示两片棉田上棉花的总产量.
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是a mm,小正方形的边长是b mm,用式子表示剩余部分的面积.
(1)5箱苹果重m kg,每箱重 kg ;
(2)一个数比a的2倍小5,则这个数为 ;
(3)全校学生总数是x,其中女生占总数52%,则女生人数是 ,男生人数是 ;
(4)某校前年购买计算机 x 台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,则学校三年共购买计算机 台;
(5)某班有a名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共 本;
(6)一个两位数,十位上的数字为a,个位上的数字为b,则这个两位数为 .
练习2 用式子表示:
小明房间的窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(他们的半径相同)。
(1)装饰物所占的面积是多少?
(2)窗户中能射进阳光部分的面积是多少?
b
a
2.如果数学书的每张纸长为a,宽为b,则纸张的面积和周长分别是____________
(ab、2a+2b)
1.一个塑料三角尺如图,阴影部分所占的面积是_________.
做一做
3.某校学生总数为x,其中男生人数占总数的 男生人数为________
做一做
做一做
4.一个长方体的底面是边长为a 的正方形,高是h ,则体积是________
a
a
h
(1)观察下列各式: , , , ,… ,
按此规律,第个 式子是 ;
例3
(2)测得一种树苗的高度与树苗生长的年数的有关数据如下表(树苗原高100cm),根据表格思考下面问题:
年数 高度/cm
1 100+5
2 100+10
3 100+15
4 100+20
…… ……
前四年树苗高度的变化与年数有什么关系?假设以后各年树苗高度的变化与年数保持上述关系,用式子表示生长了n年的树苗的高度.
例3
100+5×1
100+5×3
100+5×2
100+5×4
100+5×n
……
例3
(3)礼堂第1排有20个座位,后面每排
都比前一排多一个座位.用式子表示第 n
排的座位数.
用整式表示实际问题中的数量关系和变化规律,可以从特殊值入手,借助表格等分析,由特殊到一般,由个体到整体地观察、分析问题,发现规律,并用含有字母的式子表示一般的结论,这体现了抽象的数学思想.
先填空,再请说出你所列式子的运算含义。
1、边长为x的正方形的周长是 。
2、一辆汽车的速度是v千米/小时,行驶t小时所走过
的路程为 千米。
3、如图正方体的表面积为 ,体积为 。
4、设n表示一个数,则它的相反数是 .
a
4x
vt
a3
6a2
-n
挑战“记忆”
回顾 思考
知识的升华
我思,我进步
1
4 x
vt
a3
6a2
-n
数
字母
v×t
-1×n
像这样数与字母的积,这样的式子叫做单项式
-3x2y3
系数
指数和称次数
单项式中的数字因数叫做这个单项式的系数。
一个单项式中的所有字母的指数的和叫做这个单项式的次数。
如-3x的系数是_____,-ab的系数是_____
-3
-1
如-3x的次数是_____,ab的次数是_____
1
2
如 的系数是_____,
3
2
解剖单项式
-3x2y3
系数
指数和称次数
单项式 4x 6a2 a3 -n vt 2πR
系数
3 xy2z
2
1
4
6
1
-1
1
2π
2
7
x2yz
2
7
在研究单项式的系数问题时,要注意以下几点:
1.当单项式的系数是1或-1时,“1”通常省略不写。
2.圆周率π是常数。
3.当单项式的系数是带分数时,通常写成假分数。
4.单项式的系数应包括它前面的性质符号。
2
7
x2yz
单项式 4x 6a2 a3 -n vt 2πR
次数
在研究单项式的次数问题时,要注意以下两点:
1、在一个单项式中,所有字母的指数的和才叫做单项式的次数。
1
2
3
1
2
1
4
5
0
2、单独一个数的次数记为0。
比如 -3,0,m, 等都是单项式。
1.单独一个数或一个字母也叫单项式!
3.单项式的系数包含符号,当系数为1或-1时,这个“1”应省略不写。
2.单独一个非零数的次数是0。
比如-3的次数是0
00是没意义的
-3ab2的系数?
单项式的注意点
比如ab 、 -n
填空:
(1) 单项式-5y的系数是_____,次数是_____
(2) 单项式a3b的系数是_____,次数是_____
(3) 单项式 的系数是_____,次数是____
(4) 单项式 的系数是_____, 次数是____
-5
1
1
4
3
2
2
2
想好再举手
圆周率 是常数
1、判断下列各代数式是否是单项式。如不是,请说明理由;如是,请指出它的系数和次数。
①x+1; ② ; ③πr2; ④- a2b。
答:①不是,因为原代数式中出现了加法运算;
② 不是,因为原代数式是1与x的商;
③是,它的系数是π,次数是2;
④是,它的系数是- ,次数是3。
火眼金睛
火眼金睛
2、下面各题的判断是否正确。
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 。( )
×
×
×
×
×
√
1.填表:
单项式 2a2 -1.2h xy2 -t 2
系数
次数
2.用整式填空,指出单项式的次数:
(1)每包书有12册,n包书有( )册;
(2)底边为a,高为h的三角形面积为( );
成长的足迹
3. 单项式m2n2的系数_______,
次数是______, m2n2是____次单项式.
1
4
4
4.如果-5xym-1为4次单项式,则m=__.
4
5.若-ax2yb+1是关于x、y的五次单项式,且系数为-1/2,则a=____,b=____.
1/2
2
6.下列说法中,正确的是( )
D
成长的足迹
8、(1)买单价为a元的笔记本m本,付出20元,应找回_______元.
(20-am)
(2)用字母表示图形中的黑色部分面积是________
a
3
m
m
3a-m2
7、判断题:
(1)-5ab2的系数是5( )
(2)xy2的系数是0( )
(3) 的系数是 ( )
(4)-ab2c的次数是2( )
×
×
×
×
9.下列式子中哪些是单项式
规则:一个小组学生说出一个单项式,然后指定另一个小组的学生回答他的系数和次数;然后交换,看两小组哪一组回答得快而准。
游戏
想一想
下面两组式子各有什么特点?
(1) ,ab , ,
(2) ,2a+2b,
都是数与字母的乘积,
几个单项式的和
这样的代数式叫做单项
式(monomial).
叫做多项式(polynomial)
单项式
多项式
整式(integral expression)
单项式的次数(degree of monomial):一个单项式中,所有字母的指数之和.
多项式的次数:一个多项式中,次数最高的项的次数.
1次
2+1=3次
2次
2+1=3次
3.当单项式的系数为1或—1时,这个“1”应省略不写。
注意:
1.单独的一个数或一个字母也是单项式;
2.单独一个非零数的次数是0。
例1.下列式子中哪些是单项式,哪些是多项式
单项式:
多项式:x—y,
例2.下列说法中,正确的是( )
D
小红和小兰房间窗户的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径分别相同).
议一议
(1)窗户中能射进阳光的部分的面积分别是多少?(窗框面积忽略不计)
a
b
a
b
(2)你能指出其中的单项式或多项式吗?它们的次数分别是多少?
小红和小兰房间窗户的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径分别相同).
议一议
a
b
a
b
小结
整式
单项式
多项式
单项式、多项式的次数
作业
1,2,3
1.单项式m2n2的系数是_______,次数是______,m2n2是____次单项式.
2.多项式x+y-z是单项式___,___,___的和,它是___次___项式.
3.多项式3m3-2m-5+m2的常数项是____,二次项是_____,二次项的系数是_____.
4.如果 为4次单项式,则m=____.
练一练
回顾与反思
与你小组的其它成员交流一下,这节课你学到哪些知识?
强化与提高
1、已知 是关于 、 的三次单项式,那么 值是多少?
2、已知 是关于 、 的六次单项式,试求 的值。
作业:
课本第59页习题2.1的第1题
(要求再指出单项式的系数与次数)
第二章 整式的加减
§2.1 整式(1)
学习目标:
(1)理解字母表示数的意义,会用含有字母的式子表示实际问题中的数量关系.
(2)经历用含有字母的式子表示实际问题的数量关系的过程,体会从具体到抽象的认识过程,发展符号意识.
学习重点:
理解字母表示数的意义,正确分析实际问题中的数量关系并用含有字母的式子表示数量关系,感受其中“抽象”的数学思想.
展示图片
青藏铁路上,在格尔木到拉萨之间有一段很长的冻土地段。列车在冻土地段的行驶速度是100千米/小时,在非冻土地段的行驶速度可以达到120千米小时。
请根据资料回答下面的问题:
列车在冻土地段行驶时,2小时能行驶多少千米?3小时呢?t小时呢?
青藏铁路创造的世界之最
注意:在含有字母的式子中若出现乘号,通常将乘号写作“ ”或
省略不写。如:100×a可以
写成100 a或100a。
解:它2小时行驶的路程是
100×2=200(千米)
3小时行驶的路程是
100×3=300(千米)
t小时行驶的路程是
100×t=100t(千米)
(1)苹果原价是每千克p元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是a cm,高是h cm,用式子表示它的体积;
(4)用式子表示数n的相反数.
例1
答案:(1) ;(2) ;(3) ;(4) .
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
例2
(3)如左下图(图中长度单位:cm),用式子表示三角尺的面积
(4)右 下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
例2.
解:
(3)三角尺的面积(单位:cm2 )是 .
(2)买3个篮球、5个排球、2个足球共需要
元.
(1)船在这条河中顺水行驶的速度是
km/h,逆水行驶的速度是 km/h.
(4)这所住宅的建筑面积(单位:m2)是
.
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们
之间的关系,如和、差、积、商及大、小、
多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳:
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,式子加括号.
归纳:
练习1(教科书第56页练习)
(1)某种商品每袋4.8元,在一个月内的销售量是m 袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体的体积.
(3)有两片棉田,一片有m hm2 (公顷,1 hm2 =104 m2 ),平均每公顷产棉花a kg;另一片有n hm2 ,平均每公顷产棉花b kg,用式子表示两片棉田上棉花的总产量.
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是a mm,小正方形的边长是b mm,用式子表示剩余部分的面积.
(1)5箱苹果重m kg,每箱重 kg ;
(2)一个数比a的2倍小5,则这个数为 ;
(3)全校学生总数是x,其中女生占总数52%,则女生人数是 ,男生人数是 ;
(4)某校前年购买计算机 x 台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,则学校三年共购买计算机 台;
(5)某班有a名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共 本;
(6)一个两位数,十位上的数字为a,个位上的数字为b,则这个两位数为 .
练习2 用式子表示:
小明房间的窗户如图所示,其中上方的装饰物由两个四分之一圆和一个半圆组成(他们的半径相同)。
(1)装饰物所占的面积是多少?
(2)窗户中能射进阳光部分的面积是多少?
b
a
2.如果数学书的每张纸长为a,宽为b,则纸张的面积和周长分别是____________
(ab、2a+2b)
1.一个塑料三角尺如图,阴影部分所占的面积是_________.
做一做
3.某校学生总数为x,其中男生人数占总数的 男生人数为________
做一做
做一做
4.一个长方体的底面是边长为a 的正方形,高是h ,则体积是________
a
a
h
(1)观察下列各式: , , , ,… ,
按此规律,第个 式子是 ;
例3
(2)测得一种树苗的高度与树苗生长的年数的有关数据如下表(树苗原高100cm),根据表格思考下面问题:
年数 高度/cm
1 100+5
2 100+10
3 100+15
4 100+20
…… ……
前四年树苗高度的变化与年数有什么关系?假设以后各年树苗高度的变化与年数保持上述关系,用式子表示生长了n年的树苗的高度.
例3
100+5×1
100+5×3
100+5×2
100+5×4
100+5×n
……
例3
(3)礼堂第1排有20个座位,后面每排
都比前一排多一个座位.用式子表示第 n
排的座位数.
用整式表示实际问题中的数量关系和变化规律,可以从特殊值入手,借助表格等分析,由特殊到一般,由个体到整体地观察、分析问题,发现规律,并用含有字母的式子表示一般的结论,这体现了抽象的数学思想.
先填空,再请说出你所列式子的运算含义。
1、边长为x的正方形的周长是 。
2、一辆汽车的速度是v千米/小时,行驶t小时所走过
的路程为 千米。
3、如图正方体的表面积为 ,体积为 。
4、设n表示一个数,则它的相反数是 .
a
4x
vt
a3
6a2
-n
挑战“记忆”
回顾 思考
知识的升华
我思,我进步
1
4 x
vt
a3
6a2
-n
数
字母
v×t
-1×n
像这样数与字母的积,这样的式子叫做单项式
-3x2y3
系数
指数和称次数
单项式中的数字因数叫做这个单项式的系数。
一个单项式中的所有字母的指数的和叫做这个单项式的次数。
如-3x的系数是_____,-ab的系数是_____
-3
-1
如-3x的次数是_____,ab的次数是_____
1
2
如 的系数是_____,
3
2
解剖单项式
-3x2y3
系数
指数和称次数
单项式 4x 6a2 a3 -n vt 2πR
系数
3 xy2z
2
1
4
6
1
-1
1
2π
2
7
x2yz
2
7
在研究单项式的系数问题时,要注意以下几点:
1.当单项式的系数是1或-1时,“1”通常省略不写。
2.圆周率π是常数。
3.当单项式的系数是带分数时,通常写成假分数。
4.单项式的系数应包括它前面的性质符号。
2
7
x2yz
单项式 4x 6a2 a3 -n vt 2πR
次数
在研究单项式的次数问题时,要注意以下两点:
1、在一个单项式中,所有字母的指数的和才叫做单项式的次数。
1
2
3
1
2
1
4
5
0
2、单独一个数的次数记为0。
比如 -3,0,m, 等都是单项式。
1.单独一个数或一个字母也叫单项式!
3.单项式的系数包含符号,当系数为1或-1时,这个“1”应省略不写。
2.单独一个非零数的次数是0。
比如-3的次数是0
00是没意义的
-3ab2的系数?
单项式的注意点
比如ab 、 -n
填空:
(1) 单项式-5y的系数是_____,次数是_____
(2) 单项式a3b的系数是_____,次数是_____
(3) 单项式 的系数是_____,次数是____
(4) 单项式 的系数是_____, 次数是____
-5
1
1
4
3
2
2
2
想好再举手
圆周率 是常数
1、判断下列各代数式是否是单项式。如不是,请说明理由;如是,请指出它的系数和次数。
①x+1; ② ; ③πr2; ④- a2b。
答:①不是,因为原代数式中出现了加法运算;
② 不是,因为原代数式是1与x的商;
③是,它的系数是π,次数是2;
④是,它的系数是- ,次数是3。
火眼金睛
火眼金睛
2、下面各题的判断是否正确。
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 。( )
×
×
×
×
×
√
1.填表:
单项式 2a2 -1.2h xy2 -t 2
系数
次数
2.用整式填空,指出单项式的次数:
(1)每包书有12册,n包书有( )册;
(2)底边为a,高为h的三角形面积为( );
成长的足迹
3. 单项式m2n2的系数_______,
次数是______, m2n2是____次单项式.
1
4
4
4.如果-5xym-1为4次单项式,则m=__.
4
5.若-ax2yb+1是关于x、y的五次单项式,且系数为-1/2,则a=____,b=____.
1/2
2
6.下列说法中,正确的是( )
D
成长的足迹
8、(1)买单价为a元的笔记本m本,付出20元,应找回_______元.
(20-am)
(2)用字母表示图形中的黑色部分面积是________
a
3
m
m
3a-m2
7、判断题:
(1)-5ab2的系数是5( )
(2)xy2的系数是0( )
(3) 的系数是 ( )
(4)-ab2c的次数是2( )
×
×
×
×
9.下列式子中哪些是单项式
规则:一个小组学生说出一个单项式,然后指定另一个小组的学生回答他的系数和次数;然后交换,看两小组哪一组回答得快而准。
游戏
想一想
下面两组式子各有什么特点?
(1) ,ab , ,
(2) ,2a+2b,
都是数与字母的乘积,
几个单项式的和
这样的代数式叫做单项
式(monomial).
叫做多项式(polynomial)
单项式
多项式
整式(integral expression)
单项式的次数(degree of monomial):一个单项式中,所有字母的指数之和.
多项式的次数:一个多项式中,次数最高的项的次数.
1次
2+1=3次
2次
2+1=3次
3.当单项式的系数为1或—1时,这个“1”应省略不写。
注意:
1.单独的一个数或一个字母也是单项式;
2.单独一个非零数的次数是0。
例1.下列式子中哪些是单项式,哪些是多项式
单项式:
多项式:x—y,
例2.下列说法中,正确的是( )
D
小红和小兰房间窗户的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径分别相同).
议一议
(1)窗户中能射进阳光的部分的面积分别是多少?(窗框面积忽略不计)
a
b
a
b
(2)你能指出其中的单项式或多项式吗?它们的次数分别是多少?
小红和小兰房间窗户的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径分别相同).
议一议
a
b
a
b
小结
整式
单项式
多项式
单项式、多项式的次数
作业
1,2,3
1.单项式m2n2的系数是_______,次数是______,m2n2是____次单项式.
2.多项式x+y-z是单项式___,___,___的和,它是___次___项式.
3.多项式3m3-2m-5+m2的常数项是____,二次项是_____,二次项的系数是_____.
4.如果 为4次单项式,则m=____.
练一练
回顾与反思
与你小组的其它成员交流一下,这节课你学到哪些知识?
强化与提高
1、已知 是关于 、 的三次单项式,那么 值是多少?
2、已知 是关于 、 的六次单项式,试求 的值。
作业:
课本第59页习题2.1的第1题
(要求再指出单项式的系数与次数)
