24.1.1 圆 课件(共14张PPT) 2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 24.1.1 圆 课件(共14张PPT) 2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 11:25:13 | ||
图片预览




文档简介
(共14张PPT)
第二十四章 圆
24.1 圆的有关性质
24.1.1 圆
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.认识圆,理解圆的本质属性;
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆
有关的概念,并了解它们之间的区别和联系;(重点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
观察下图中的图形,试着列举更多生活中的例子.
(一)圆的有关概念
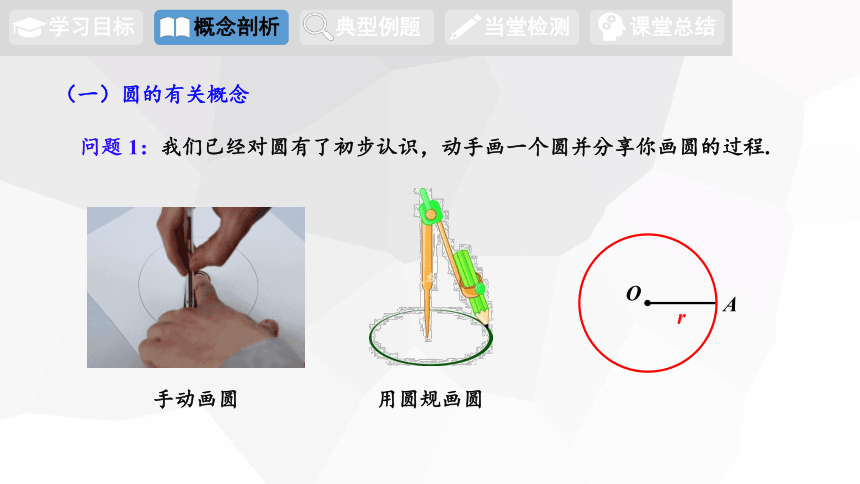
问题 1:我们已经对圆有了初步认识,动手画一个圆并分享你画圆的过程.
用圆规画圆
手动画圆
A
O
r
典型例题
当堂检测
学习目标
课堂总结
概念剖析
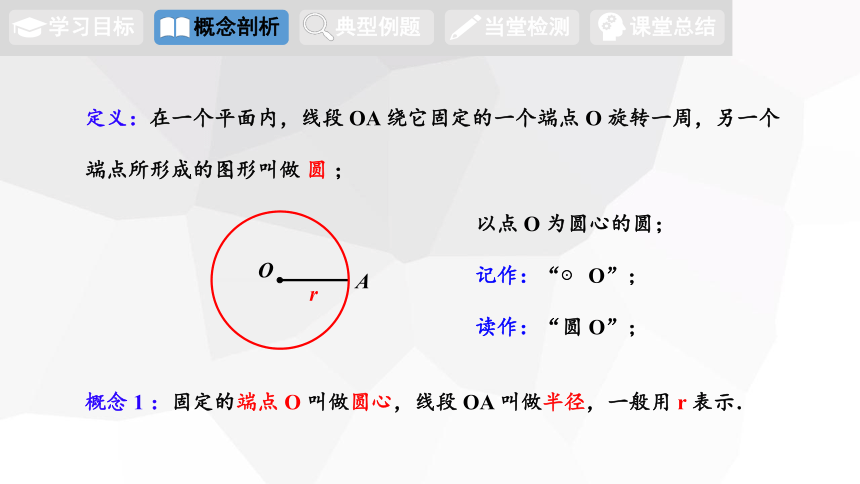
定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点所形成的图形叫做 圆 ;
概念 1 :固定的端点 O 叫做圆心,线段 OA 叫做半径,一般用 r 表示.
A
O
r
以点 O 为圆心的圆;
记作:“⊙ O”;
读作:“圆 O”;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
B
概念 2 :
弦:连接圆上任意两点的线段叫做弦;
直径:经过圆心的弦叫做直径.
图中 _________ 是弦,______是直径.
AB、AC
AC
归纳:直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
O
C
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
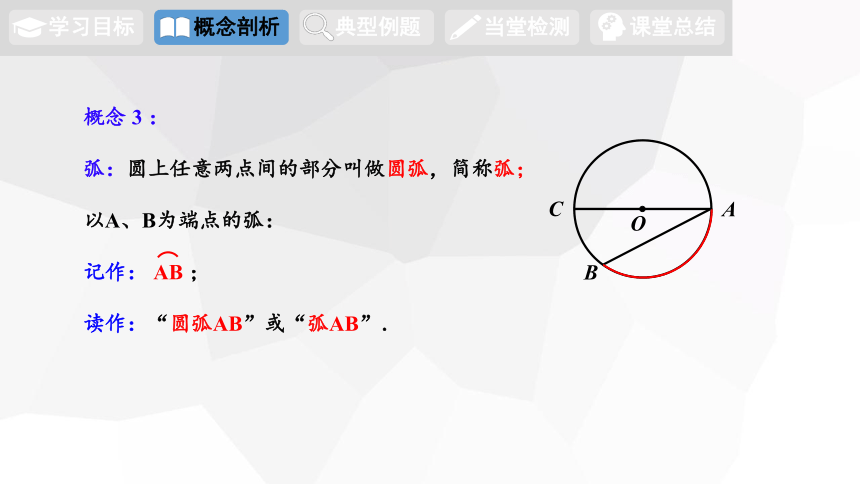
概念 3 :
弧:圆上任意两点间的部分叫做圆弧,简称弧;
以A、B为端点的弧:
记作: AB ;
读作:“圆弧AB”或“弧AB”.
B
O
C
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
概念 4 :
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆(如图中AC和ABC ).
劣弧:小于半圆的弧叫做劣弧,如图中的 AB ;
优弧:大于半圆的弧叫做优弧,如图中的ACB.
B
O
C
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
概念 5 :
同圆:能够重合的两个圆叫做等圆;
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.
归纳:半径相等的两个圆是等圆,同圆和等圆的半径相等.
O
r
O
r
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考:下面这两个图形有什么特点?
同心圆
等圆
确定一个圆的两个要素:一是圆心,二是半径;
结论:圆心确定圆的位置,半径确定圆的大小.
O
典型例题
当堂检测
学习目标
课堂总结
概念剖析
圆心相同,半径不同
半径相同,圆心不同
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 1:如图所示,O为圆心.
(1)写出图中所有的直径;
(2)写出图中所有的弦;
(3)写出以 A 为一个端点的所有弧.
(一)圆的有关概念
注意:凡直径都是弦,且是圆中最长的弦,但弦不一定是直径.
(2)弦有AB,AC,BD,BC;
解:(1)直径有AC,BD;
(3)以 A 为一个端点的所有弧有:
AB,ABC,ABD,AD,ADC,ADB
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 下列说法中,正确的是( )
① 弦是直径; ② 直径是弦;
③ 经过圆心的弦是直径; ④ 半圆是最长的弧;
⑤ 圆心相同,半径相等的两个圆是同心圆
A. ①②③ B. ②③ C. ②⑤ D. ③④⑤
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2. 如图,在正方形 ABCD 中,对角线 AC 和 BD 相交于点 O . 试说明点 A、B、C、D 在同一个圆上,并画出这个圆.
A
B
C
D
O
解:∵ 四边形 ABDC 是正方形,
∴ OA = OB = OC = OD;
即 A、B、C、D 在以点 O 为圆心、
OA 为半径的圆上.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 圆的有关概念:
弧
弦(半径):直径是圆中最长的弦;
定义
有关概念
劣弧
半圆:是特殊的弧;
优弧
圆
等圆
同圆
等弧:能够互相重合的两段弧
第二十四章 圆
24.1 圆的有关性质
24.1.1 圆
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1.认识圆,理解圆的本质属性;
2.认识弦、弧、半圆、优弧、劣弧、同心圆、等圆、等弧等与圆
有关的概念,并了解它们之间的区别和联系;(重点)
典型例题
当堂检测
学习目标
课堂总结
概念剖析
观察下图中的图形,试着列举更多生活中的例子.
(一)圆的有关概念
问题 1:我们已经对圆有了初步认识,动手画一个圆并分享你画圆的过程.
用圆规画圆
手动画圆
A
O
r
典型例题
当堂检测
学习目标
课堂总结
概念剖析
定义:在一个平面内,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点所形成的图形叫做 圆 ;
概念 1 :固定的端点 O 叫做圆心,线段 OA 叫做半径,一般用 r 表示.
A
O
r
以点 O 为圆心的圆;
记作:“⊙ O”;
读作:“圆 O”;
典型例题
当堂检测
学习目标
课堂总结
概念剖析
B
概念 2 :
弦:连接圆上任意两点的线段叫做弦;
直径:经过圆心的弦叫做直径.
图中 _________ 是弦,______是直径.
AB、AC
AC
归纳:直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
O
C
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
概念 3 :
弧:圆上任意两点间的部分叫做圆弧,简称弧;
以A、B为端点的弧:
记作: AB ;
读作:“圆弧AB”或“弧AB”.
B
O
C
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
概念 4 :
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆(如图中AC和ABC ).
劣弧:小于半圆的弧叫做劣弧,如图中的 AB ;
优弧:大于半圆的弧叫做优弧,如图中的ACB.
B
O
C
A
典型例题
当堂检测
学习目标
课堂总结
概念剖析
概念 5 :
同圆:能够重合的两个圆叫做等圆;
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.
归纳:半径相等的两个圆是等圆,同圆和等圆的半径相等.
O
r
O
r
典型例题
当堂检测
学习目标
课堂总结
概念剖析
思考:下面这两个图形有什么特点?
同心圆
等圆
确定一个圆的两个要素:一是圆心,二是半径;
结论:圆心确定圆的位置,半径确定圆的大小.
O
典型例题
当堂检测
学习目标
课堂总结
概念剖析
圆心相同,半径不同
半径相同,圆心不同
典型例题
当堂检测
学习目标
课堂总结
概念剖析
例 1:如图所示,O为圆心.
(1)写出图中所有的直径;
(2)写出图中所有的弦;
(3)写出以 A 为一个端点的所有弧.
(一)圆的有关概念
注意:凡直径都是弦,且是圆中最长的弦,但弦不一定是直径.
(2)弦有AB,AC,BD,BC;
解:(1)直径有AC,BD;
(3)以 A 为一个端点的所有弧有:
AB,ABC,ABD,AD,ADC,ADB
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 下列说法中,正确的是( )
① 弦是直径; ② 直径是弦;
③ 经过圆心的弦是直径; ④ 半圆是最长的弧;
⑤ 圆心相同,半径相等的两个圆是同心圆
A. ①②③ B. ②③ C. ②⑤ D. ③④⑤
B
典型例题
当堂检测
学习目标
课堂总结
概念剖析
2. 如图,在正方形 ABCD 中,对角线 AC 和 BD 相交于点 O . 试说明点 A、B、C、D 在同一个圆上,并画出这个圆.
A
B
C
D
O
解:∵ 四边形 ABDC 是正方形,
∴ OA = OB = OC = OD;
即 A、B、C、D 在以点 O 为圆心、
OA 为半径的圆上.
典型例题
当堂检测
学习目标
课堂总结
概念剖析
1. 圆的有关概念:
弧
弦(半径):直径是圆中最长的弦;
定义
有关概念
劣弧
半圆:是特殊的弧;
优弧
圆
等圆
同圆
等弧:能够互相重合的两段弧
同课章节目录
