第二十四章圆 复习课课件(共35张PPT)2023-2024学年人教版九年级数学上册
文档属性
| 名称 | 第二十四章圆 复习课课件(共35张PPT)2023-2024学年人教版九年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 915.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 11:35:55 | ||
图片预览







文档简介
(共35张PPT)
第二十四章 圆
复习课
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.会利用垂径定理及其推论进行计算和证明.
2.知道弧、弦、圆心角、圆周角之间的关系,并能应用它们之间的关系进行推理和证明.
3.知道点与圆的位置关系、直线与圆的位置关系,并能判断这些位置关系,知道切线的性质和判定定理及切线长定理,并能应用其进行推理和计算.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.会画三角形的外接圆和内切圆,知道三角形内心和外心的性质,知道圆内接多边形并会相关计算.
5.知道弧长和扇形面积的计算公式,并能用这些公式进行相关计算.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1
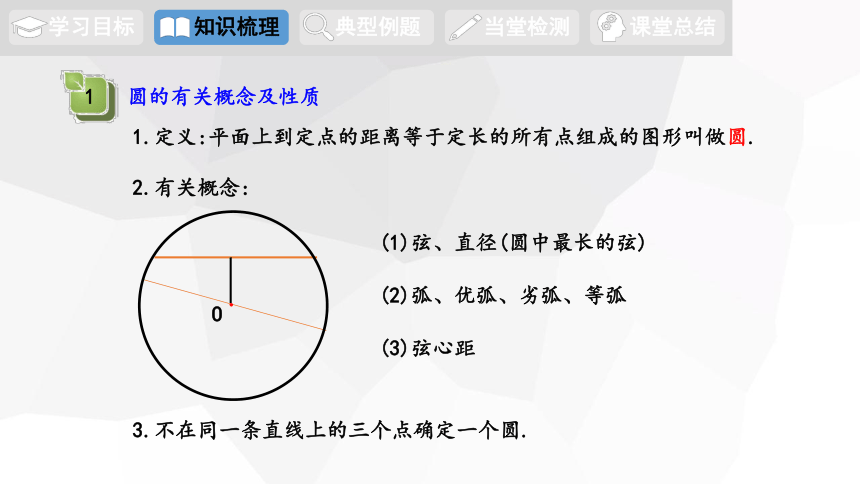
圆的有关概念及性质
1.定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆.
2.有关概念:
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
(3)弦心距
.
O
3.不在同一条直线上的三个点确定一个圆.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2
圆的对称性
1.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.
2.圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,即圆具有旋转不变性.
.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
4.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3
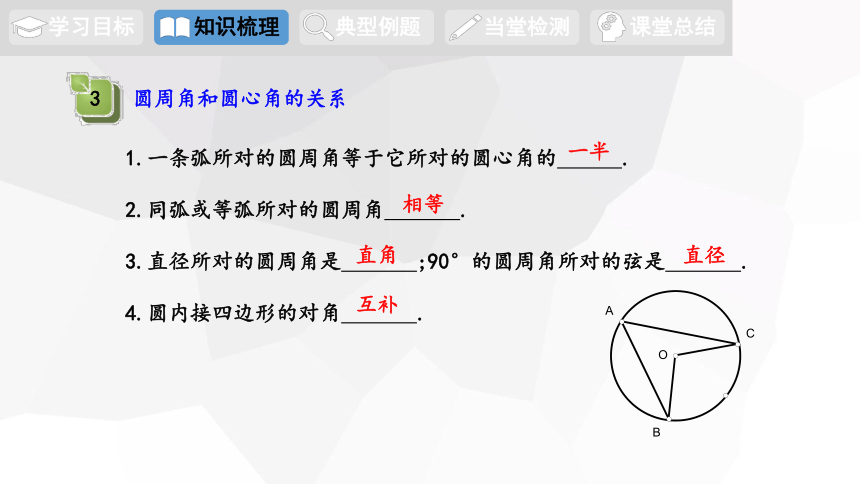
圆周角和圆心角的关系
1.一条弧所对的圆周角等于它所对的圆心角的 .
2.同弧或等弧所对的圆周角 .
3.直径所对的圆周角是 ;90°的圆周角所对的弦是 .
4.圆内接四边形的对角 .
一半
相等
直角
直径
互补
典型例题
当堂检测
学习目标
课堂总结
知识梳理
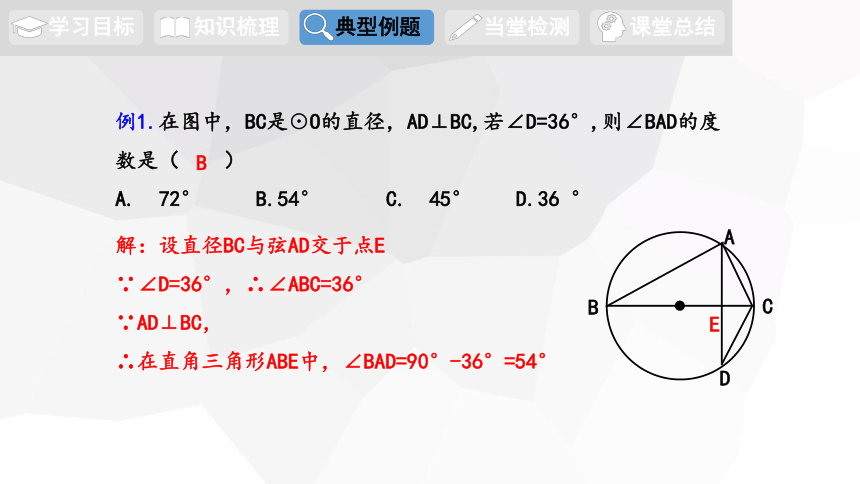
例1.在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )
A. 72° B.54° C. 45° D.36 °
A
B
C
D
B
解:设直径BC与弦AD交于点E
∵∠D=36°,∴∠ABC=36°
∵AD⊥BC,
∴在直角三角形ABE中,∠BAD=90°-36°=54°
E
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例2.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;(2)求证明:∠1=∠2.
解:(1)∵BC=DC,
∴∠CBD=∠CDB=39°,
∵∠BAC=∠CDB=39°, ∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°;
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,
而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠CBD,
∴∠1=∠2.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A
典型例题
当堂检测
学习目标
课堂总结
知识梳理
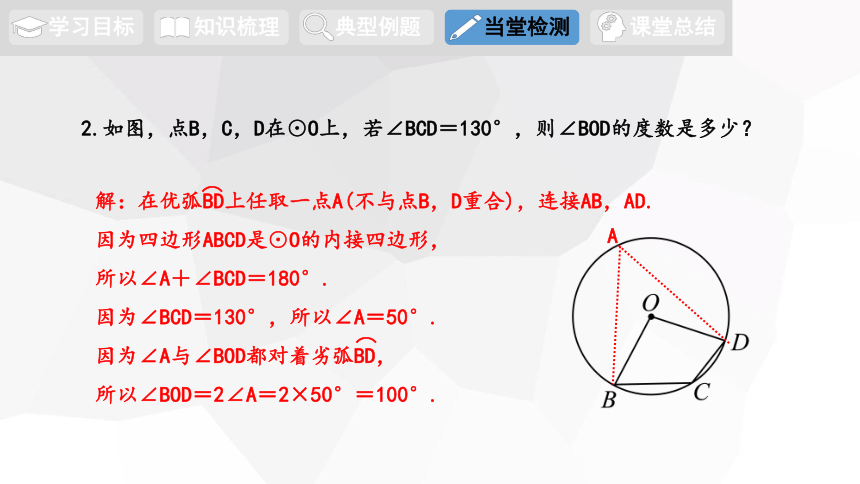
2.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是多少?
解:在优弧BD上任取一点A(不与点B,D重合),连接AB,AD.
因为四边形ABCD是⊙O的内接四边形,
所以∠A+∠BCD=180°.
因为∠BCD=130°,所以∠A=50°.
因为∠A与∠BOD都对着劣弧BD,
所以∠BOD=2∠A=2×50°=100°.
︵
︵
A
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4
垂径定理及推论
A
B
C
D
M└
③AM=BM,
若 ① CD是直径
② CD⊥AB
可推得
④AC=BC,
⌒
⌒
⑤AD=BD.
⌒
⌒
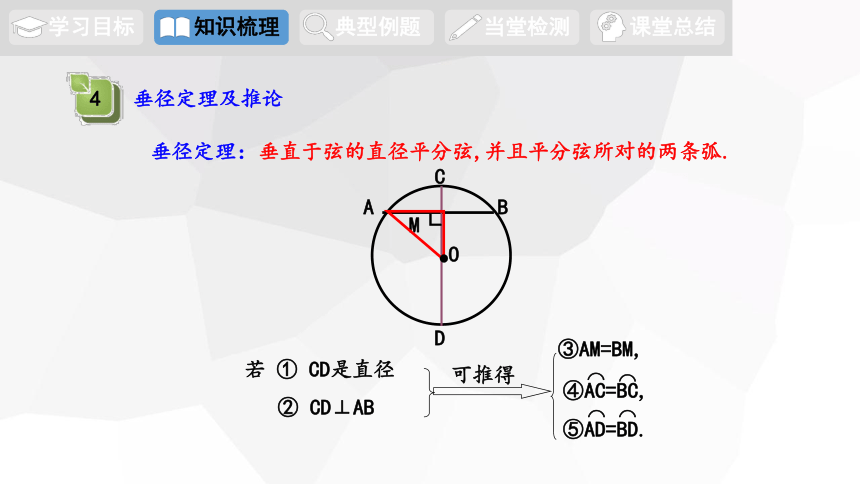
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
●O
典型例题
当堂检测
学习目标
课堂总结
知识梳理
②CD⊥AB,
由 ① CD是直径
③ AM=BM
可推得
④AC=BC,
⌒
⌒
⑤AD=BD.
⌒
⌒
●O
C
D
●
A
B
┗
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
M
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例3.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 mm.
8mm
A
B
8
C
D
O
解析:设圆心为O,连接AO,作出过点O的弓形高CD,垂足为D,可AO=5mm,OD=3mm
利用勾股定理进行计算,AD=4mm,
所以AB=8mm.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
A
O
B
C
E
F
3.如图,点C是扇形OAB上的AB的任意一点,OA=2,连接AC,BC,过点O作OE ⊥AC,OF ⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
(
典型例题
当堂检测
学习目标
课堂总结
知识梳理
●A
●B
●C
点与圆的位置关系 点到圆心的距离d与圆的半径r之间关系
点在圆外
点在圆上
点在圆内
●O
d
r
d﹥r
d=r
d﹤r
5
与圆的位置关系
1.点和圆的位置关系
典型例题
当堂检测
学习目标
课堂总结
知识梳理
直线与圆位的置关系 圆心与直线的距离d与圆的半径r的关系 直线名称
直线与圆的交点个数
相离
相切
相交
●
l
d
r
0
切线
d﹤r
割线
2
d﹥r
—
d=r
1
2.直线和圆的位置关系
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例4.2019年某企业将地处A,B两地的两个小厂合并成一个大工厂,为了方便A,B两地职工的联系,企业准备在相距2km的A,B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向,B地的西偏北45°方向的C处有一半径为0.7km的公园,问:修筑的这条公路会不会穿过公园?为什么?
解:过点C作CD⊥AB,垂足为D,
∵∠B=45°,∴∠BCD=45°,CD=BD.
设CD=x,则BD=x,
由∠A=30°知,AC=2x,AD
∴ x+x=2,即x= -1,即CD= -1≈0.732(km)>0.7km,
∴以C为圆心,0.7km为半径的圆与AB相离,即计划修筑的这条公路不会穿过公园.
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( )
A. r≥15 B. 15<r≤20
C. 15<r<25 D. 20≤r<25
C
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于点P,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( )
A. 3次 B. 5次 C. 6次 D. 7次
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.切线的判定一般有三种方法:
a.定义法:和圆有唯一的一个公共点
b.距离法: d=r
c.判定定理:过半径的外端且垂直于半径
6
切线的性质与判定
典型例题
当堂检测
学习目标
课堂总结
知识梳理
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
切线长:
从圆外一点引圆的切线,这个点与切点间的线段的长称为切线长.
2.切线长及切线长定理
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例5.如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.
(1)求证:∠1=∠BAD;(2)求证:BE是⊙O的切线.
证明:(1)∵BD=BA,∴∠BDA=∠BAD,
∵∠1=∠BDA,∴∠1=∠BAD;
(2)连接BO,∵∠ABC=90°,
又∵∠BAD+∠BCD=180°,∴∠BCO+∠BCD=180°,
∵OB=OC,∴∠BCO=∠CBO,∴∠CBO+∠BCD=180°,∴OB∥DE,
∵BE⊥DE,∴EB⊥OB,
∵OB是⊙O的半径,∴BE是⊙O的切线.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
6.如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
A.70° B.35°
C.20° D.40°
解:∵AC是圆O的切线,AB是圆O的直径,
∴AB⊥AC.∴∠CAB=90°.
又∵∠C=70°,∴∠CBA=20°
∴∠DOA=40°.故选:D.
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
7.如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM=AN;(2)若⊙O的半径R=3,PA=9,求OM的长.
解:(1)证明:连接OA,则OA⊥AP.∵MN⊥AP
∴MN∥OA.∵OM∥AP,∴四边形ANMO是矩形.∴OM=AN.
(2)连接OB,则OB⊥BP.∵OA=MN,OA=OB,OM∥AP,
∴OB=MN,∠OMB=∠NPM.∴Rt△OBM≌Rt△MNP,∴OM=MP,
设OM=x,则NP=9-x.
在Rt△MNP中,有x2=32+(9-x)2.∴x=5即OM=5.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
3.这个三角形叫做圆的外切三角形.
4.三角形的内心就是三角形的三个内角角平分线的交点.
F
┐
A
C
I
┐
┐
D
E
三角形的内心到三角形的三边的距离相等.
7
三角形的内切圆及内心
典型例题
当堂检测
学习目标
课堂总结
知识梳理
8
正多边形和圆
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
边心距
正多边形的边心距
计算公式:①正多边形的内角和=
②中心角=
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例6.如图,在正五边形ABCDE中,CA与DB相交于点F,若AB=1,求BF的长度.
解:在正五边形ABCDE中,
∵∠ABC=∠DCB=108°,BC=BA=CD,
∴∠BAC=∠BCA=∠CDB=∠CBD=36°,
∴∠ABF=72°,
∴∠AFB=∠CBD+∠ACB=72°,
∴∠AFB=∠ABF,∠FCB=∠FBC,
∴AF=AB=1,FB=CF,设FB=FC=x,
∵∠BCF=∠BCA,∠CBF=∠CAB,
∴△BCF∽△ACB,∴CB2=CF CA,
∴x(x+1)=1,
∴x= 或 (舍去),
∴BF= .
典型例题
当堂检测
学习目标
课堂总结
知识梳理
解:∵点I是△ABC的内心,
∴∠BAC=2∠IAC,∠ACB=2∠ICA,
∴∠B=180°-(∠BAC+∠ACB)
=180°-2(∠IAC+∠ICA)
=180°-2(180°-∠AIC)=68°.
又四边形ABCD内接于⊙O,∴∠CDE=∠B=68°.
8.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56° B.62° C.68° D.78°
C
典型例题
当堂检测
学习目标
课堂总结
知识梳理
9.如图,用八根长为4cm的铁丝,首尾相接围成一个正八边形(接点不固定)要将它的四边按图中的方式向内等距离移动acm,同时去掉另外四根长为4cm的铁丝(虚线部分)得到一个正方形,则a的值为( )
A.4cm B.2cm C. cm D. cm
C
典型例题
当堂检测
学习目标
课堂总结
知识梳理
10.如图,已知正六边形ABCDEF的边长为 ,点G,H,I,J,K,L依次在正六边形的六条边上,且AG=BH=CI=DJ=EK=FL,顺次连结G,I,K,和H,J,L,求图中阴影部分的周长C的取值范围.
解:根据对称性可知,△GKI,△HLJ是等边三角形.阴影部分是正六边形,边长为GK的 .
∵GK的最大值为3,GK的最小值为 ,
∴阴影部分的正六边形的边长的最大值为1,最小值为 ,
∴图中阴影部分的周长C的取值范围为:3 ≤C≤6.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
9
弧长及扇形的面积
(1)弧长公式:
(2)扇形面积公式:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例7.如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上, OA=1,∠AOC=120°,∠1=∠2,求扇形OEF的面积.
解:∵四边形OABC为菱形
∴OC=OA=1
∵ ∠AOC=120°,∠1=∠2
∴ ∠FOE=120°
又∵点C在以点O为圆心的圆上
典型例题
当堂检测
学习目标
课堂总结
知识梳理
11.如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为
∴正方形ABCD的边长为
典型例题
当堂检测
学习目标
课堂总结
知识梳理
圆
圆的有关性质
与圆有关的位置关系
与圆有关的计算
垂径定理
添加辅助线
连半径,作弦心距,构造直角三角形
圆周角定理
添加辅助线
作弦,构造直径所对的圆周角
点与圆的位置关系
点在圆环内:r <d <R
直线与圆的位置的关系
添加辅助
线证切线
有公共点,连半径,证垂直;无公共点,作垂直,证半径;见切点,连半径,得垂直.
正多边形和圆
转化
直角三角形
弧长和扇形
灵活使用公式
第二十四章 圆
复习课
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.会利用垂径定理及其推论进行计算和证明.
2.知道弧、弦、圆心角、圆周角之间的关系,并能应用它们之间的关系进行推理和证明.
3.知道点与圆的位置关系、直线与圆的位置关系,并能判断这些位置关系,知道切线的性质和判定定理及切线长定理,并能应用其进行推理和计算.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.会画三角形的外接圆和内切圆,知道三角形内心和外心的性质,知道圆内接多边形并会相关计算.
5.知道弧长和扇形面积的计算公式,并能用这些公式进行相关计算.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1
圆的有关概念及性质
1.定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆.
2.有关概念:
(1)弦、直径(圆中最长的弦)
(2)弧、优弧、劣弧、等弧
(3)弦心距
.
O
3.不在同一条直线上的三个点确定一个圆.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2
圆的对称性
1.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.
2.圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,即圆具有旋转不变性.
.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3.在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
4.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
3
圆周角和圆心角的关系
1.一条弧所对的圆周角等于它所对的圆心角的 .
2.同弧或等弧所对的圆周角 .
3.直径所对的圆周角是 ;90°的圆周角所对的弦是 .
4.圆内接四边形的对角 .
一半
相等
直角
直径
互补
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例1.在图中,BC是☉O的直径,AD⊥BC,若∠D=36°,则∠BAD的度数是( )
A. 72° B.54° C. 45° D.36 °
A
B
C
D
B
解:设直径BC与弦AD交于点E
∵∠D=36°,∴∠ABC=36°
∵AD⊥BC,
∴在直角三角形ABE中,∠BAD=90°-36°=54°
E
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例2.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
(1)若∠CBD=39°,求∠BAD的度数;(2)求证明:∠1=∠2.
解:(1)∵BC=DC,
∴∠CBD=∠CDB=39°,
∵∠BAC=∠CDB=39°, ∠CAD=∠CBD=39°,
∴∠BAD=∠BAC+∠CAD=39°+39°=78°;
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,
而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠CBD,
∴∠1=∠2.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A
典型例题
当堂检测
学习目标
课堂总结
知识梳理
2.如图,点B,C,D在⊙O上,若∠BCD=130°,则∠BOD的度数是多少?
解:在优弧BD上任取一点A(不与点B,D重合),连接AB,AD.
因为四边形ABCD是⊙O的内接四边形,
所以∠A+∠BCD=180°.
因为∠BCD=130°,所以∠A=50°.
因为∠A与∠BOD都对着劣弧BD,
所以∠BOD=2∠A=2×50°=100°.
︵
︵
A
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4
垂径定理及推论
A
B
C
D
M└
③AM=BM,
若 ① CD是直径
② CD⊥AB
可推得
④AC=BC,
⌒
⌒
⑤AD=BD.
⌒
⌒
垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
●O
典型例题
当堂检测
学习目标
课堂总结
知识梳理
②CD⊥AB,
由 ① CD是直径
③ AM=BM
可推得
④AC=BC,
⌒
⌒
⑤AD=BD.
⌒
⌒
●O
C
D
●
A
B
┗
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
M
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例3.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这个小圆孔的宽口AB的长度为 mm.
8mm
A
B
8
C
D
O
解析:设圆心为O,连接AO,作出过点O的弓形高CD,垂足为D,可AO=5mm,OD=3mm
利用勾股定理进行计算,AD=4mm,
所以AB=8mm.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
A
O
B
C
E
F
3.如图,点C是扇形OAB上的AB的任意一点,OA=2,连接AC,BC,过点O作OE ⊥AC,OF ⊥BC,垂足分别为E,F,连接EF,则EF的长度等于 .
(
典型例题
当堂检测
学习目标
课堂总结
知识梳理
●A
●B
●C
点与圆的位置关系 点到圆心的距离d与圆的半径r之间关系
点在圆外
点在圆上
点在圆内
●O
d
r
d﹥r
d=r
d﹤r
5
与圆的位置关系
1.点和圆的位置关系
典型例题
当堂检测
学习目标
课堂总结
知识梳理
直线与圆位的置关系 圆心与直线的距离d与圆的半径r的关系 直线名称
直线与圆的交点个数
相离
相切
相交
●
l
d
r
0
切线
d﹤r
割线
2
d﹥r
—
d=r
1
2.直线和圆的位置关系
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例4.2019年某企业将地处A,B两地的两个小厂合并成一个大工厂,为了方便A,B两地职工的联系,企业准备在相距2km的A,B两地之间修筑一条笔直公路(即图中的线段AB),经测量,在A地的北偏东60°方向,B地的西偏北45°方向的C处有一半径为0.7km的公园,问:修筑的这条公路会不会穿过公园?为什么?
解:过点C作CD⊥AB,垂足为D,
∵∠B=45°,∴∠BCD=45°,CD=BD.
设CD=x,则BD=x,
由∠A=30°知,AC=2x,AD
∴ x+x=2,即x= -1,即CD= -1≈0.732(km)>0.7km,
∴以C为圆心,0.7km为半径的圆与AB相离,即计划修筑的这条公路不会穿过公园.
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
4.已知矩形ABCD的边AB=15,BC=20,以点B为圆心作圆,使A,C,D三点至少有一点在⊙B内,且至少有一点在⊙B外,则⊙B的半径r的取值范围是( )
A. r≥15 B. 15<r≤20
C. 15<r<25 D. 20≤r<25
C
典型例题
当堂检测
学习目标
课堂总结
知识梳理
5.如图,⊙O1的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD的中心,O1O2垂直AB于点P,O1O2=8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1与正方形ABCD的边只有一个公共点的情况一共出现( )
A. 3次 B. 5次 C. 6次 D. 7次
B
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.切线的判定一般有三种方法:
a.定义法:和圆有唯一的一个公共点
b.距离法: d=r
c.判定定理:过半径的外端且垂直于半径
6
切线的性质与判定
典型例题
当堂检测
学习目标
课堂总结
知识梳理
切线长定理:
从圆外一点可以引圆的两条切线,它们的切线长相等.这一点和圆心的连线平分这两条切线的夹角.
切线长:
从圆外一点引圆的切线,这个点与切点间的线段的长称为切线长.
2.切线长及切线长定理
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例5.如图,⊙O是△ABC的外接圆,AC为直径,弦BD=BA,BE⊥DC交DC的延长线于点E.
(1)求证:∠1=∠BAD;(2)求证:BE是⊙O的切线.
证明:(1)∵BD=BA,∴∠BDA=∠BAD,
∵∠1=∠BDA,∴∠1=∠BAD;
(2)连接BO,∵∠ABC=90°,
又∵∠BAD+∠BCD=180°,∴∠BCO+∠BCD=180°,
∵OB=OC,∴∠BCO=∠CBO,∴∠CBO+∠BCD=180°,∴OB∥DE,
∵BE⊥DE,∴EB⊥OB,
∵OB是⊙O的半径,∴BE是⊙O的切线.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
6.如图,AB是⊙O的直径,AC切⊙O于A,BC交⊙O于点D,若∠C=70°,则∠AOD的度数为( )
A.70° B.35°
C.20° D.40°
解:∵AC是圆O的切线,AB是圆O的直径,
∴AB⊥AC.∴∠CAB=90°.
又∵∠C=70°,∴∠CBA=20°
∴∠DOA=40°.故选:D.
D
典型例题
当堂检测
学习目标
课堂总结
知识梳理
7.如图,PA,PB分别与⊙O相切于点A,B,点M在PB上,且OM∥AP,MN⊥AP,垂足为N.
(1)求证:OM=AN;(2)若⊙O的半径R=3,PA=9,求OM的长.
解:(1)证明:连接OA,则OA⊥AP.∵MN⊥AP
∴MN∥OA.∵OM∥AP,∴四边形ANMO是矩形.∴OM=AN.
(2)连接OB,则OB⊥BP.∵OA=MN,OA=OB,OM∥AP,
∴OB=MN,∠OMB=∠NPM.∴Rt△OBM≌Rt△MNP,∴OM=MP,
设OM=x,则NP=9-x.
在Rt△MNP中,有x2=32+(9-x)2.∴x=5即OM=5.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
1.与三角形各边都相切的圆叫做三角形的内切圆.
2.三角形内切圆的圆心叫做三角形的内心.
3.这个三角形叫做圆的外切三角形.
4.三角形的内心就是三角形的三个内角角平分线的交点.
F
┐
A
C
I
┐
┐
D
E
三角形的内心到三角形的三边的距离相等.
7
三角形的内切圆及内心
典型例题
当堂检测
学习目标
课堂总结
知识梳理
8
正多边形和圆
外接圆的圆心
正多边形的中心
外接圆的半径
正多边形的半径
每一条边所
对的圆心角
正多边形的中心角
边心距
正多边形的边心距
计算公式:①正多边形的内角和=
②中心角=
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例6.如图,在正五边形ABCDE中,CA与DB相交于点F,若AB=1,求BF的长度.
解:在正五边形ABCDE中,
∵∠ABC=∠DCB=108°,BC=BA=CD,
∴∠BAC=∠BCA=∠CDB=∠CBD=36°,
∴∠ABF=72°,
∴∠AFB=∠CBD+∠ACB=72°,
∴∠AFB=∠ABF,∠FCB=∠FBC,
∴AF=AB=1,FB=CF,设FB=FC=x,
∵∠BCF=∠BCA,∠CBF=∠CAB,
∴△BCF∽△ACB,∴CB2=CF CA,
∴x(x+1)=1,
∴x= 或 (舍去),
∴BF= .
典型例题
当堂检测
学习目标
课堂总结
知识梳理
解:∵点I是△ABC的内心,
∴∠BAC=2∠IAC,∠ACB=2∠ICA,
∴∠B=180°-(∠BAC+∠ACB)
=180°-2(∠IAC+∠ICA)
=180°-2(180°-∠AIC)=68°.
又四边形ABCD内接于⊙O,∴∠CDE=∠B=68°.
8.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
A.56° B.62° C.68° D.78°
C
典型例题
当堂检测
学习目标
课堂总结
知识梳理
9.如图,用八根长为4cm的铁丝,首尾相接围成一个正八边形(接点不固定)要将它的四边按图中的方式向内等距离移动acm,同时去掉另外四根长为4cm的铁丝(虚线部分)得到一个正方形,则a的值为( )
A.4cm B.2cm C. cm D. cm
C
典型例题
当堂检测
学习目标
课堂总结
知识梳理
10.如图,已知正六边形ABCDEF的边长为 ,点G,H,I,J,K,L依次在正六边形的六条边上,且AG=BH=CI=DJ=EK=FL,顺次连结G,I,K,和H,J,L,求图中阴影部分的周长C的取值范围.
解:根据对称性可知,△GKI,△HLJ是等边三角形.阴影部分是正六边形,边长为GK的 .
∵GK的最大值为3,GK的最小值为 ,
∴阴影部分的正六边形的边长的最大值为1,最小值为 ,
∴图中阴影部分的周长C的取值范围为:3 ≤C≤6.
典型例题
当堂检测
学习目标
课堂总结
知识梳理
9
弧长及扇形的面积
(1)弧长公式:
(2)扇形面积公式:
典型例题
当堂检测
学习目标
课堂总结
知识梳理
例7.如图,四边形OABC为菱形,点B、C在以点O为圆心的圆上, OA=1,∠AOC=120°,∠1=∠2,求扇形OEF的面积.
解:∵四边形OABC为菱形
∴OC=OA=1
∵ ∠AOC=120°,∠1=∠2
∴ ∠FOE=120°
又∵点C在以点O为圆心的圆上
典型例题
当堂检测
学习目标
课堂总结
知识梳理
11.如图,在正方形ABCD内有一条折线段,其中AE⊥EF,EF⊥FC,已知AE=6,EF=8,FC=10,求图中阴影部分的面积.
解:将线段FC平移到直线AE上,此时点F与点E重合,
点C到达点C'的位置.连接AC,如图所示.
根据平移的方法可知,四边形EFCC'是矩形.
∴ AC'=AE+EC'=AE+FC=16,CC'=EF=8.
在Rt△AC'C中,得
∴正方形ABCD外接圆的半径为
∴正方形ABCD的边长为
典型例题
当堂检测
学习目标
课堂总结
知识梳理
圆
圆的有关性质
与圆有关的位置关系
与圆有关的计算
垂径定理
添加辅助线
连半径,作弦心距,构造直角三角形
圆周角定理
添加辅助线
作弦,构造直径所对的圆周角
点与圆的位置关系
点在圆环内:r <d <R
直线与圆的位置的关系
添加辅助
线证切线
有公共点,连半径,证垂直;无公共点,作垂直,证半径;见切点,连半径,得垂直.
正多边形和圆
转化
直角三角形
弧长和扇形
灵活使用公式
同课章节目录
