第五章 《二元一次方程组》回顾与思考 课件(共19张PPT) 2023-2024学年北师大版八年级数学上册
文档属性
| 名称 | 第五章 《二元一次方程组》回顾与思考 课件(共19张PPT) 2023-2024学年北师大版八年级数学上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 17.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 11:27:55 | ||
图片预览






文档简介
(共19张PPT)
北师大版(2012)八年级数学(上)
第五章《二元一次方程组》
回顾与思考
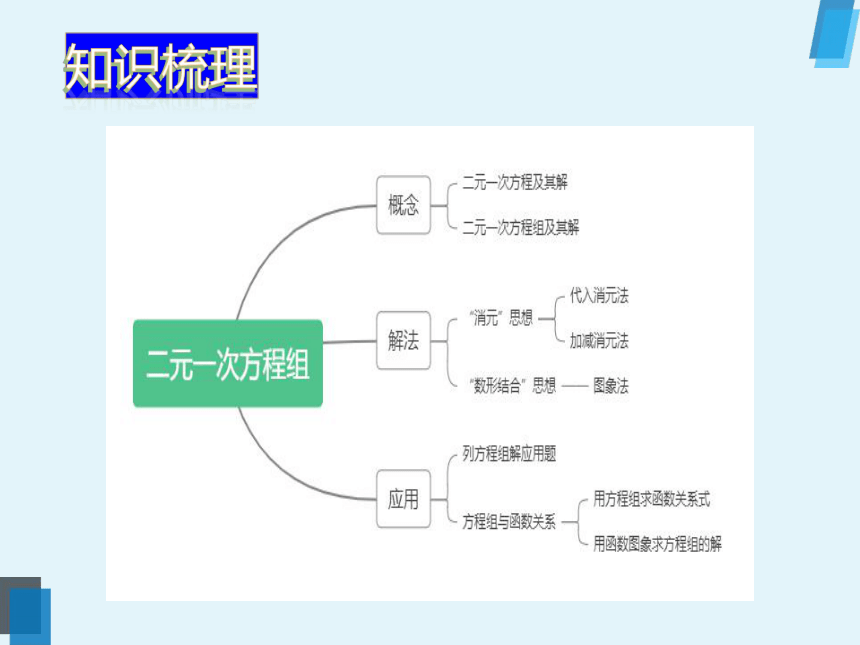
知识梳理
1、理解二元一次方程(组)及其解的概念;
2、会熟练解二元一次方程组,掌握二元一次方程(组)与一次函数的关系;
3、会用二元一次方程组分析解决实际问题。
1、二元一次方程组的解法;
2、用二元一次方程组分析解决实际问题。
综合应用二元一次方程组、一次函数知识分析解决实际问题。
学习目标
学习难点
学习重点
一、基本概念
(1)二元一次方程:含有 个未知数,并且所含未知数的 的次数都是 的方程.
二元一次方程的一个解:适合二元一次方程的 组未知数的值叫做这个二元一次方程的一个解.
(2)二元一次方程组:共含有 个未知数的二个 次方程所组成的一组方程叫做二元一次方程组.
二元一次方程组的解:二元一次方程组里各个方程的 解,叫做这个方程组的解.
两
1
一
两
一
公共
练一练
1、已知 是二元一次方程,
则m= ;
2、已知是 方程2ax-3y=11的解,
则a= ;
y=-3
x=1
3、已知是 方程组 的解,
则代数式(a+b)(a-b)的值为 .
y=-1
x=1
ax-by=-2
ax+by=3
-2
1
-6
例1: 解方程组:
二、二元一次方程组的解法
7x-3y=20
2x-y=5
①
②
解法1:代入消元法
由①得:y=2x-5③
将③代入②得:7x-3(2x-5)=20,解得x=5
把x=5代入③得:y=5
所以,方程组得解为
y=5
x=5
例:解方程组:
7x-3y=20
2x-y=5
①
②
解法2:加减消元法
由①×3得:6x-3y=15③
由②-③得:x=5
把x=5代入①,解得:y=5
所以,方程组得解为
y=5
x=5
解下列方程组:
练一练
5(y-1)=3(x+5)
3(x-1)=y+5
(2)
3x-2y=8
x+3y=-1
(1)
(3)
y=-1
x=2
y=7
x=5
y=1
x=1
三、二元一次方程组的应用
1、利用方程组求一次函数的关系
例 2:已知:一次函数的图象经过点A(0,1.5)和B(2,-3),与x轴相较于点C
(1)求它的函数关系式;
(2)求 AOC的面积。
C
B
A
(1)解:设函数关系式为:y=kx+b(k≠0)
∵图象经过点(0,1.5),(2,-3)
k×0+b=1.5
∴ k×2+b=-3
解得:k=-2.25, b=1.5
∴y=-2.25x+1.5
(2)在y=-2.25x+1.5中,令y=0,得x=2/3,C(2/3,0)
如图,一次函数y=kx+b图象与x轴的交点为(2,0),与一次函数y=x+n的图像的交点为(1,3)
(1)求k,b,n的值
(2)方程组:
的解为 。
y=kx+b
y=x+n
y=kx+b
y-x=n
x=1
y=3
练一练
(1)解:∵y=kx+b图象经过点(2,0),(1,3)
k×2+b=0
∴ k×1+b=3
解得:k=-3, b=6
代(1,3)入y=x+n中,得n=2
例3:《九章算术》卷八方程第十题原文为:“今有甲、乙二人持钱不知其数. 甲得乙半而钱五十,乙得甲太半面亦钱五十. 问:甲、乙持钱各几何?”题目大意是:
甲、乙两人各带了若干钱 如果甲得到乙所有钱的一半,
那么甲共有钱50;如果乙得到甲所有钱的三分之二 ,那么乙也共有钱50.问:甲、乙两人各带了多少钱?
2、列方程组解应用题
解:设甲、乙两人持钱的数量分别为x,y,
则可列方程组为:
解得:
y=25
x=37.5
答:甲持钱37.5,乙持钱25.
例4:2023 年 7 月 28 日至 8 月 8 日,第 31 届世界大学生运动会将在成都举行. “ 当好东道主, 热情迎嘉宾”,成都 某知名小吃店计划购买 A ,B 两种食材制作小吃. 已知购买 1 千克 A 种食材和 1 千克 B 种食材共需 68 元,购买 5 千克 A 种食材和 3 千克 B 种食材共需 280 元.
(1)求 A ,B 两种食材的单价;
(2)该小吃店计划购买两种食材共 36 千克,其中购买 A 种食材千克数不少于 B 种食材千克数的 2 倍,当 A,B 两种食材分别购买多少千克时,总费用最少?并求出最少总费用.
解:(1)设A种食材单价为x元/千克,B种食材单价为元y/千克,据题意可得
方程组:
x+y=68
5x+3y=280
解得:
y=30
x=38
所以,A种食材单价为38元/千克,B种食材单价为元30/千克
(2)设购买A种食材千克,则购买B种食材(36-a)千克,总费用为W元,据题意得:
W=38a+30(36-a)=8a+1080
由a≥2(36-a),得24≤a<36
所以,当a=24时,W最少=8×24+1080=1272(元)
1、中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有x个,甜果有y个,
则可列方程组为:
。
练一练
2、甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了________h.
(2)求线段DE对应的函数表达式.
(3)求轿车从甲地出发后经过多长时间追上货车.
1.5
(3)解:易求线段OA的表达式为:y=60x
y=60x
y=110x-195
解得:x=3.9,则3.9-1=2.9(小时)
∴轿车从甲地出发后经过2.9小时追上货车.
(2)解:设线段DE对应的函数表达式
y=kx+b ∵ 图象经过点(2.5,80),(4.5,300)
k×2.5+b=80
∴ k×4.5+b=300
解得:k=110, b=-195
∴y=110x-195
当堂检测
1、方程2x+y=5的正整数解有: 。
4x+y=12 x=
2、小明求得方程组 的解为
3x-2y= y=4
由于不小心,滴上了墨水,刚好遮住了两个数 和 ,则这两个数分别为( )
A、-2和2 B、-2和4 C、2和-4 D、2和-2
3、已知:
则以a,b为边长的等腰三角形的周长为: 。
x=2
y=1
x=1
y=3
D
10
4.已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨,某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运转,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计,有几种租车方案?
(3)若A型车、B型车每辆需租金分别为100元次、120元次,请选出最省钱的租车方案,并求出最少租车费.
2x+y=10
x+2y=11
解得:
y=4
x=3
解:(1)设1辆A型车和1辆B型车都装满货物一次可分别运货x吨,y吨,据题意得方程组:
(2)因3a+4b=31的正整数解有:
a=1
b=7
a=5
b=4
a=9
b=1
所以,共有3种方案。
(3)设总费用为W元,据题意得:W=100a+120(31-a)=-20a+3720
因为k=-20<0,W随a的增大而减小,
所以,当a=9时,W最少=-20×9+3720=3540(元)
5、如图,直线l1的解析式为y=-3x+3,且与x轴交于点D,直线l2经过点A(4,0),直线l1、l2交于点B.
(1)求点的坐标;
(2)求直线l2的解析表达式;
(3)求 ADC的面积;
(4)在直线l2上存在异于点C的另一点p,
使得 ADP与 ADC的面积相等,请直接写出点的坐标.
l1
l2
x
y
D
O
3
B
C
A
(4,0)
-1.5
解:(1)令y=0得:-3x+3=0,解得x=1
∴D(1,0)
(2)设解析式为y=kx+b(k≠0),
代入A(4,0),B(3,-1.5)得:
4k+b=0
3k+b=-1.5
解得:k=1.5,b=-6
∴y=1.5x-6
(3) y=1.5x-6 x=2
解方程组: 得
y=-3x+3 y=-3
∴C(2,-3)
∴S ADC=0.5×(3-1)×3=3
y=3
(4)P(6,3)
课堂小结
实际问题
二元一次方程
二元一次方程组
解法
应用
实际问题
作业布置
必做题:教材132-133页:第2,6,9,11题
选做题:教材134页:第15-20题
北师大版(2012)八年级数学(上)
第五章《二元一次方程组》
回顾与思考
知识梳理
1、理解二元一次方程(组)及其解的概念;
2、会熟练解二元一次方程组,掌握二元一次方程(组)与一次函数的关系;
3、会用二元一次方程组分析解决实际问题。
1、二元一次方程组的解法;
2、用二元一次方程组分析解决实际问题。
综合应用二元一次方程组、一次函数知识分析解决实际问题。
学习目标
学习难点
学习重点
一、基本概念
(1)二元一次方程:含有 个未知数,并且所含未知数的 的次数都是 的方程.
二元一次方程的一个解:适合二元一次方程的 组未知数的值叫做这个二元一次方程的一个解.
(2)二元一次方程组:共含有 个未知数的二个 次方程所组成的一组方程叫做二元一次方程组.
二元一次方程组的解:二元一次方程组里各个方程的 解,叫做这个方程组的解.
两
1
一
两
一
公共
练一练
1、已知 是二元一次方程,
则m= ;
2、已知是 方程2ax-3y=11的解,
则a= ;
y=-3
x=1
3、已知是 方程组 的解,
则代数式(a+b)(a-b)的值为 .
y=-1
x=1
ax-by=-2
ax+by=3
-2
1
-6
例1: 解方程组:
二、二元一次方程组的解法
7x-3y=20
2x-y=5
①
②
解法1:代入消元法
由①得:y=2x-5③
将③代入②得:7x-3(2x-5)=20,解得x=5
把x=5代入③得:y=5
所以,方程组得解为
y=5
x=5
例:解方程组:
7x-3y=20
2x-y=5
①
②
解法2:加减消元法
由①×3得:6x-3y=15③
由②-③得:x=5
把x=5代入①,解得:y=5
所以,方程组得解为
y=5
x=5
解下列方程组:
练一练
5(y-1)=3(x+5)
3(x-1)=y+5
(2)
3x-2y=8
x+3y=-1
(1)
(3)
y=-1
x=2
y=7
x=5
y=1
x=1
三、二元一次方程组的应用
1、利用方程组求一次函数的关系
例 2:已知:一次函数的图象经过点A(0,1.5)和B(2,-3),与x轴相较于点C
(1)求它的函数关系式;
(2)求 AOC的面积。
C
B
A
(1)解:设函数关系式为:y=kx+b(k≠0)
∵图象经过点(0,1.5),(2,-3)
k×0+b=1.5
∴ k×2+b=-3
解得:k=-2.25, b=1.5
∴y=-2.25x+1.5
(2)在y=-2.25x+1.5中,令y=0,得x=2/3,C(2/3,0)
如图,一次函数y=kx+b图象与x轴的交点为(2,0),与一次函数y=x+n的图像的交点为(1,3)
(1)求k,b,n的值
(2)方程组:
的解为 。
y=kx+b
y=x+n
y=kx+b
y-x=n
x=1
y=3
练一练
(1)解:∵y=kx+b图象经过点(2,0),(1,3)
k×2+b=0
∴ k×1+b=3
解得:k=-3, b=6
代(1,3)入y=x+n中,得n=2
例3:《九章算术》卷八方程第十题原文为:“今有甲、乙二人持钱不知其数. 甲得乙半而钱五十,乙得甲太半面亦钱五十. 问:甲、乙持钱各几何?”题目大意是:
甲、乙两人各带了若干钱 如果甲得到乙所有钱的一半,
那么甲共有钱50;如果乙得到甲所有钱的三分之二 ,那么乙也共有钱50.问:甲、乙两人各带了多少钱?
2、列方程组解应用题
解:设甲、乙两人持钱的数量分别为x,y,
则可列方程组为:
解得:
y=25
x=37.5
答:甲持钱37.5,乙持钱25.
例4:2023 年 7 月 28 日至 8 月 8 日,第 31 届世界大学生运动会将在成都举行. “ 当好东道主, 热情迎嘉宾”,成都 某知名小吃店计划购买 A ,B 两种食材制作小吃. 已知购买 1 千克 A 种食材和 1 千克 B 种食材共需 68 元,购买 5 千克 A 种食材和 3 千克 B 种食材共需 280 元.
(1)求 A ,B 两种食材的单价;
(2)该小吃店计划购买两种食材共 36 千克,其中购买 A 种食材千克数不少于 B 种食材千克数的 2 倍,当 A,B 两种食材分别购买多少千克时,总费用最少?并求出最少总费用.
解:(1)设A种食材单价为x元/千克,B种食材单价为元y/千克,据题意可得
方程组:
x+y=68
5x+3y=280
解得:
y=30
x=38
所以,A种食材单价为38元/千克,B种食材单价为元30/千克
(2)设购买A种食材千克,则购买B种食材(36-a)千克,总费用为W元,据题意得:
W=38a+30(36-a)=8a+1080
由a≥2(36-a),得24≤a<36
所以,当a=24时,W最少=8×24+1080=1272(元)
1、中国古代数学著作《算法统宗》中记载了这样一个题目:九百九十九文钱,甜果苦果买一千,四文钱买苦果七,十一文钱九个甜,甜苦两果各几个?其大意是:用九百九十九文钱共买了一千个苦果和甜果,其中四文钱可以买苦果七个,十一文钱可以买甜果九个.问:苦、甜果各有几个?设苦果有x个,甜果有y个,
则可列方程组为:
。
练一练
2、甲、乙两地距离300km,一辆货车和一辆轿车先后从甲地出发驶向乙地.如图,线段OA表示货车离甲地的距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地的距离y(km)与时间x(h)之间的函数关系,根据图象,解答下列问题:
(1)线段CD表示轿车在途中停留了________h.
(2)求线段DE对应的函数表达式.
(3)求轿车从甲地出发后经过多长时间追上货车.
1.5
(3)解:易求线段OA的表达式为:y=60x
y=60x
y=110x-195
解得:x=3.9,则3.9-1=2.9(小时)
∴轿车从甲地出发后经过2.9小时追上货车.
(2)解:设线段DE对应的函数表达式
y=kx+b ∵ 图象经过点(2.5,80),(4.5,300)
k×2.5+b=80
∴ k×4.5+b=300
解得:k=110, b=-195
∴y=110x-195
当堂检测
1、方程2x+y=5的正整数解有: 。
4x+y=12 x=
2、小明求得方程组 的解为
3x-2y= y=4
由于不小心,滴上了墨水,刚好遮住了两个数 和 ,则这两个数分别为( )
A、-2和2 B、-2和4 C、2和-4 D、2和-2
3、已知:
则以a,b为边长的等腰三角形的周长为: 。
x=2
y=1
x=1
y=3
D
10
4.已知:用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨,某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运转,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计,有几种租车方案?
(3)若A型车、B型车每辆需租金分别为100元次、120元次,请选出最省钱的租车方案,并求出最少租车费.
2x+y=10
x+2y=11
解得:
y=4
x=3
解:(1)设1辆A型车和1辆B型车都装满货物一次可分别运货x吨,y吨,据题意得方程组:
(2)因3a+4b=31的正整数解有:
a=1
b=7
a=5
b=4
a=9
b=1
所以,共有3种方案。
(3)设总费用为W元,据题意得:W=100a+120(31-a)=-20a+3720
因为k=-20<0,W随a的增大而减小,
所以,当a=9时,W最少=-20×9+3720=3540(元)
5、如图,直线l1的解析式为y=-3x+3,且与x轴交于点D,直线l2经过点A(4,0),直线l1、l2交于点B.
(1)求点的坐标;
(2)求直线l2的解析表达式;
(3)求 ADC的面积;
(4)在直线l2上存在异于点C的另一点p,
使得 ADP与 ADC的面积相等,请直接写出点的坐标.
l1
l2
x
y
D
O
3
B
C
A
(4,0)
-1.5
解:(1)令y=0得:-3x+3=0,解得x=1
∴D(1,0)
(2)设解析式为y=kx+b(k≠0),
代入A(4,0),B(3,-1.5)得:
4k+b=0
3k+b=-1.5
解得:k=1.5,b=-6
∴y=1.5x-6
(3) y=1.5x-6 x=2
解方程组: 得
y=-3x+3 y=-3
∴C(2,-3)
∴S ADC=0.5×(3-1)×3=3
y=3
(4)P(6,3)
课堂小结
实际问题
二元一次方程
二元一次方程组
解法
应用
实际问题
作业布置
必做题:教材132-133页:第2,6,9,11题
选做题:教材134页:第15-20题
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
