等腰三角形的性质
图片预览



文档简介
课件19张PPT。12.3.1等腰三角形把三角形按边的关系分类:复习回顾12.3.1等腰三角形等腰三角形的定义
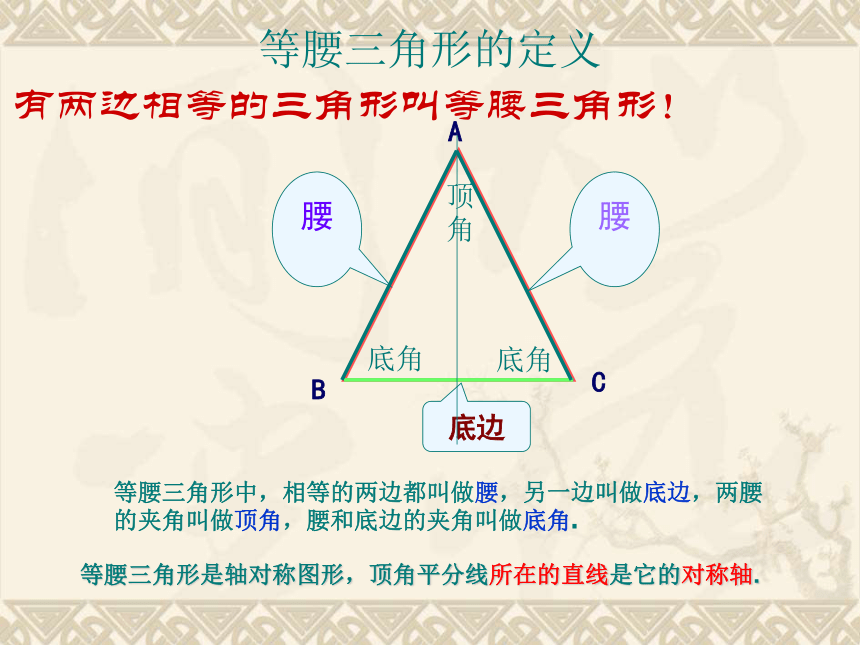
底边底角底角顶角等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两边相等的三角形叫等腰三角形!
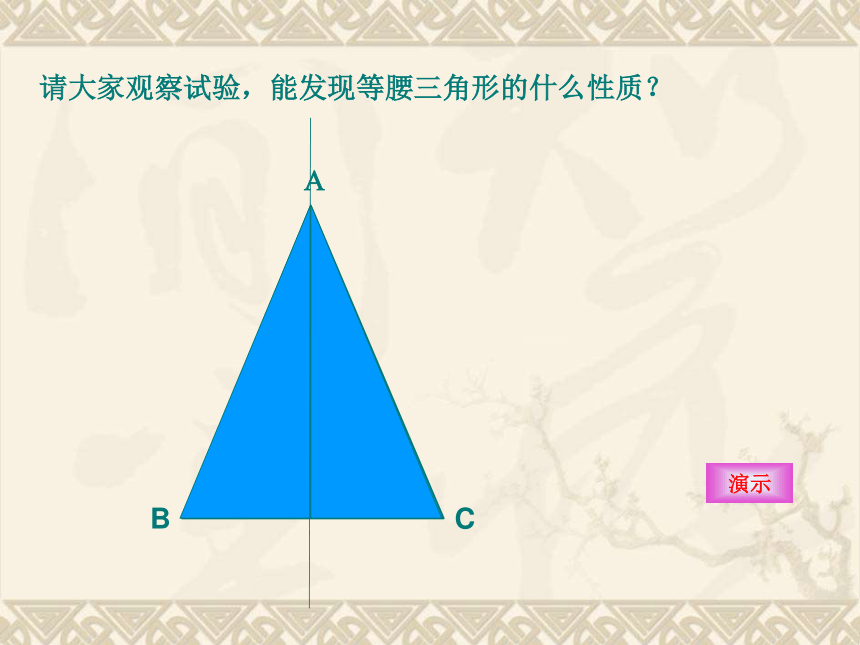
等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴.请大家观察试验,能发现等腰三角形的什么性质?演示等腰三角形的性质1: 等腰三角形的两个底角相等
(简写成“等边对等角”)注意:
在 三角形中,等边对等角。用符号语言表示为: 在△ABC中,
∵ AC=AB
∴ ∠B=∠C ( )等边对等角等腰三角形的性质2:等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 12D等腰三角形“三线合一”的性质用符号语言表示为:12B DCD12ADBCADBCB DCD⑵等腰三角形的顶角平分线、 底边上的中线、底边上的高互相重合, 简称等腰三角形三线合一。⑴等腰三角形的两个底角相等,
也就是说,在同一个三角形
中,等边对等角。等腰三角形的性质一分钟体会背会练习:已知:在△ABC中,AB = AC,
∠A = 50°, 求∠B 和 ∠C的度数。BA⒈等腰三角形一个底角为70°,它的顶角为______.⒉等腰三角形一个角为70°,它的另外两个角为
__________________.⒊等腰三角形一个角为110°,它的另外两个角为___________.40 °35 °,35 °70°,40° 或 55°,55° 巩固练习课本50页例14、已知等腰三角形一边的长为3,另一边的长为5,
求它的周长。解:分两种情况:
(1)当腰长为3时,有3+3>5符合要求,
∴此时三角形的周长为3×2+5=11;
(2)当腰长为5时,有5+5>3符合要求,
∴此时三角形的周长为5×2+3=13.跟踪练习:
等腰三角形的两边长分别为2和7,那么它
的周长是多少?思考:不等边三角形高、中线、角平分线的总条数为多少?等腰三角形(但不等边)高、中线、角平分线的总条数为多少?通过这堂课的学习,你得到了些什么?小结:等腰三角形⑵等腰三角形的顶角平分线、
底边上的中线和高互相重合,
简称等腰三角形三线合一。⑴等腰三角形的两个底角相等,
也就是说,在同一个三角形
中,等边对等角。再见!
底边底角底角顶角等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两边相等的三角形叫等腰三角形!
等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴.请大家观察试验,能发现等腰三角形的什么性质?演示等腰三角形的性质1: 等腰三角形的两个底角相等
(简写成“等边对等角”)注意:
在 三角形中,等边对等角。用符号语言表示为: 在△ABC中,
∵ AC=AB
∴ ∠B=∠C ( )等边对等角等腰三角形的性质2:等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。 12D等腰三角形“三线合一”的性质用符号语言表示为:12B DCD12ADBCADBCB DCD⑵等腰三角形的顶角平分线、 底边上的中线、底边上的高互相重合, 简称等腰三角形三线合一。⑴等腰三角形的两个底角相等,
也就是说,在同一个三角形
中,等边对等角。等腰三角形的性质一分钟体会背会练习:已知:在△ABC中,AB = AC,
∠A = 50°, 求∠B 和 ∠C的度数。BA⒈等腰三角形一个底角为70°,它的顶角为______.⒉等腰三角形一个角为70°,它的另外两个角为
__________________.⒊等腰三角形一个角为110°,它的另外两个角为___________.40 °35 °,35 °70°,40° 或 55°,55° 巩固练习课本50页例14、已知等腰三角形一边的长为3,另一边的长为5,
求它的周长。解:分两种情况:
(1)当腰长为3时,有3+3>5符合要求,
∴此时三角形的周长为3×2+5=11;
(2)当腰长为5时,有5+5>3符合要求,
∴此时三角形的周长为5×2+3=13.跟踪练习:
等腰三角形的两边长分别为2和7,那么它
的周长是多少?思考:不等边三角形高、中线、角平分线的总条数为多少?等腰三角形(但不等边)高、中线、角平分线的总条数为多少?通过这堂课的学习,你得到了些什么?小结:等腰三角形⑵等腰三角形的顶角平分线、
底边上的中线和高互相重合,
简称等腰三角形三线合一。⑴等腰三角形的两个底角相等,
也就是说,在同一个三角形
中,等边对等角。再见!
