等腰三角形的判定
图片预览




文档简介
(共19张PPT)
上节课我们学习了等腰三角形的哪些性质?
1、等腰三角形的两个底角相等.也就是说,在同一个三角形中,等边对等角;
2、等腰三角形的顶角平分线、底边上的中线和高互相重合, 简称等腰三角形三线合一.
等腰三角形的判定
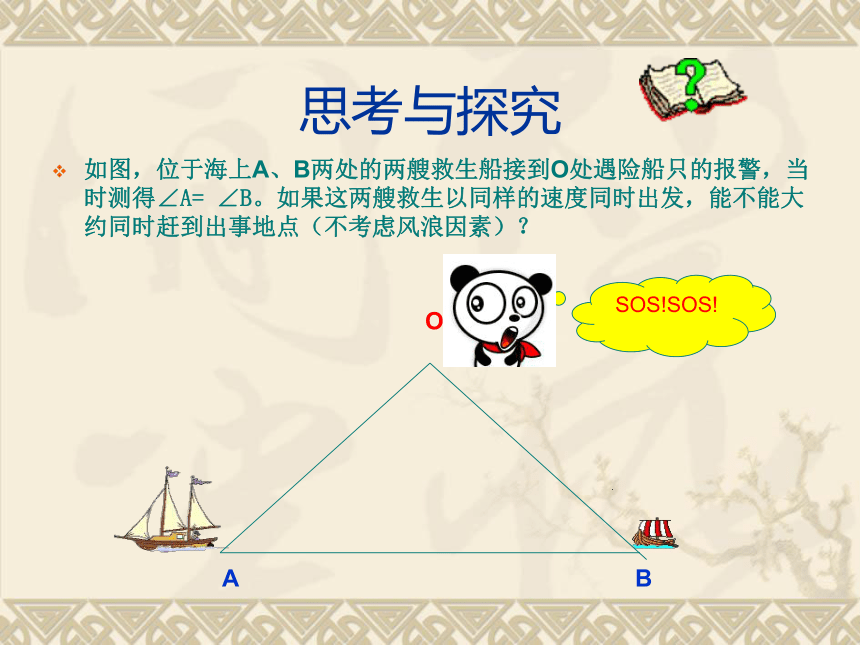
思考与探究
如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A= ∠B。如果这两艘救生以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
A
B
O
SOS!SOS!
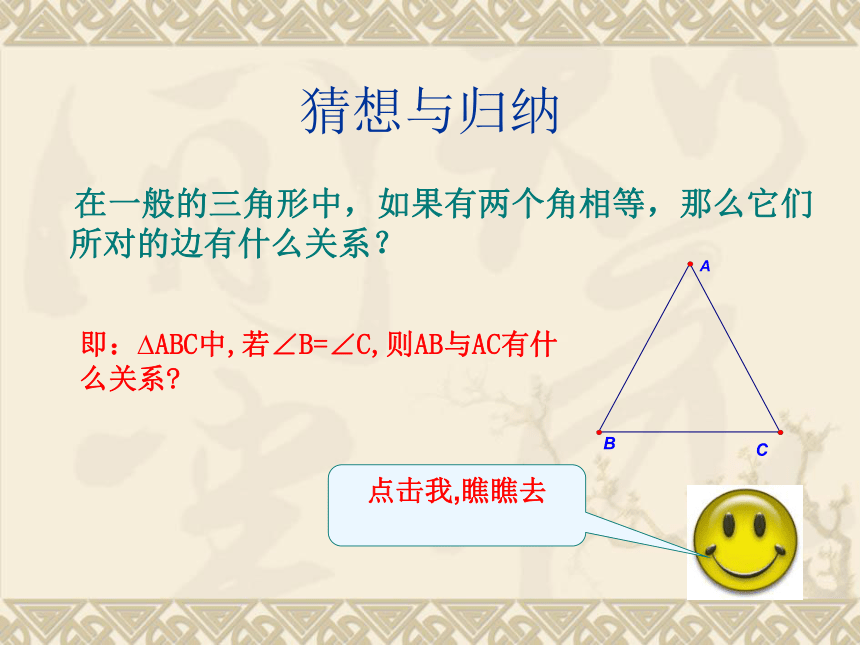
猜想与归纳
在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
即: ABC中,若∠B=∠C,则AB与AC有什么关系
点击我,瞧瞧去
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)
ABC中,
∵∠B=∠C
∴AB=AC
几何语言表示如下:
等腰三角形的判定方法
A
B
O
SOS!SOS!
总结 :现在你有哪些方法可以判定等腰三角形
(1)有两边相等的三角形是等腰三角形;
(2)如果一个三角形中有两个角相等,那么它是等腰三角形.
例题分析
例1、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
已知:∠CAE是 ABC的外角,∠1=∠2,AD//BC,(如图),求证:AB=AC。
证明:
∵AD//BC
∴∠1=∠B
∴∠2=∠C
又已知∠1=∠2
∴∠B=∠C
AB=AC
(_______________________)
(_____________________________)
(____________________)
两直线平行,内错角相等
等角对等边
两直线平行,同位角相等
1、如图,已知∠A=36°,∠DBC=36°,∠C=72°,
图中有多少个等腰三角形。
△ABC
△ABD
△BCD
挑战自我
2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?
A
B
C
E
D
C
答:
重合部分是一个等腰三角形。
∵由折叠可知∠CED=∠AEB,∠C=∠A ,CD=AB,
∴ EAB≌ ECD(AAS)
∴EB=ED
3、如图,BD是等腰三角形ABC的底边AC上的高,DE∥BC,交AB于点E. 判断△BDE是不是等腰三角形,并说明理由.
A
E
D
C
B
4、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。
证明:
∵ OA=OB
∴∠OAB=∠0BA
又∵ AB∥DC
∴∠OCD=∠OAB
∠0DC =∠0BA(平行线的性质)
∴∠OCD=∠ODC
∴OC=OD
5、如图, ABC中,BC=BA,∠A=600,BD是AC边的中线,延长BC到E,使CE=CD,求证:DE=DB
提示:
∵ BA=BC
∴∠BCA=∠A=600(等边对等角)
∵ CE=CD
∴∠E=∠CDE=300(三角形外角性质)
∵ BD是AC边的中线
∴∠DBC=300
∴DE=DB(等角对等边)
若DB是AC边上的高,上述结论还成立吗?
若DB是AC边上的高,上述结论仍成立
6、如图, ABC中,∠ABC、∠ACB的平分线交于点O,过点O作DE//BC,分别交AB、AC于点D、E,求证:BD+EC=DE
提示:
∵ DE//BC
∴∠OBC=∠DOB,∠OCB=∠EOC
∵ BO、CO分别平分∠ABC、∠ACB
∴∠DBO=∠DOB=∠OBC,∠ECO=∠EOC=∠OCB
∴BD=DO,CE=OE
∴BD+EC=DO+OE=DE
(等角对等边)
生活应用
上午8时,一条船从海岛A出发,以15海里的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得∠NAC=420,∠NBC=840,求从海岛B到灯塔C的距离。
A
B
C
N
解:
∵ ∠NBC=∠A+∠C
(三角形的一个外角等于不相邻的两个内角的和)
∴∠C= 840-420=420
∴BA=BC(等角对等边)
∵ AB=15(10-8)=30
∴BC=BA=30(海里)
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
小 结
著名的数学家,莫斯科大学教授雅洁卡提出:“解题就是把要解的题转化为已经解过的题”。许多题目我们都解过,怎样转化呢?加油吧!
上节课我们学习了等腰三角形的哪些性质?
1、等腰三角形的两个底角相等.也就是说,在同一个三角形中,等边对等角;
2、等腰三角形的顶角平分线、底边上的中线和高互相重合, 简称等腰三角形三线合一.
等腰三角形的判定
思考与探究
如图,位于海上A、B两处的两艘救生船接到O处遇险船只的报警,当时测得∠A= ∠B。如果这两艘救生以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
A
B
O
SOS!SOS!
猜想与归纳
在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?
即: ABC中,若∠B=∠C,则AB与AC有什么关系
点击我,瞧瞧去
如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”)
ABC中,
∵∠B=∠C
∴AB=AC
几何语言表示如下:
等腰三角形的判定方法
A
B
O
SOS!SOS!
总结 :现在你有哪些方法可以判定等腰三角形
(1)有两边相等的三角形是等腰三角形;
(2)如果一个三角形中有两个角相等,那么它是等腰三角形.
例题分析
例1、求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。
已知:∠CAE是 ABC的外角,∠1=∠2,AD//BC,(如图),求证:AB=AC。
证明:
∵AD//BC
∴∠1=∠B
∴∠2=∠C
又已知∠1=∠2
∴∠B=∠C
AB=AC
(_______________________)
(_____________________________)
(____________________)
两直线平行,内错角相等
等角对等边
两直线平行,同位角相等
1、如图,已知∠A=36°,∠DBC=36°,∠C=72°,
图中有多少个等腰三角形。
△ABC
△ABD
△BCD
挑战自我
2、如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?
A
B
C
E
D
C
答:
重合部分是一个等腰三角形。
∵由折叠可知∠CED=∠AEB,∠C=∠A ,CD=AB,
∴ EAB≌ ECD(AAS)
∴EB=ED
3、如图,BD是等腰三角形ABC的底边AC上的高,DE∥BC,交AB于点E. 判断△BDE是不是等腰三角形,并说明理由.
A
E
D
C
B
4、如图,AC和BD相交于点O,且AB∥DC,OA=OB,求证:OC=OD。
证明:
∵ OA=OB
∴∠OAB=∠0BA
又∵ AB∥DC
∴∠OCD=∠OAB
∠0DC =∠0BA(平行线的性质)
∴∠OCD=∠ODC
∴OC=OD
5、如图, ABC中,BC=BA,∠A=600,BD是AC边的中线,延长BC到E,使CE=CD,求证:DE=DB
提示:
∵ BA=BC
∴∠BCA=∠A=600(等边对等角)
∵ CE=CD
∴∠E=∠CDE=300(三角形外角性质)
∵ BD是AC边的中线
∴∠DBC=300
∴DE=DB(等角对等边)
若DB是AC边上的高,上述结论还成立吗?
若DB是AC边上的高,上述结论仍成立
6、如图, ABC中,∠ABC、∠ACB的平分线交于点O,过点O作DE//BC,分别交AB、AC于点D、E,求证:BD+EC=DE
提示:
∵ DE//BC
∴∠OBC=∠DOB,∠OCB=∠EOC
∵ BO、CO分别平分∠ABC、∠ACB
∴∠DBO=∠DOB=∠OBC,∠ECO=∠EOC=∠OCB
∴BD=DO,CE=OE
∴BD+EC=DO+OE=DE
(等角对等边)
生活应用
上午8时,一条船从海岛A出发,以15海里的速度向正北航行,10时到达海岛B处,从A、B望灯塔C,测得∠NAC=420,∠NBC=840,求从海岛B到灯塔C的距离。
A
B
C
N
解:
∵ ∠NBC=∠A+∠C
(三角形的一个外角等于不相邻的两个内角的和)
∴∠C= 840-420=420
∴BA=BC(等角对等边)
∵ AB=15(10-8)=30
∴BC=BA=30(海里)
名称 图 形 概 念 性质与边角关系 判 定
等
腰
三
角
形
A
B
C
有两边相等的三角形是等腰三角形
2.等边对等角
3. 三线合一
4.是轴对称图形
2.等角对等边
1.两边相等
1.两腰相等
小 结
著名的数学家,莫斯科大学教授雅洁卡提出:“解题就是把要解的题转化为已经解过的题”。许多题目我们都解过,怎样转化呢?加油吧!
