有理数乘方(浙江省金华市金华县)
文档属性
| 名称 | 有理数乘方(浙江省金华市金华县) |  | |
| 格式 | rar | ||
| 文件大小 | 581.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-06 11:18:00 | ||
图片预览



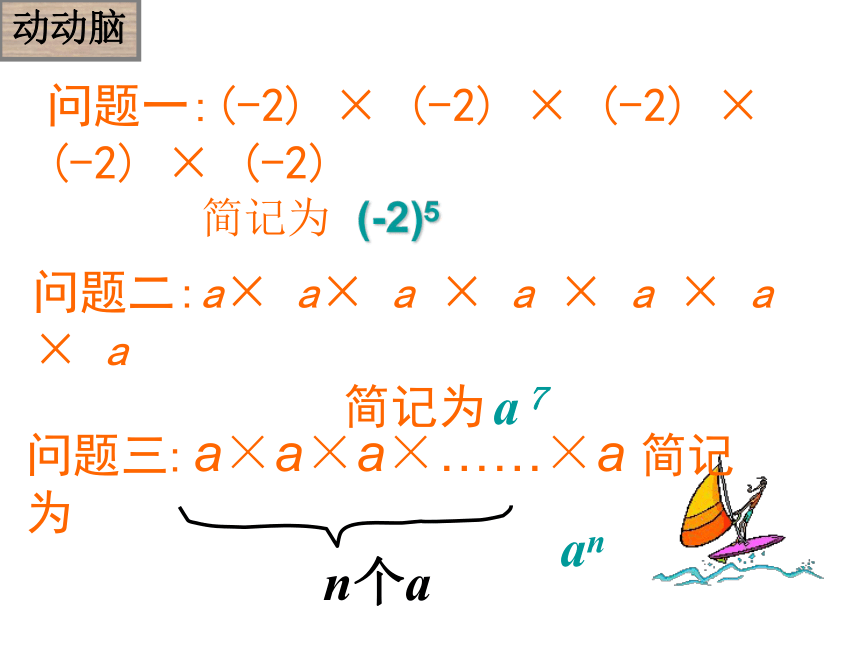




文档简介
课件36张PPT。
1.掌握乘方的意义,乘方的运算与乘法运算的关系.
2.掌握底数,指数和幂的概念,会求有理数的正整数指数幂(即会求有理数的乘方运算)
学习目标: 问题1:简化相同加数的加法.
6+6+6+6=
10+10+10+10+10+10=
2+2+2+2+2+2+2+2+2+2=
6×410×6
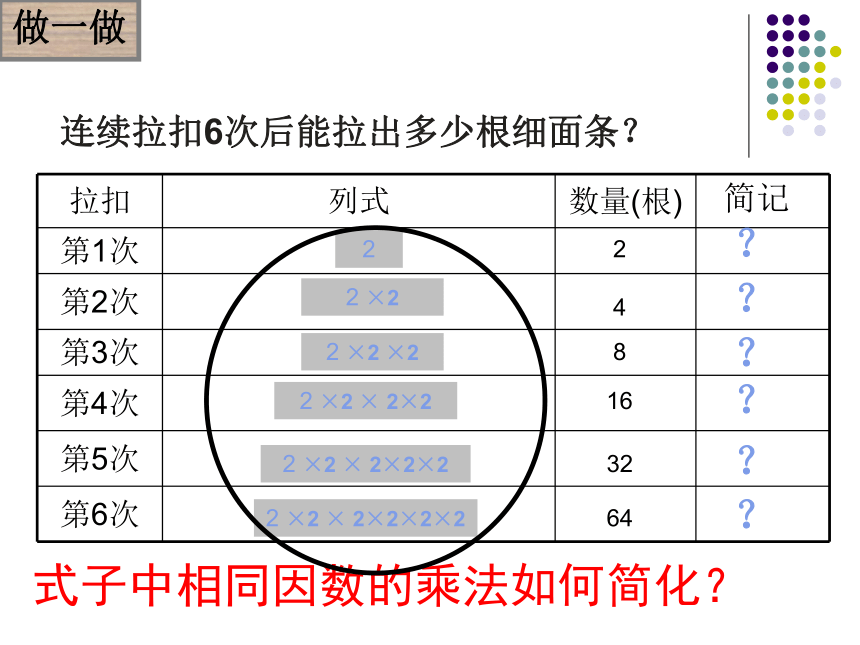
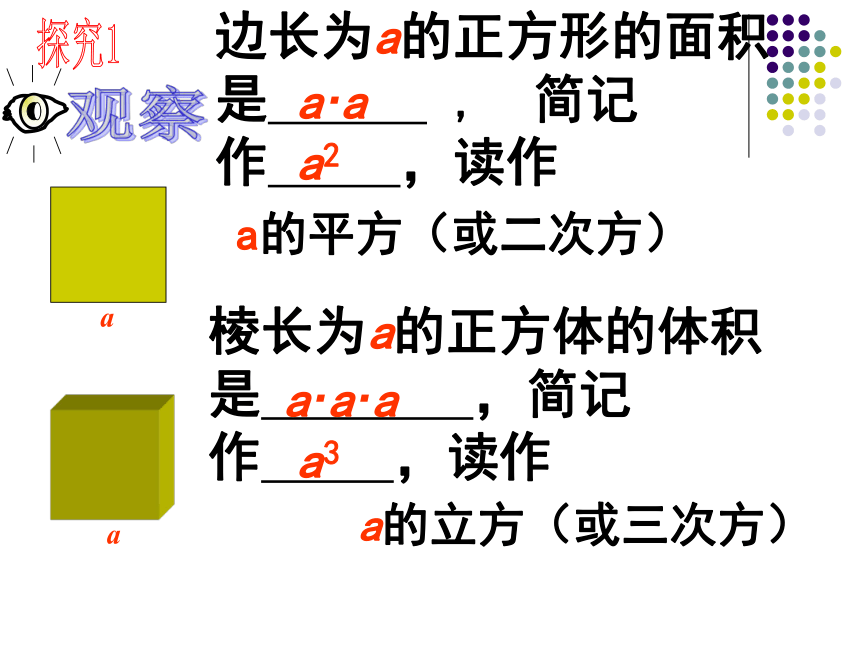
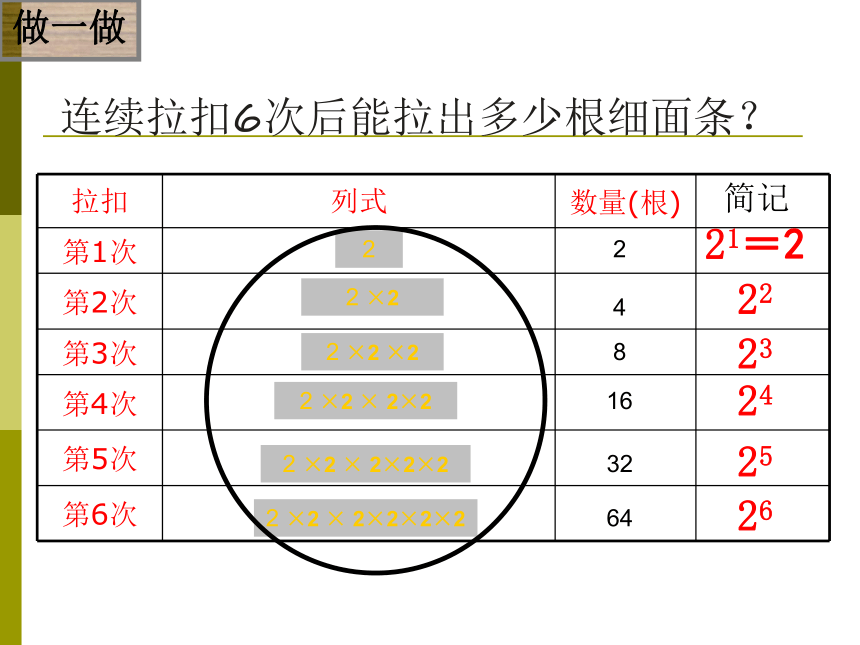
2×10 手工拉面是我国的传统面食,制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,每次对折称为一扣。问题2连续拉扣6次后能拉出多少根细面条?简记22 ×22 ×2 ×22 ×2 × 2×2????248162 ×2 × 2×2×2322 ×2 × 2×2×2×264??式子中相同因数的乘法如何简化?做一做1.5.1 乘方a边长为a的正方形的面积是 , 简记作 ,读作 棱长为a的正方体的体积是 ,简记作 ,读作 a探究1a·aa2a的平方(或二次方)a·a·aa3a的立方(或三次方)问题一:(-2) × (-2) × (-2) × (-2) × (-2) 简记为 动动脑(-2)5问题二:a× a× a × a × a × a × a 简记为 问题三: a×a×a×……×a 简记为 n个aa7an一般地,几个相同的因数a 相乘,即
记作: 。 读作:a的n次方求n个相同因数的积的 ,叫做
乘方的结果叫做幂。运算乘方。结果幂也可读作a的n次幂概 念乘方。运算指数底数幂 如:在 中,底数是( )
指数是( )
读作( )
949的4次方
或9的4次幂呢?连续拉扣6次后能拉出多少根细面条?简记22 ×22 ×2 ×22 ×2 × 2×222232421=2248162 ×2 × 2×2×2322 ×2 × 2×2×2×2642526做一做指出下列每个的底数和指数,分别表示的意义是什么?试试你的火眼金睛,6 请指出下列各组数的意义,结果
一样吗?当乘方的底数是负数或分数时,要加括号。注意: 练习一
一、根据乘方的意义,把下列
乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3) = ;
4、 =
二、根据乘方的意义,把下列乘方写成乘法的形式:
1. =
2. =
3. =
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?22×22×2×21个30ˊ3个30ˊ2个30ˊ例1、根据乘方的意义计算
负数的奇次幂是___数
负数的偶次幂是___数。得出:正负9-321 本题4个幂,底数都是负数,为什么这4个幂两个是正数而另外两个是负数呢?你能发现其中的规律吗?想一想正数的奇次幂是什么数?0的任何正整数次幂都是0。正数的任何次幂都是正数;思考:0呢?正数的偶次幂是什么数?0的任何正整数次幂都是0。负数的奇次幂是负数;负数的偶次幂是正数;正数的任何次幂都是正数;归纳:(1) (2)
(3) (4)
(5) (6)
=1=1=-1=1=1=-12、-1的幂很有规律:
-1的奇次幂是-1 ,
-1的偶次幂是11、1的任何次幂都为1规律:若 为有理数,则 是什么数?思考:≥0非负性| |
例2、若 则a=_________;
若 ,则a=____,
b=___4,-4-12 练习二
1.平方等于它本身的数是_______,立方等于它本身的是______.
2.一个数的15次幂是负数,那么这个数的2003次幂是_____.
3.平方等于 的数是_____
立方等于 的数是_______.1641641 , 0±1,0负数5.a,b互为相反数(a≠b,b ≠ 0),n是自然数,则下面能成立的结论是( )
8.有一张厚度是0.1毫米的纸,将它对折1次后,可裁成2张,对折2次,3次可裁多少张?厚度为多少?折多少次可以超过自己的身高?这张纸折
30次后能超过珠穆朗玛峰吗?121123211234321本节课你学到了什么?1.有理数的乘方的意义和相关概念;2.乘方的有关性质;幂的底数是分数或负数时,底数
应该添上括号.课后拓展:乘方的故事 有一个长工到财主家去做工,他和财主商定:“第一天给一分钱,第二天给两分钱,以后每天是前一天的2倍.”财主答应了,到月底(30天)后,你猜一猜:财主会给长工多少工钱? 月底,长工兴冲冲的去领钱,他以为自己一下子可以领到一笔天文财富,结果财主只给了长工5分钱,而且还说是多给了他.你知道这是怎么回事吗? 长工算法:第一天1分,第二天2分,第三天4分,第四天16分,第五天256分…… 财主算法:第一天0.01元,第二天0.02元,第三天0.0004元,第四天0.00000016元……分 析试一试 再见
1.掌握乘方的意义,乘方的运算与乘法运算的关系.
2.掌握底数,指数和幂的概念,会求有理数的正整数指数幂(即会求有理数的乘方运算)
学习目标: 问题1:简化相同加数的加法.
6+6+6+6=
10+10+10+10+10+10=
2+2+2+2+2+2+2+2+2+2=
6×410×6
2×10 手工拉面是我国的传统面食,制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,每次对折称为一扣。问题2连续拉扣6次后能拉出多少根细面条?简记22 ×22 ×2 ×22 ×2 × 2×2????248162 ×2 × 2×2×2322 ×2 × 2×2×2×264??式子中相同因数的乘法如何简化?做一做1.5.1 乘方a边长为a的正方形的面积是 , 简记作 ,读作 棱长为a的正方体的体积是 ,简记作 ,读作 a探究1a·aa2a的平方(或二次方)a·a·aa3a的立方(或三次方)问题一:(-2) × (-2) × (-2) × (-2) × (-2) 简记为 动动脑(-2)5问题二:a× a× a × a × a × a × a 简记为 问题三: a×a×a×……×a 简记为 n个aa7an一般地,几个相同的因数a 相乘,即
记作: 。 读作:a的n次方求n个相同因数的积的 ,叫做
乘方的结果叫做幂。运算乘方。结果幂也可读作a的n次幂概 念乘方。运算指数底数幂 如:在 中,底数是( )
指数是( )
读作( )
949的4次方
或9的4次幂呢?连续拉扣6次后能拉出多少根细面条?简记22 ×22 ×2 ×22 ×2 × 2×222232421=2248162 ×2 × 2×2×2322 ×2 × 2×2×2×2642526做一做指出下列每个的底数和指数,分别表示的意义是什么?试试你的火眼金睛,6 请指出下列各组数的意义,结果
一样吗?当乘方的底数是负数或分数时,要加括号。注意: 练习一
一、根据乘方的意义,把下列
乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3) = ;
4、 =
二、根据乘方的意义,把下列乘方写成乘法的形式:
1. =
2. =
3. =
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?22×22×2×21个30ˊ3个30ˊ2个30ˊ例1、根据乘方的意义计算
负数的奇次幂是___数
负数的偶次幂是___数。得出:正负9-321 本题4个幂,底数都是负数,为什么这4个幂两个是正数而另外两个是负数呢?你能发现其中的规律吗?想一想正数的奇次幂是什么数?0的任何正整数次幂都是0。正数的任何次幂都是正数;思考:0呢?正数的偶次幂是什么数?0的任何正整数次幂都是0。负数的奇次幂是负数;负数的偶次幂是正数;正数的任何次幂都是正数;归纳:(1) (2)
(3) (4)
(5) (6)
=1=1=-1=1=1=-12、-1的幂很有规律:
-1的奇次幂是-1 ,
-1的偶次幂是11、1的任何次幂都为1规律:若 为有理数,则 是什么数?思考:≥0非负性| |
例2、若 则a=_________;
若 ,则a=____,
b=___4,-4-12 练习二
1.平方等于它本身的数是_______,立方等于它本身的是______.
2.一个数的15次幂是负数,那么这个数的2003次幂是_____.
3.平方等于 的数是_____
立方等于 的数是_______.1641641 , 0±1,0负数5.a,b互为相反数(a≠b,b ≠ 0),n是自然数,则下面能成立的结论是( )
8.有一张厚度是0.1毫米的纸,将它对折1次后,可裁成2张,对折2次,3次可裁多少张?厚度为多少?折多少次可以超过自己的身高?这张纸折
30次后能超过珠穆朗玛峰吗?121123211234321本节课你学到了什么?1.有理数的乘方的意义和相关概念;2.乘方的有关性质;幂的底数是分数或负数时,底数
应该添上括号.课后拓展:乘方的故事 有一个长工到财主家去做工,他和财主商定:“第一天给一分钱,第二天给两分钱,以后每天是前一天的2倍.”财主答应了,到月底(30天)后,你猜一猜:财主会给长工多少工钱? 月底,长工兴冲冲的去领钱,他以为自己一下子可以领到一笔天文财富,结果财主只给了长工5分钱,而且还说是多给了他.你知道这是怎么回事吗? 长工算法:第一天1分,第二天2分,第三天4分,第四天16分,第五天256分…… 财主算法:第一天0.01元,第二天0.02元,第三天0.0004元,第四天0.00000016元……分 析试一试 再见
