第二十四章圆(单元测试)(含答案)2023-2024学年人教版数学九年级上册
文档属性
| 名称 | 第二十四章圆(单元测试)(含答案)2023-2024学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 502.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 09:30:21 | ||
图片预览

文档简介
第二十四章圆(单元测试)
2023-2024学年九年级上册数学人教版
一、单选题(共10小题,满分40分)
1.如图,点A,B,C在⊙O上,∠AOB=70°,则∠ACB的度数是 ( )
A.70°
B.30°
C.35°
D.40°
2.如图所示,A、B、C、D是⊙O上的点,,下列结论错误的是( )
A. B. C. D.
3.如图3,四边形ABCD是⊙O的内接四边形,∠B=90 ,∠A=60 ,AB=3,CD=2,则AD的长为( )
A. B. C. D.3
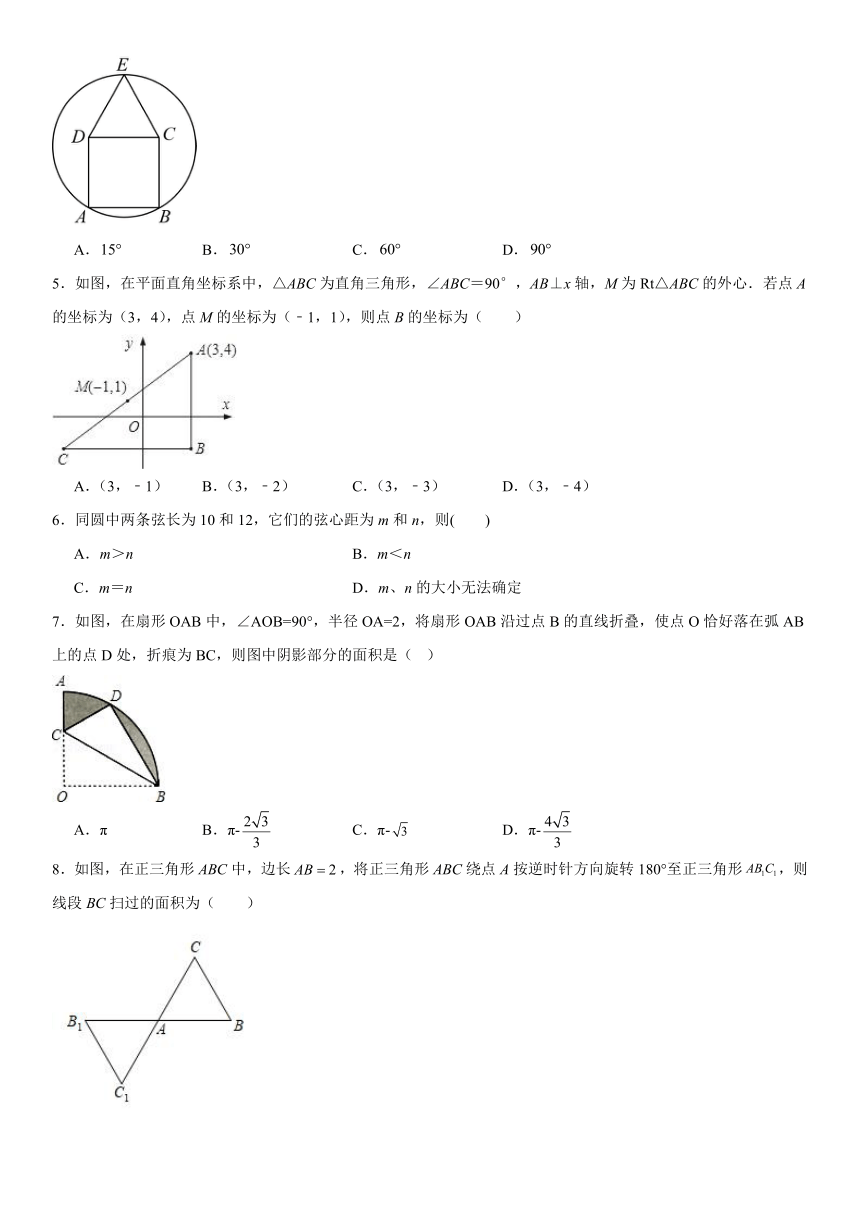
4.将边长相等的正方形和等边三角形如图放置,过、、三点作圆,则所对的圆心角的度数是( )
A. B. C. D.
5.如图,在平面直角坐标系中,△ABC为直角三角形,∠ABC=90°,AB⊥x轴,M为Rt△ABC的外心.若点A的坐标为(3,4),点M的坐标为(﹣1,1),则点B的坐标为( )
A.(3,﹣1) B.(3,﹣2) C.(3,﹣3) D.(3,﹣4)
6.同圆中两条弦长为10和12,它们的弦心距为m和n,则( )
A.m>n B.m<n
C.m=n D.m、n的大小无法确定
7.如图,在扇形OAB中,∠AOB=90°,半径OA=2,将扇形OAB沿过点B的直线折叠,使点O恰好落在弧AB上的点D处,折痕为BC,则图中阴影部分的面积是( )
A.π B.π- C.π- D.π-
8.如图,在正三角形ABC中,边长,将正三角形ABC绕点A按逆时针方向旋转180°至正三角形,则线段BC扫过的面积为( )
A. B. C. D.
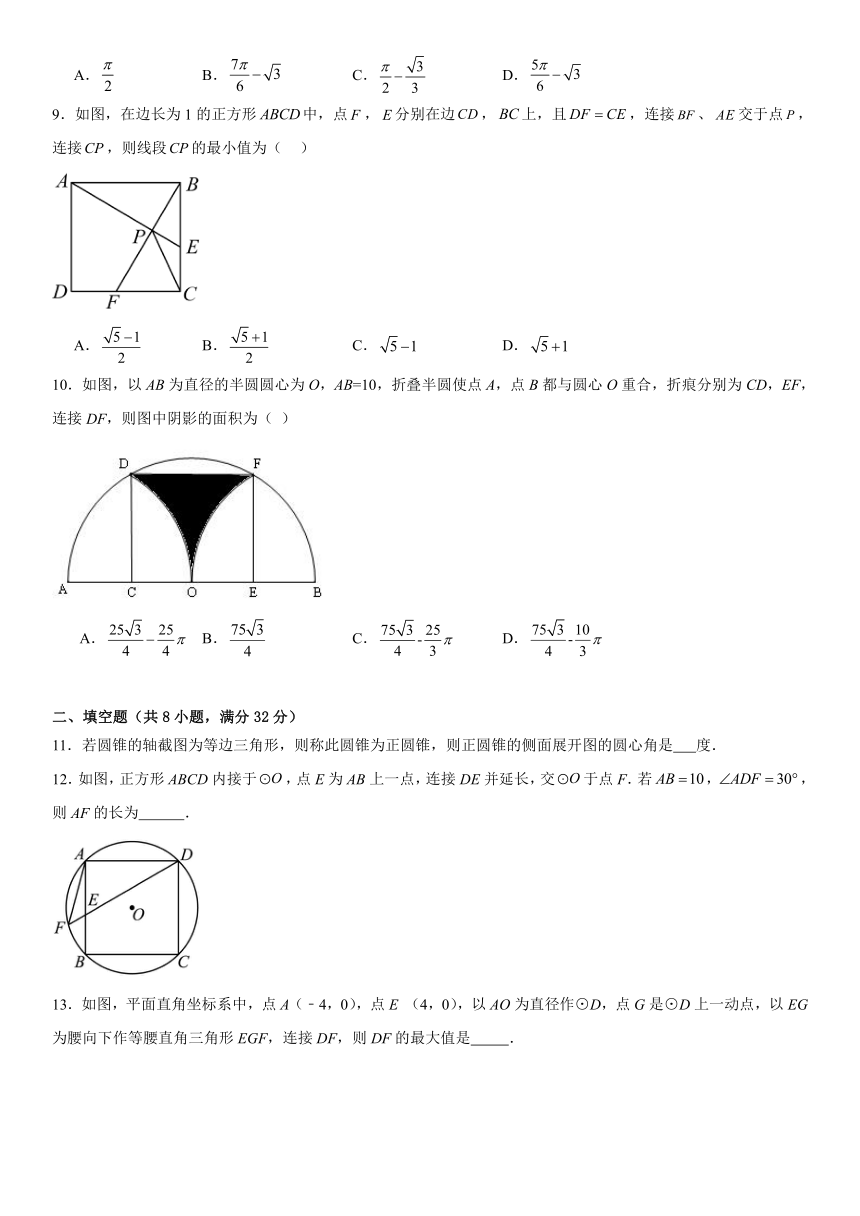
9.如图,在边长为1的正方形中,点,分别在边,上,且,连接、交于点,连接,则线段的最小值为( )
A. B. C. D.
10.如图,以AB为直径的半圆圆心为O,AB=10,折叠半圆使点A,点B都与圆心O重合,折痕分别为CD,EF,连接DF,则图中阴影的面积为( )
A. B. C. D.
二、填空题(共8小题,满分32分)
11.若圆锥的轴截图为等边三角形,则称此圆锥为正圆锥,则正圆锥的侧面展开图的圆心角是 度.
12.如图,正方形ABCD内接于,点E为AB上一点,连接DE并延长,交于点F.若,,则AF的长为 .
13.如图,平面直角坐标系中,点A(﹣4,0),点E (4,0),以AO为直径作⊙D,点G是⊙D上一动点,以EG为腰向下作等腰直角三角形EGF,连接DF,则DF的最大值是 .
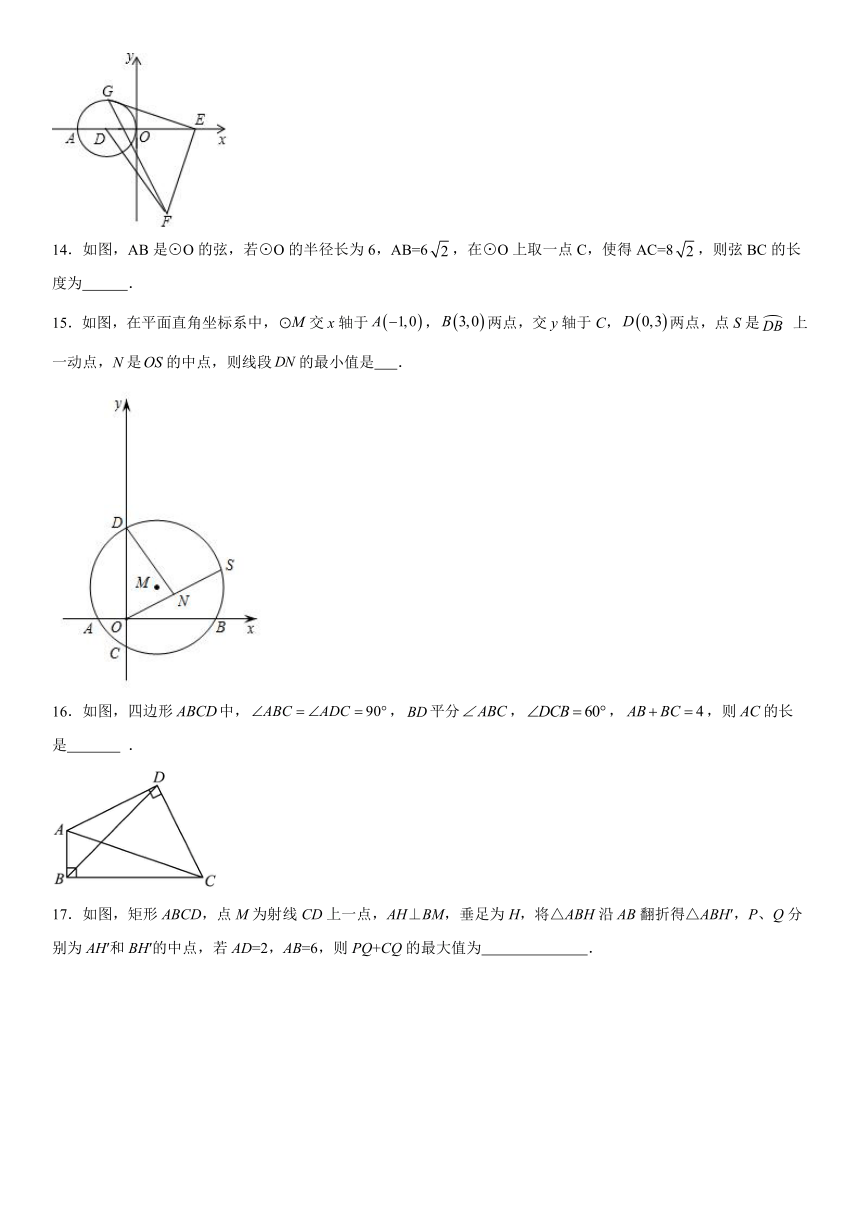
14.如图,AB是⊙O的弦,若⊙O的半径长为6,AB=6,在⊙O上取一点C,使得AC=8,则弦BC的长度为 .
15.如图,在平面直角坐标系中,交x轴于,两点,交y轴于C,两点,点S是 上一动点,N是的中点,则线段的最小值是 .
16.如图,四边形中,,平分,,,则的长是 .
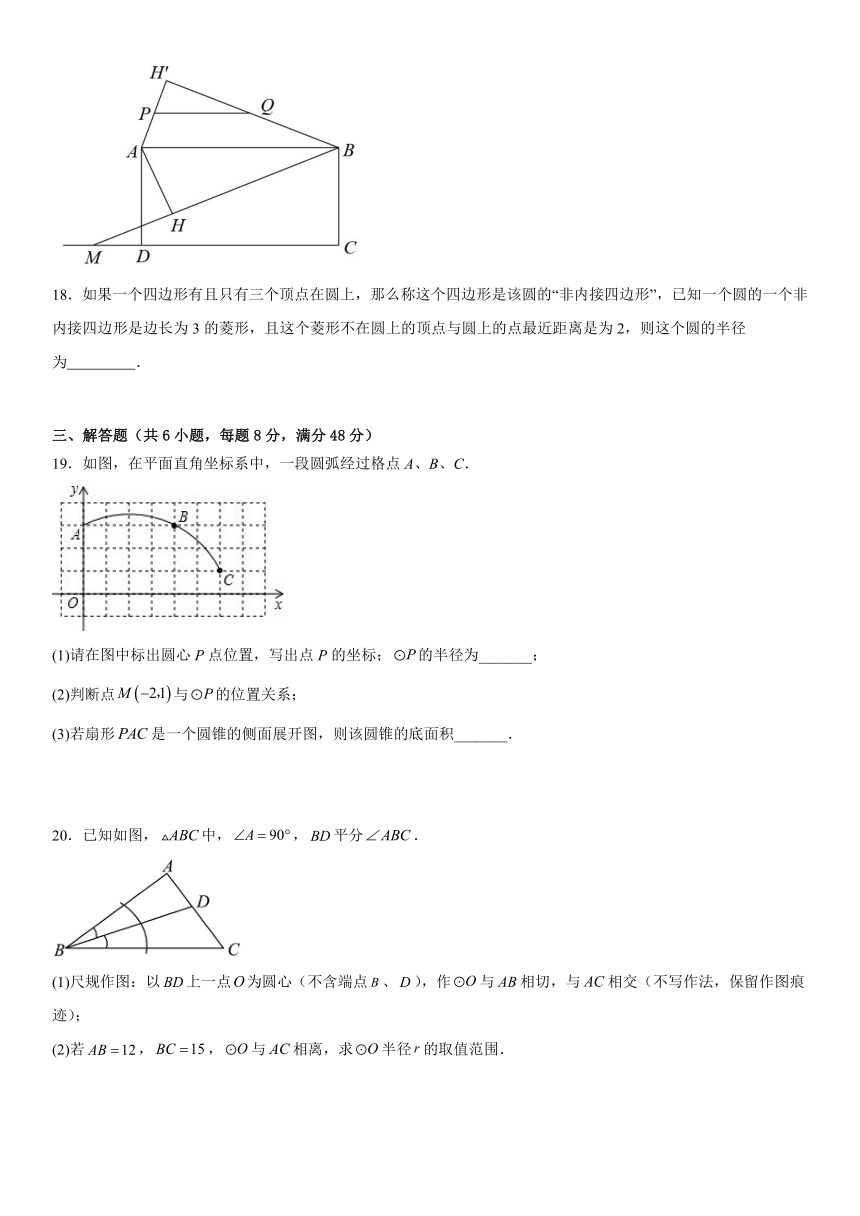
17.如图,矩形ABCD,点M为射线CD上一点,AH⊥BM,垂足为H,将△ABH沿AB翻折得△ABH′,P、Q分别为AH′和BH′的中点,若AD=2,AB=6,则PQ+CQ的最大值为 .
18.如果一个四边形有且只有三个顶点在圆上,那么称这个四边形是该圆的“非内接四边形”,已知一个圆的一个非内接四边形是边长为3的菱形,且这个菱形不在圆上的顶点与圆上的点最近距离是为2,则这个圆的半径为 .
三、解答题(共6小题,每题8分,满分48分)
19.如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.
(1)请在图中标出圆心P点位置,写出点P的坐标;的半径为_______;
(2)判断点与的位置关系;
(3)若扇形是一个圆锥的侧面展开图,则该圆锥的底面积_______.
20.已知如图,中,,平分.
(1)尺规作图:以上一点为圆心(不含端点、),作与相切,与相交(不写作法,保留作图痕迹);
(2)若,,与相离,求半径的取值范围.
21.如图,在中,,点在上,以为圆心,为半径的半圆分别交,于点,且点是弧的中点.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
22.如图,四边形内接于,,点D在上.
(1)如图①,若,求的大小;
(2)如图②,若为的直径,过点A作的切线,交的延长线于点E,求的大小.
23.在平面直角坐标系中,对于点,给出如下定义:当点,满足时,称点N是点M的负等积点已知点.
(1)在,,,中,点M的负等积点是______.
(2)如果点M的负等积点N在双曲线上,求点N的坐标;
(3)已知点,,的半径为1,连接MP,点A在线段MP上.如果在上存在点A的负等积点,直接写出a的取值范围.
24.在平面直角坐标系中,对于点(不与点重合)和线段,给出如下定义:连接,平移线段,使点与线段的中点重合,得到线段,则称点为线段的“中移点”.已知的半径为1.
(1)如图,点,点,
点为与轴正半轴的交点,,求的值;
点为上一点,若在直线上存在线段的“中移点”,求的取值范围;
(2)点是上一点,点在线段上,且.若是外一点,点为线段的“中移点”,连接.当点在上运动时,直接写出长的最大值与最小值的差(用含的式子表示).
参考答案:
1.C
2.C
3.C
4.C
5.B
6.A
7.D
8.B
9.A
10.C
11.180
12.
13.6+2
14.8±2
15.
16.
17.7
18.或或
19.(1),
(2)点M在上
(3)
20.(1)11
(2)
21.(1)证明略
(2)
22.(1)
(2)
23.(1),
(2)或
(3)
24.(1)①或;②
(2)
2023-2024学年九年级上册数学人教版
一、单选题(共10小题,满分40分)
1.如图,点A,B,C在⊙O上,∠AOB=70°,则∠ACB的度数是 ( )
A.70°
B.30°
C.35°
D.40°
2.如图所示,A、B、C、D是⊙O上的点,,下列结论错误的是( )
A. B. C. D.
3.如图3,四边形ABCD是⊙O的内接四边形,∠B=90 ,∠A=60 ,AB=3,CD=2,则AD的长为( )
A. B. C. D.3
4.将边长相等的正方形和等边三角形如图放置,过、、三点作圆,则所对的圆心角的度数是( )
A. B. C. D.
5.如图,在平面直角坐标系中,△ABC为直角三角形,∠ABC=90°,AB⊥x轴,M为Rt△ABC的外心.若点A的坐标为(3,4),点M的坐标为(﹣1,1),则点B的坐标为( )
A.(3,﹣1) B.(3,﹣2) C.(3,﹣3) D.(3,﹣4)
6.同圆中两条弦长为10和12,它们的弦心距为m和n,则( )
A.m>n B.m<n
C.m=n D.m、n的大小无法确定
7.如图,在扇形OAB中,∠AOB=90°,半径OA=2,将扇形OAB沿过点B的直线折叠,使点O恰好落在弧AB上的点D处,折痕为BC,则图中阴影部分的面积是( )
A.π B.π- C.π- D.π-
8.如图,在正三角形ABC中,边长,将正三角形ABC绕点A按逆时针方向旋转180°至正三角形,则线段BC扫过的面积为( )
A. B. C. D.
9.如图,在边长为1的正方形中,点,分别在边,上,且,连接、交于点,连接,则线段的最小值为( )
A. B. C. D.
10.如图,以AB为直径的半圆圆心为O,AB=10,折叠半圆使点A,点B都与圆心O重合,折痕分别为CD,EF,连接DF,则图中阴影的面积为( )
A. B. C. D.
二、填空题(共8小题,满分32分)
11.若圆锥的轴截图为等边三角形,则称此圆锥为正圆锥,则正圆锥的侧面展开图的圆心角是 度.
12.如图,正方形ABCD内接于,点E为AB上一点,连接DE并延长,交于点F.若,,则AF的长为 .
13.如图,平面直角坐标系中,点A(﹣4,0),点E (4,0),以AO为直径作⊙D,点G是⊙D上一动点,以EG为腰向下作等腰直角三角形EGF,连接DF,则DF的最大值是 .
14.如图,AB是⊙O的弦,若⊙O的半径长为6,AB=6,在⊙O上取一点C,使得AC=8,则弦BC的长度为 .
15.如图,在平面直角坐标系中,交x轴于,两点,交y轴于C,两点,点S是 上一动点,N是的中点,则线段的最小值是 .
16.如图,四边形中,,平分,,,则的长是 .
17.如图,矩形ABCD,点M为射线CD上一点,AH⊥BM,垂足为H,将△ABH沿AB翻折得△ABH′,P、Q分别为AH′和BH′的中点,若AD=2,AB=6,则PQ+CQ的最大值为 .
18.如果一个四边形有且只有三个顶点在圆上,那么称这个四边形是该圆的“非内接四边形”,已知一个圆的一个非内接四边形是边长为3的菱形,且这个菱形不在圆上的顶点与圆上的点最近距离是为2,则这个圆的半径为 .
三、解答题(共6小题,每题8分,满分48分)
19.如图,在平面直角坐标系中,一段圆弧经过格点A、B、C.
(1)请在图中标出圆心P点位置,写出点P的坐标;的半径为_______;
(2)判断点与的位置关系;
(3)若扇形是一个圆锥的侧面展开图,则该圆锥的底面积_______.
20.已知如图,中,,平分.
(1)尺规作图:以上一点为圆心(不含端点、),作与相切,与相交(不写作法,保留作图痕迹);
(2)若,,与相离,求半径的取值范围.
21.如图,在中,,点在上,以为圆心,为半径的半圆分别交,于点,且点是弧的中点.
(1)求证:是的切线;
(2)若,求图中阴影部分的面积(结果保留).
22.如图,四边形内接于,,点D在上.
(1)如图①,若,求的大小;
(2)如图②,若为的直径,过点A作的切线,交的延长线于点E,求的大小.
23.在平面直角坐标系中,对于点,给出如下定义:当点,满足时,称点N是点M的负等积点已知点.
(1)在,,,中,点M的负等积点是______.
(2)如果点M的负等积点N在双曲线上,求点N的坐标;
(3)已知点,,的半径为1,连接MP,点A在线段MP上.如果在上存在点A的负等积点,直接写出a的取值范围.
24.在平面直角坐标系中,对于点(不与点重合)和线段,给出如下定义:连接,平移线段,使点与线段的中点重合,得到线段,则称点为线段的“中移点”.已知的半径为1.
(1)如图,点,点,
点为与轴正半轴的交点,,求的值;
点为上一点,若在直线上存在线段的“中移点”,求的取值范围;
(2)点是上一点,点在线段上,且.若是外一点,点为线段的“中移点”,连接.当点在上运动时,直接写出长的最大值与最小值的差(用含的式子表示).
参考答案:
1.C
2.C
3.C
4.C
5.B
6.A
7.D
8.B
9.A
10.C
11.180
12.
13.6+2
14.8±2
15.
16.
17.7
18.或或
19.(1),
(2)点M在上
(3)
20.(1)11
(2)
21.(1)证明略
(2)
22.(1)
(2)
23.(1),
(2)或
(3)
24.(1)①或;②
(2)
同课章节目录
