第2章 轴对称图形 复习练习 2023—2024学年苏科版数学八年级上册(含答案)
文档属性
| 名称 | 第2章 轴对称图形 复习练习 2023—2024学年苏科版数学八年级上册(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 796.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:00:00 | ||
图片预览

文档简介
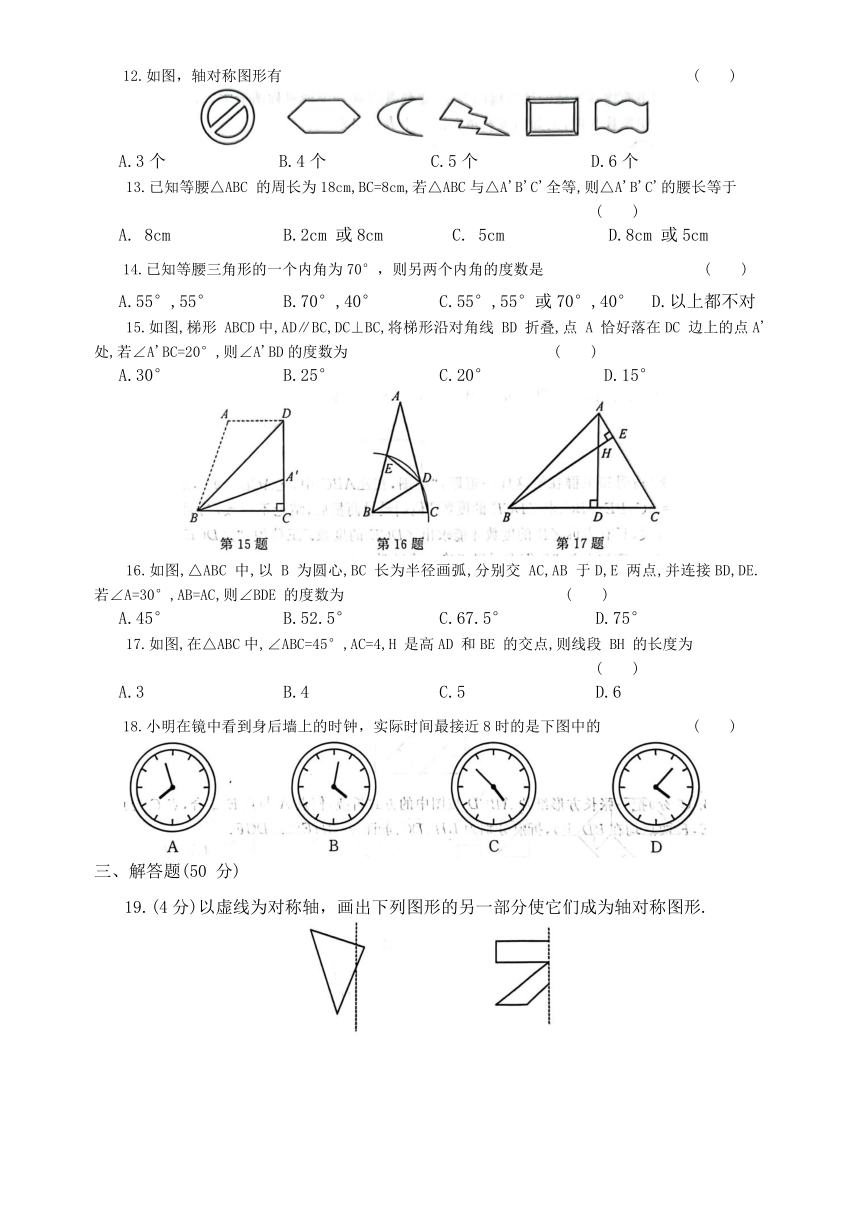
分类复习《轴对称图形》
测试时间:120 分钟 总分:100分
题号 一 二 三 总分
19 20 21 22 23 24 25 26
得分
一、填空题(每空2分,共26分)
1. M,N,A,B是同 平面上的四个点,如果 MA=MB,NA=NB,则点 . 在线段 的垂直平分线上.
2.角是轴对称图形,对称轴是 .
3.如图,已知CD 是AB 的垂直平分线,AC=3.9cm,BD=2.1cm,则四边形CBDA的周长为 .
4.等腰直角三角形的两锐角平分线相交所成的钝角的度数是 .
5.等腰三角形的 内角等于50°,则其他两个内角各为 .
6.如图,点P 为∠AOB 内一点,分别作出 P 点关于OA、OB的对称点P ,P ,连接P P 交 OA 于 M,交 OB 于 N, ,则△PMN的周长为 .
7.已知A( 1, 2)和B(1,3),将点 A 向 平移 个单位长度后得到的点与点 B 关于 y 轴对称.
8.如图,在△ABC中,AC=12cm,BC=8cm,AB的垂直平分线交AB 于点D,交AC于点E,则△BCE的周长为 cm.
9.如图,在等边△ABC中,BD=CE,AD 与BE 相交于点 F,则∠AFE= .
10.等边三角形的周长是 30cm,则其面积为 .
二、选择题(每题3 分,共 24分)
11.下列四个汽车标志图案中,不是轴对称图形的是 ( )
12.如图,轴对称图形有 ( )
A.3个 B.4个 C.5个 D.6个
13.已知等腰△ABC 的周长为18cm,BC=8cm,若△ABC与△A'B'C'全等,则△A'B'C'的腰长等于 ( )
A. 8cm B.2cm 或8cm C. 5cm D.8cm 或5cm
14.已知等腰三角形的一个内角为70°,则另两个内角的度数是 ( )
A.55°,55° B.70°,40° C.55°,55°或70°,40° D.以上都不对
15.如图,梯形 ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线 BD 折叠,点 A 恰好落在DC 边上的点A'处,若∠A'BC=20°,则∠A'BD的度数为 ( )
A.30° B.25° C.20° D.15°
16.如图,△ABC 中,以 B 为圆心,BC 长为半径画弧,分别交 AC,AB 于D,E 两点,并连接BD,DE.若∠A=30°,AB=AC,则∠BDE 的度数为 ( )
A.45° B.52.5° C.67.5° D.75°
17.如图,在△ABC中,∠ABC=45°,AC=4,H 是高AD 和BE 的交点,则线段 BH 的长度为 ( )
A.3 B.4 C.5 D.6
18.小明在镜中看到身后墙上的时钟,实际时间最接近8时的是下图中的 ( )
三、解答题(50 分)
19.(4分)以虚线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.
20.(6分)小明发现:若将 4 棵树栽于正方形的四个顶点上,如图①所示,则恰好构成一个轴对称图形.你还能找到其他两种栽树的方法,也使其组成一个轴对称图形吗 请分别在图②、③中表示出来.如果栽5棵,又如何呢 请在图④中表示出来.
21.(6分)一个等腰三角形的一个内角比另一个内角的2 倍少10°,求这个三角形的三个内角的度数.(考虑两种情况)
22.(4分)马明和王群在解这样一道题:“如图,在△ABC 中,∠ACB=90°,点 D、E 在边AB上,AD=AC,BE=BC.求∠DCE 的度数.”他们经过商量后,结论不一致,马明说:“∠DCE的值与∠B 有关,只有告诉∠B的度数才能求出∠DCE 的度数.”王群说:“∠DCE 的度数是一个定值,与∠B 的度数无关.”他们谁说得正确 请说明理由.
23.(6分)把一张长方形纸片 ABCD按图中的方式折叠,使点 A 与点 E 重合,点C 与点F重合(E,F 两点均在 BD 上),折痕分别为 BH,DG.求证:△BHE≌△DGF.
- 1
24.(8分)在△ABC中,∠BAC=90°,AC=8cm,AB(1)若△ABD 周长为 14 cm,求 AB 的长;
(2)求△ABC 的面积.
25.(8分)如图,OE,OF 所在直线分别是△ABC 中AB,AC 边的中垂线(即垂直平分线),∠OBC,∠OCB的平分线相交于点I,试判定 OI 与BC 的位置关系,并给出证明.
26.(8分)如图,延长△ABC 的各边,使得BF=AC,AE=CD=AB.顺次连接点 D,E,F,得到的△DEF 为等边三角形.
(1)试说明△AEF≌△CDE.
(2)△ABC 是等边三角形吗 为什么
分类复习《轴对称图形》
一、1. M N AB 2.角平分线所在的直线 3.12cm 4.135° 5.50°,80°或 65°,65° 6.15 7.上 58.20 9.60° 10.25 cm
二、 11. C 12. B 13. D 14. C 15. B 16. C 17. B 18. B
三、19.略
20.
21.40°,70°,70°或 85°,47.5°,47.5°
22.王群正确,理由:∵AD=AC,∴∠ACD=∠ADC.又∵∠ACD=∠DCE+∠ACE,∠ADC=∠BCD+∠B,∴∠ACE+∠DCE=∠BCD+∠B. ① ∵BE=BC,∴∠CED=∠ECB.∵∠CED=∠ACE+∠H,∠ECB=∠BCD+∠DCE,∴∠BCD+∠DCE=∠ACE+∠A. ② ①式+②式,得2∠DCE=∠A+∠B.∵∠ACB=90°,∴∠A+∠B=90°,∴2∠DCE=90°,∠DCE=45°.
23.证明:由折叠可知 ∠GFD=∠C=90°,AB=BE,CD=FD.∵ABCD 是长方形,∴AB∥CD,AB=CD.∵AB∥CD,∴∠ABD=∠CDB.∴∠EBH=∠GDF.∵AB=CD,∴BE=DF.在△BHE 和△DGF 中, .△BHE≌△DGF(ASA).
24.(1)6cm (2)24 cm
25. OI⊥BC.证明:连接AO,延长 OI 交 BC 于点M.∵OE,OF 所在直线分别为AB,AC 的中垂线,∴OA=OB,OA=OC,∴OB=OC.又∵BI,CI 分别为∠OBC,∠OCB 的平分线,∴点 I 必在∠BOC 的平分线上,∴∠BOI=∠COI.在△BOM 和△COM 中, ∠CMO.又∵∠BMO+∠CMO=180°,∴∠BMO=∠CMO=90°,∴OI⊥BC.
26.(1)∵BF=AC,AB=AE,∴FA=EC.∵△DEF 为等边三角形,∴EF=DE.又∵AE=CD,∴△AEF≌△CDE.
(2)是等边三角形,理由:由(1)知,△AEF≌△CDE,∴∠FEA=∠EDC,∵△DEF 是等边三角形,∴∠DEF=60°.∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF,∴∠BCA=60°.同理,∠BAC=60°.∴△ABC 是等边三角形.
测试时间:120 分钟 总分:100分
题号 一 二 三 总分
19 20 21 22 23 24 25 26
得分
一、填空题(每空2分,共26分)
1. M,N,A,B是同 平面上的四个点,如果 MA=MB,NA=NB,则点 . 在线段 的垂直平分线上.
2.角是轴对称图形,对称轴是 .
3.如图,已知CD 是AB 的垂直平分线,AC=3.9cm,BD=2.1cm,则四边形CBDA的周长为 .
4.等腰直角三角形的两锐角平分线相交所成的钝角的度数是 .
5.等腰三角形的 内角等于50°,则其他两个内角各为 .
6.如图,点P 为∠AOB 内一点,分别作出 P 点关于OA、OB的对称点P ,P ,连接P P 交 OA 于 M,交 OB 于 N, ,则△PMN的周长为 .
7.已知A( 1, 2)和B(1,3),将点 A 向 平移 个单位长度后得到的点与点 B 关于 y 轴对称.
8.如图,在△ABC中,AC=12cm,BC=8cm,AB的垂直平分线交AB 于点D,交AC于点E,则△BCE的周长为 cm.
9.如图,在等边△ABC中,BD=CE,AD 与BE 相交于点 F,则∠AFE= .
10.等边三角形的周长是 30cm,则其面积为 .
二、选择题(每题3 分,共 24分)
11.下列四个汽车标志图案中,不是轴对称图形的是 ( )
12.如图,轴对称图形有 ( )
A.3个 B.4个 C.5个 D.6个
13.已知等腰△ABC 的周长为18cm,BC=8cm,若△ABC与△A'B'C'全等,则△A'B'C'的腰长等于 ( )
A. 8cm B.2cm 或8cm C. 5cm D.8cm 或5cm
14.已知等腰三角形的一个内角为70°,则另两个内角的度数是 ( )
A.55°,55° B.70°,40° C.55°,55°或70°,40° D.以上都不对
15.如图,梯形 ABCD中,AD∥BC,DC⊥BC,将梯形沿对角线 BD 折叠,点 A 恰好落在DC 边上的点A'处,若∠A'BC=20°,则∠A'BD的度数为 ( )
A.30° B.25° C.20° D.15°
16.如图,△ABC 中,以 B 为圆心,BC 长为半径画弧,分别交 AC,AB 于D,E 两点,并连接BD,DE.若∠A=30°,AB=AC,则∠BDE 的度数为 ( )
A.45° B.52.5° C.67.5° D.75°
17.如图,在△ABC中,∠ABC=45°,AC=4,H 是高AD 和BE 的交点,则线段 BH 的长度为 ( )
A.3 B.4 C.5 D.6
18.小明在镜中看到身后墙上的时钟,实际时间最接近8时的是下图中的 ( )
三、解答题(50 分)
19.(4分)以虚线为对称轴,画出下列图形的另一部分使它们成为轴对称图形.
20.(6分)小明发现:若将 4 棵树栽于正方形的四个顶点上,如图①所示,则恰好构成一个轴对称图形.你还能找到其他两种栽树的方法,也使其组成一个轴对称图形吗 请分别在图②、③中表示出来.如果栽5棵,又如何呢 请在图④中表示出来.
21.(6分)一个等腰三角形的一个内角比另一个内角的2 倍少10°,求这个三角形的三个内角的度数.(考虑两种情况)
22.(4分)马明和王群在解这样一道题:“如图,在△ABC 中,∠ACB=90°,点 D、E 在边AB上,AD=AC,BE=BC.求∠DCE 的度数.”他们经过商量后,结论不一致,马明说:“∠DCE的值与∠B 有关,只有告诉∠B的度数才能求出∠DCE 的度数.”王群说:“∠DCE 的度数是一个定值,与∠B 的度数无关.”他们谁说得正确 请说明理由.
23.(6分)把一张长方形纸片 ABCD按图中的方式折叠,使点 A 与点 E 重合,点C 与点F重合(E,F 两点均在 BD 上),折痕分别为 BH,DG.求证:△BHE≌△DGF.
- 1
24.(8分)在△ABC中,∠BAC=90°,AC=8cm,AB
(2)求△ABC 的面积.
25.(8分)如图,OE,OF 所在直线分别是△ABC 中AB,AC 边的中垂线(即垂直平分线),∠OBC,∠OCB的平分线相交于点I,试判定 OI 与BC 的位置关系,并给出证明.
26.(8分)如图,延长△ABC 的各边,使得BF=AC,AE=CD=AB.顺次连接点 D,E,F,得到的△DEF 为等边三角形.
(1)试说明△AEF≌△CDE.
(2)△ABC 是等边三角形吗 为什么
分类复习《轴对称图形》
一、1. M N AB 2.角平分线所在的直线 3.12cm 4.135° 5.50°,80°或 65°,65° 6.15 7.上 58.20 9.60° 10.25 cm
二、 11. C 12. B 13. D 14. C 15. B 16. C 17. B 18. B
三、19.略
20.
21.40°,70°,70°或 85°,47.5°,47.5°
22.王群正确,理由:∵AD=AC,∴∠ACD=∠ADC.又∵∠ACD=∠DCE+∠ACE,∠ADC=∠BCD+∠B,∴∠ACE+∠DCE=∠BCD+∠B. ① ∵BE=BC,∴∠CED=∠ECB.∵∠CED=∠ACE+∠H,∠ECB=∠BCD+∠DCE,∴∠BCD+∠DCE=∠ACE+∠A. ② ①式+②式,得2∠DCE=∠A+∠B.∵∠ACB=90°,∴∠A+∠B=90°,∴2∠DCE=90°,∠DCE=45°.
23.证明:由折叠可知 ∠GFD=∠C=90°,AB=BE,CD=FD.∵ABCD 是长方形,∴AB∥CD,AB=CD.∵AB∥CD,∴∠ABD=∠CDB.∴∠EBH=∠GDF.∵AB=CD,∴BE=DF.在△BHE 和△DGF 中, .△BHE≌△DGF(ASA).
24.(1)6cm (2)24 cm
25. OI⊥BC.证明:连接AO,延长 OI 交 BC 于点M.∵OE,OF 所在直线分别为AB,AC 的中垂线,∴OA=OB,OA=OC,∴OB=OC.又∵BI,CI 分别为∠OBC,∠OCB 的平分线,∴点 I 必在∠BOC 的平分线上,∴∠BOI=∠COI.在△BOM 和△COM 中, ∠CMO.又∵∠BMO+∠CMO=180°,∴∠BMO=∠CMO=90°,∴OI⊥BC.
26.(1)∵BF=AC,AB=AE,∴FA=EC.∵△DEF 为等边三角形,∴EF=DE.又∵AE=CD,∴△AEF≌△CDE.
(2)是等边三角形,理由:由(1)知,△AEF≌△CDE,∴∠FEA=∠EDC,∵△DEF 是等边三角形,∴∠DEF=60°.∵∠BCA=∠EDC+∠DEC=∠FEA+∠DEC=∠DEF,∴∠BCA=60°.同理,∠BAC=60°.∴△ABC 是等边三角形.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
