八年级数学下册试题 9.5三角形的中位线--苏科版(含答案)
文档属性
| 名称 | 八年级数学下册试题 9.5三角形的中位线--苏科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 120.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 15:15:46 | ||
图片预览



文档简介
9.5三角形的中位线
一、选择题.
1.如图,在△ABC中,D,E分别为AB,AC的中点,连接DE,若BC=10,则DE的长为( )
A.6 B.5 C. D.
2.如图,在△ABC中,BC=12,D、E分别是AB、AC的中点,F是DE上一点,DF=1,连接AF,CF,若∠AFC=90°,则AC的长度为( )
A.10 B.12 C.13 D.14
3.如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是( )
A.12m B.10m C.9m D.8m
4.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.8 B.7 C.6 D.5
5.如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长为( )
A.1 B. C. D.
6.如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米,若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是( )
A.22米 B.17米 C.14米 D.11米
7.如图,D,E,F分别是△ABC各边的中点,AH是高,若ED=6cm,那么HF的长为( )
A.5 cm B.6 cm C.10 cm D.不能确定
8.如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
A.3cm B.6cm C.9cm D.12cm
9.如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,若∠DAC=15°,∠ACB=87°,则∠FEG等于( )
A.39° B.18° C.72° D.36°
10.如图,在△ABC中,BD,CE是△ABC的中线,BD与CE相交于点O,点F,G分别是BO,CO的中点,连接AO.若要使得四边形DEFG是正方形,则需要满足条作( )
A.AO=BC B.AB⊥AC
C.AB=AC且AB⊥AC D.AO=BC且AO⊥BC
二、填空题
11.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=5,CD=3,EF=2,∠AFE=45°,则∠ADC的度数为 .
12.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别为AB、AC、AD的中点.若AB=6,则EF的长度为 .
13.在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,E为AC的中点,连按DE,则△CDE的面积为 .
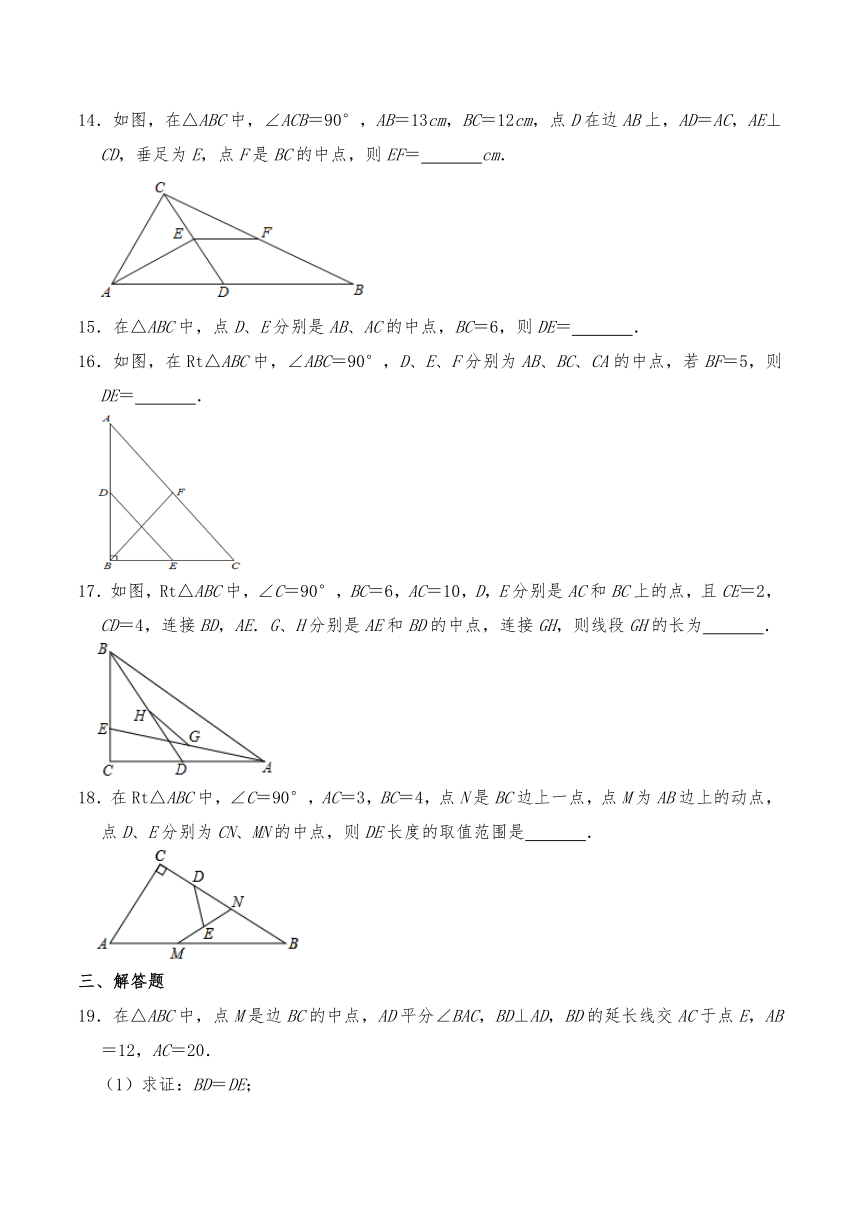
14.如图,在△ABC中,∠ACB=90°,AB=13cm,BC=12cm,点D在边AB上,AD=AC,AE⊥CD,垂足为E,点F是BC的中点,则EF= cm.
15.在△ABC中,点D、E分别是AB、AC的中点,BC=6,则DE= .
16.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE= .
17.如图,Rt△ABC中,∠C=90°,BC=6,AC=10,D,E分别是AC和BC上的点,且CE=2,CD=4,连接BD,AE.G、H分别是AE和BD的中点,连接GH,则线段GH的长为 .
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN、MN的中点,则DE长度的取值范围是 .
三、解答题
19.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
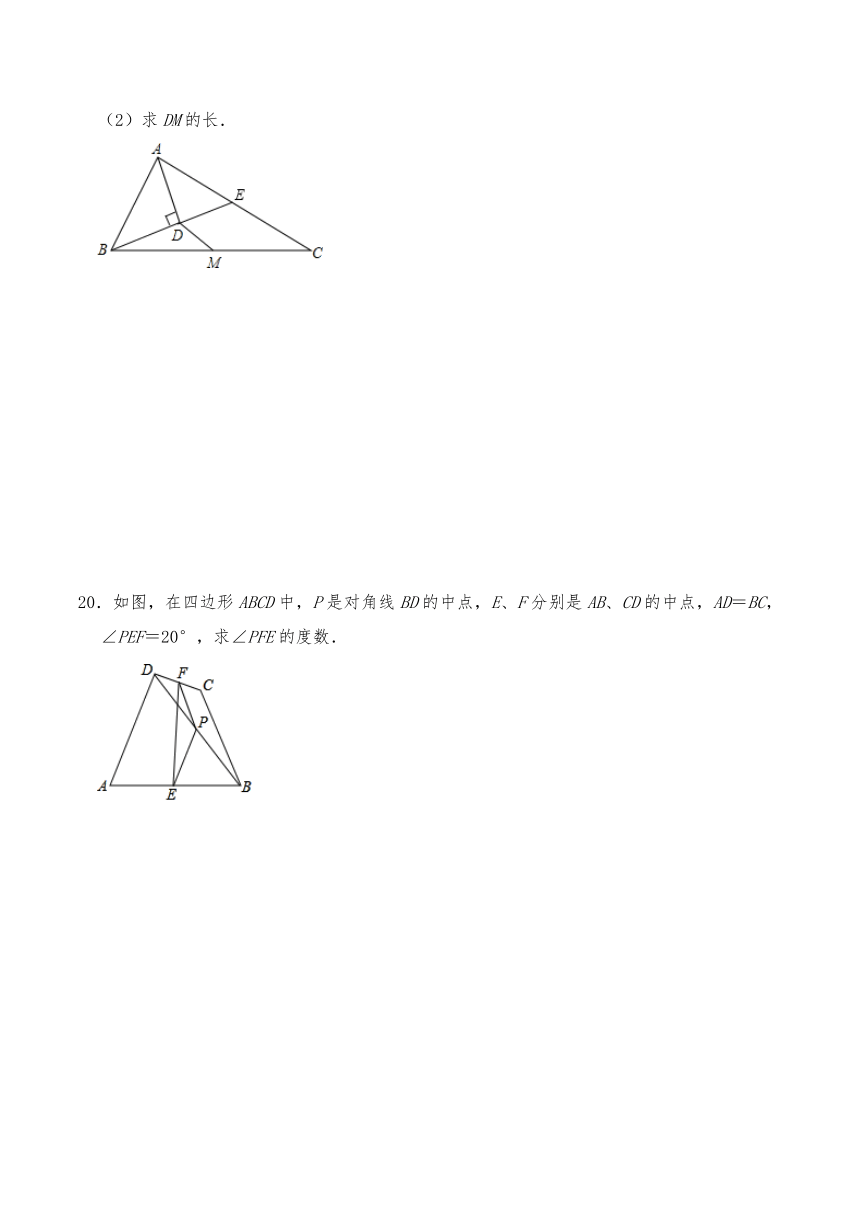
(2)求DM的长.
20.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=20°,求∠PFE的度数.
21.如图,在△ABC中,∠BAC=90°,DE是△ABC的中位线,AF是△ABC的中线.
求证DE=AF.
证法1:∵DE是△ABC的中位线,
∴DE= .
∵AF是△ABC的中线,∠BAC=90°,
∴AF= ,
∴DE=AF.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
22.如图,在△ABC中,AB=AC,点D是边AB的中点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
23.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
24.如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)AB=6,AC=4,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系?证明你的结论.
答案
一、选择题.
B.A.C.D.B.B.B.B.D.D.
二、填空题
11.135°.
12..
13..
14.4.
15.3.
16.5.
17..
18.DE≤2.
三、解答题
19.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DMEC=4.
20.∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PEAD,
同理,PFBC,
∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=20°.
21.证法1:∵DE是△ABC的中位线,
∴DEBC,
∵AF是△ABC的中线,∠BAC=90°,
∴AFBC,
∴DE=AF,
证法2:连接DF、EF,
∵DE是△ABC的中位线,AF是△ABC的中线,
∴DF、EF是△ABC的中位线,
∴DF∥AC,EF∥AB,
∴四边形ADFE是平行四边形,
∵∠BAC=90°,
∴四边形ADFE是矩形,
∴DE=AF.
故答案为:BC;BC.
22.(1)证明:∵AB=AC.
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F、G、H分别为BE、DE、BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FGBD,FHCE,
∴FG=FH;
(2)解:延长FG交AC于N,
∵FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,
∵FG⊥FH,
∴∠A=90°,
∴当∠A=90°时,FG⊥FH.
23.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
24.(1)∵AD是高,
∴∠ACB=∠ADC=90°,
在Rt△ADB中,E是AB的中点,
∴DEAB=3,AEAB=3,
同理可得,AF=DFAC=2,
∴四边形AEDF的周长=3+3+2+2=10;
(2)EF垂直平分AD,
理由如下:∵EA=ED,FA=FD,
∴EF是AD的垂直平分线.
一、选择题.
1.如图,在△ABC中,D,E分别为AB,AC的中点,连接DE,若BC=10,则DE的长为( )
A.6 B.5 C. D.
2.如图,在△ABC中,BC=12,D、E分别是AB、AC的中点,F是DE上一点,DF=1,连接AF,CF,若∠AFC=90°,则AC的长度为( )
A.10 B.12 C.13 D.14
3.如图,为了测量池塘边A、B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A、B分别是CD、CE的中点,若DE=18m,则线段AB的长度是( )
A.12m B.10m C.9m D.8m
4.如图,四边形ABCD中,∠A=90°,AB=8,AD=6,点M,N分别为线段BC,AB上的动点(含端点,但点M不与点B重合),点E,F分别为DM,MN的中点,则EF长度的最大值为( )
A.8 B.7 C.6 D.5
5.如图.在△ABC中,∠ACB=60°,AC=1,D是边AB的中点,E是边BC上一点.若DE平分△ABC的周长,则DE的长为( )
A.1 B. C. D.
6.如图是一块等腰三角形空地ABC,已知点D,E分别是边AB,AC的中点,量得AC=10米,AB=BC=6米,若用篱笆围成四边形BCED来放养小鸡,则需要篱笆的长是( )
A.22米 B.17米 C.14米 D.11米
7.如图,D,E,F分别是△ABC各边的中点,AH是高,若ED=6cm,那么HF的长为( )
A.5 cm B.6 cm C.10 cm D.不能确定
8.如图,平行四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
A.3cm B.6cm C.9cm D.12cm
9.如图,在四边形ABCD中,AD=BC,E、F、G分别是AB、CD、AC的中点,若∠DAC=15°,∠ACB=87°,则∠FEG等于( )
A.39° B.18° C.72° D.36°
10.如图,在△ABC中,BD,CE是△ABC的中线,BD与CE相交于点O,点F,G分别是BO,CO的中点,连接AO.若要使得四边形DEFG是正方形,则需要满足条作( )
A.AO=BC B.AB⊥AC
C.AB=AC且AB⊥AC D.AO=BC且AO⊥BC
二、填空题
11.如图,在四边形ABCD中,点E、F分别是边AB、AD的中点,BC=5,CD=3,EF=2,∠AFE=45°,则∠ADC的度数为 .
12.如图,在Rt△ABC中,∠ACB=90°,D、E、F分别为AB、AC、AD的中点.若AB=6,则EF的长度为 .
13.在△ABC中,AB=AC=5,BC=6,AD平分∠BAC交BC于点D,E为AC的中点,连按DE,则△CDE的面积为 .
14.如图,在△ABC中,∠ACB=90°,AB=13cm,BC=12cm,点D在边AB上,AD=AC,AE⊥CD,垂足为E,点F是BC的中点,则EF= cm.
15.在△ABC中,点D、E分别是AB、AC的中点,BC=6,则DE= .
16.如图,在Rt△ABC中,∠ABC=90°,D、E、F分别为AB、BC、CA的中点,若BF=5,则DE= .
17.如图,Rt△ABC中,∠C=90°,BC=6,AC=10,D,E分别是AC和BC上的点,且CE=2,CD=4,连接BD,AE.G、H分别是AE和BD的中点,连接GH,则线段GH的长为 .
18.在Rt△ABC中,∠C=90°,AC=3,BC=4,点N是BC边上一点,点M为AB边上的动点,点D、E分别为CN、MN的中点,则DE长度的取值范围是 .
三、解答题
19.在△ABC中,点M是边BC的中点,AD平分∠BAC,BD⊥AD,BD的延长线交AC于点E,AB=12,AC=20.
(1)求证:BD=DE;
(2)求DM的长.
20.如图,在四边形ABCD中,P是对角线BD的中点,E、F分别是AB、CD的中点,AD=BC,∠PEF=20°,求∠PFE的度数.
21.如图,在△ABC中,∠BAC=90°,DE是△ABC的中位线,AF是△ABC的中线.
求证DE=AF.
证法1:∵DE是△ABC的中位线,
∴DE= .
∵AF是△ABC的中线,∠BAC=90°,
∴AF= ,
∴DE=AF.
请把证法1补充完整,并用不同的方法完成证法2.
证法2:
22.如图,在△ABC中,AB=AC,点D是边AB的中点,DE∥BC交AC于点E,连接BE,点F、G、H分别为BE、DE、BC的中点.
(1)求证:FG=FH;
(2)当∠A为多少度时,FG⊥FH?并说明理由.
23.已知:△ABC中,D是BC上的一点,E、F、G、H分别是BD、BC、AC、AD的中点,
求证:EG、HF互相平分.
24.如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)AB=6,AC=4,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系?证明你的结论.
答案
一、选择题.
B.A.C.D.B.B.B.B.D.D.
二、填空题
11.135°.
12..
13..
14.4.
15.3.
16.5.
17..
18.DE≤2.
三、解答题
19.(1)证明:∵AD平分∠BAC,
∴∠BAD=∠DAE.
∵AD⊥BD,
∴∠ADB=∠ADE=90°.
在△ADB与△ADE中,
∴△ADB≌△ADE,
∴BD=DE.
(2)∵△ADB≌△ADE,
∴AE=AB=12,
∴EC=AC﹣AE=8.
∵M是BC的中点,BD=DE,
∴DMEC=4.
20.∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PEAD,
同理,PFBC,
∵AD=BC,
∴PE=PF,
∴∠PFE=∠PEF=20°.
21.证法1:∵DE是△ABC的中位线,
∴DEBC,
∵AF是△ABC的中线,∠BAC=90°,
∴AFBC,
∴DE=AF,
证法2:连接DF、EF,
∵DE是△ABC的中位线,AF是△ABC的中线,
∴DF、EF是△ABC的中位线,
∴DF∥AC,EF∥AB,
∴四边形ADFE是平行四边形,
∵∠BAC=90°,
∴四边形ADFE是矩形,
∴DE=AF.
故答案为:BC;BC.
22.(1)证明:∵AB=AC.
∴∠ABC=∠ACB,
∵DE∥BC,
∴∠ADE=∠ABC,∠AED=∠ACB,
∴∠ADE=∠AED,
∴AD=AE,
∴DB=EC,
∵点F、G、H分别为BE、DE、BC的中点,
∴FG是△EDB的中位线,FH是△BCE的中位线,
∴FGBD,FHCE,
∴FG=FH;
(2)解:延长FG交AC于N,
∵FG是△EDB的中位线,FH是△BCE的中位线,
∴FH∥AC,FN∥AB,
∵FG⊥FH,
∴∠A=90°,
∴当∠A=90°时,FG⊥FH.
23.证明:连接EH,GH,GF,
∵E、F、G、H分别是BD、BC、AC、AD的中点,
∴AB∥EH∥GF,GH∥BC∥BF.
∴四边形EHGF为平行四边形.
∵GE,HF分别为其对角线,
∴EG、HF互相平分.
24.(1)∵AD是高,
∴∠ACB=∠ADC=90°,
在Rt△ADB中,E是AB的中点,
∴DEAB=3,AEAB=3,
同理可得,AF=DFAC=2,
∴四边形AEDF的周长=3+3+2+2=10;
(2)EF垂直平分AD,
理由如下:∵EA=ED,FA=FD,
∴EF是AD的垂直平分线.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
