九年级数学下册试题 第五章《二次函数》单元复习-苏科版(含答案)
文档属性
| 名称 | 九年级数学下册试题 第五章《二次函数》单元复习-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 177.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 15:13:13 | ||
图片预览




文档简介
第五章《二次函数》单元复习
一.选择题
1. 抛物线y=x2+ax+3的对称轴为直线x=1.若关于x的方程x2+ax+3﹣t=0(t为实数)在﹣2<x<3的范围内有实数根,则t的取值范围是( )
A.6<t<11 B.t≥2 C.2≤t<11 D.2≤t<6
2. 已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=﹣2时,函数图象与x轴没有交点
B.若a<0,函数图象的顶点始终在x轴的下方
C.若a>0,则当x≥1时,y随x的增大而减小
D.不论a为何值,函数图象必经过(2,﹣1)
3. 对于函数y=ax2﹣(2a+1)x﹣3a+1(a是常数),有下列说法:
①函数图象与坐标轴总有三个不同的交点;
②当x<1时,不是y随x的增大而增大就是y随x的增大而减小;
③若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.
其中错误的说法是( )
A.① B.①② C.②③ D.①③
4. 二次函数y=ax2+bx+c的图象如图所示,下列结论:(1)b<2a;(2)a+c﹣b>0;(3)b>c>a;(4)b2+2ac<3ab.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
5. 已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法中:①abc<0;②2a+b=0;③当﹣1<x<3时,y>0;④a﹣b+c<0;⑤2c﹣3b>0.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
6. 一条抛物线与x轴相交于A、B两点(点A在点B的左侧),若点M、N的坐标分别为(﹣1,﹣2)、(1,﹣2),抛物线顶点P在线段MN上移动.点B的横坐标的最大值为3,则点A的横坐标的最小值为( )
A.﹣3 B.﹣1 C.1 D.3
7. 关于x的二次函数y=﹣2x2+4x+m2+2m,下列说法正确的是( )
A.该二次函数的图象与x轴始终有两个交点
B.当x>0时,y随x的增大而增大
C.当该二次函数的图象经过原点时,m=﹣2
D.该二次函数的顶点的纵坐标无最小值
8. 在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣1(m>0)与x轴的交点为A,B.若横、纵坐标都是整数的点叫做整点,当抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,可得m的取值范围为( )
A.m B.m C.0<m D.0<m
9. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点在B(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论不正确的是( )
A.9a+3b+c=0 B.4b﹣3c>0 C.4ac﹣b2<﹣4a D.a
10.如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,顶点P(m,n)给出下列结论:①2a+c<0;②若(,y1),(,y2),(,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n时,△ABP为等腰直角三角形,其中正确的结论是( )
A.①② B.①③ C.②③ D.②④
11.已知函数f(x)=x2﹣2ax+5,当x≤2时,函数值随x增大而减小,且对任意的1≤x1≤a+1和1≤x2≤a+1,x1,x2相应的函数值y1,y2总满足|y1﹣y2|≤4,则实数a的取值范围是( )
A.﹣1≤a≤3 B.﹣1≤a≤2 C.2≤a≤3 D.2≤a≤4
12.对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点.若二次函数y=x2+2x+c(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是( )
A.c<﹣3 B.﹣3<c<﹣2 C.﹣2<c D.c
13.已知二次函数y=x2﹣bx+a﹣3的图象与x轴有交点,对称轴位于y轴左侧,则当关于a,b的代数式(a﹣6)2+b2有最小值时,该二次函数的顶点坐标为( )
A.(1,0) B.(1,2) C.(﹣1,0) D.(﹣1,2)
14.已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数,抛物线与x轴交于A、B两点(点A在点B的左侧).给出下列4个结论:①不论m为何值,该抛物线与x轴一定有两个公共点;②不论m为何值,该抛物线与y轴一定交于正半轴;③抛物线上有一个动点P,满足S△PAB=n的点有3个时,则n;④若0<x时y<0,则m<0;其中,正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题
15.飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是s=96t﹣1.2t2,那么飞机着陆后滑行 米停下.
16.二次函数y=﹣(x+1)2﹣2的最大值是 .
17.当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m= .
18.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是 .
19.已知点A(0,2)与点B(2,4)的坐标,抛物线y=ax2﹣6ax+9a+1与线段AB有交点,则a的取值范围是 .
20.如图,在平面直角坐标系中,点A的坐标为(0,2),点B的坐标为(4,2).若抛物线y(x﹣h)2+k(h、k为常数)与线段AB交于C、D两点,且CDAB,则k的值为 .
21.抛物线y=ax2+bx+c经过A(﹣1,3),B(2,3),则关于x的一元二次方程a(x﹣2)2﹣3=2b﹣bx﹣c的解为 .
22.若整数a使关于x的二次函数y=(a﹣1)x2﹣(2a+3)x+a+2的图象在x轴的下方,且使关于x的分式方程2有负整数解,则所有满足条件的整数a的和为 .
23.已知二次函数y=ax2+bx﹣6(a>0)的图象与x轴的交点A坐标为(n,0),顶点D的坐标为(m,t),若m+n=0,则t=
24.已知抛物线y=x2+mx+n经过点(2,﹣1),且与x轴交于A(a,0),B(b,0)两点,若点P为该抛物线的顶点,则使△PAB面积最小时抛物线的解析式为 .
25.对于一个函数,如果它的自变量x与函数值y满足:当﹣1≤x≤1时,﹣1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=﹣x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,﹣1)和点B(﹣1,1),则a的取值范围是 .
三.解答题
26.学校计划购买一批钢笔和笔记本,用以奖励优秀学生,获得一、二等奖的学生分别奖励一支钢笔、一本笔记本;已知购买2支钢笔和3本笔记本共38元,购买4支钢笔和5本笔记本共70元.
(1)钢笔、笔记本的单价分别为多少元?
(2)经与商家协商,购买钢笔超过30支时,每增加1支,单价降低0.1元,笔记本按原价销售,学校计划奖励一、二等奖学生共计100人,其中一等奖的人数不少于30人,且不超过50人,当这次奖励一等奖学生多少人时,购买奖品总金额最少,最少为多少元?
27.饮料厂生产某品牌的饮料成本是每瓶5元,每天的生产量不超过9000瓶.根据市场调查,以单价8元批发给经销商,经销商每天愿意经销5000瓶,并且表示单价每降价0.1元,经销商每天愿意多经销500瓶.
(1)求出饮料厂每天的利润y(元)与批发单价x(元)之间的函数关系式;
(2)批发单价定为多少元时,饮料厂每天的利润最大,最大利润是多少元?
(3)如果该饮料厂要使每天的利润不低于18750元,且每天的总成本不超过42500元,那么批发单价应控制在什么范围?(每天的总成本=每瓶的成本×每天的经销量)
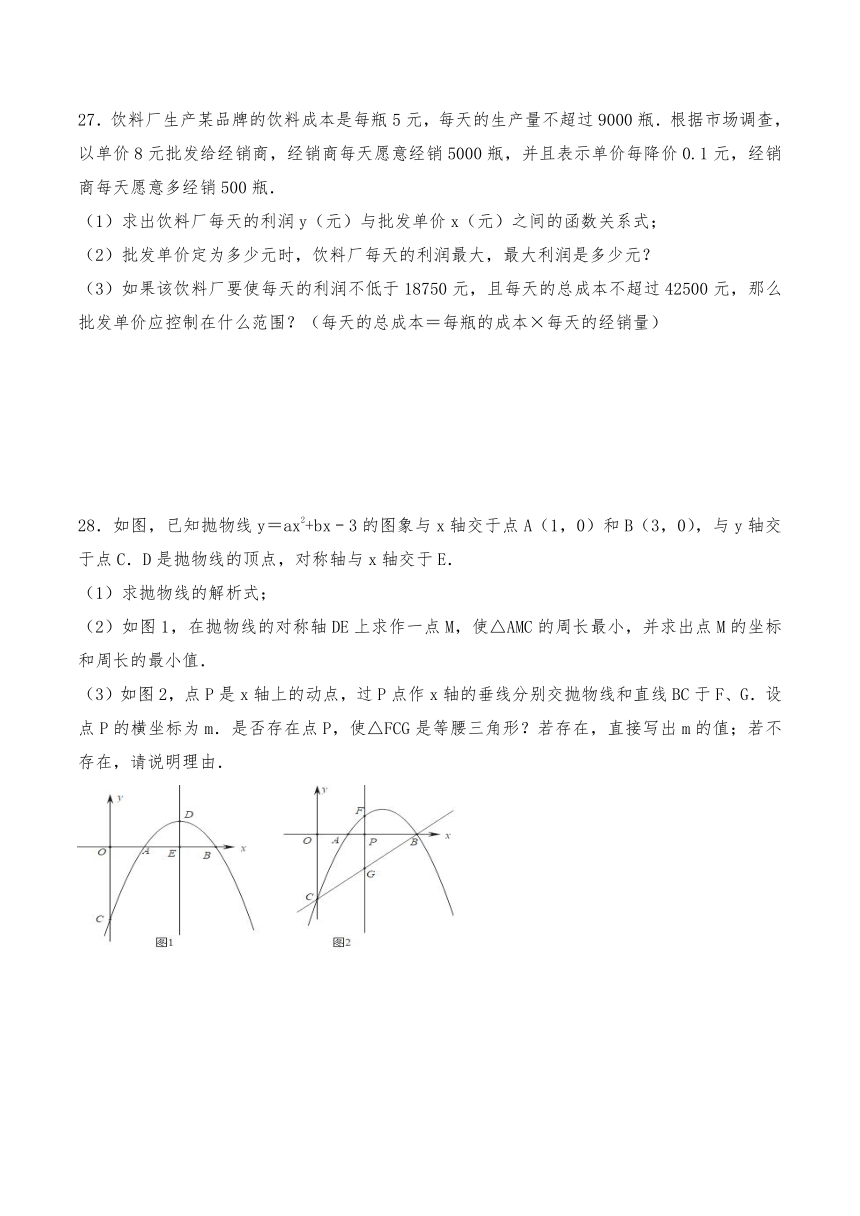
28.如图,已知抛物线y=ax2+bx﹣3的图象与x轴交于点A(1,0)和B(3,0),与y轴交于点C.D是抛物线的顶点,对称轴与x轴交于E.
(1)求抛物线的解析式;
(2)如图1,在抛物线的对称轴DE上求作一点M,使△AMC的周长最小,并求出点M的坐标和周长的最小值.
(3)如图2,点P是x轴上的动点,过P点作x轴的垂线分别交抛物线和直线BC于F、G.设点P的横坐标为m.是否存在点P,使△FCG是等腰三角形?若存在,直接写出m的值;若不存在,请说明理由.
29.某地摊上的一种玩具,已知其进价为50元/个,试销阶段发现将售价定为80元/个时,每天可销售20个,后来为了扩大销售量,适当降低了售价,销售量y(个)与降价x(元)的关系如图所示.
(1)求销量y与降价x之间的关系式;
(2)该玩具每个降价多少元,可以恰好获得750元的利润?
(3)若要使得平均每天销售这种玩具的利润W最大,则每个玩具应该降价多少元?最大的利润W为多少元?
30.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.
(1)求抛物线y=ax2+2x+c的解析式;
(2)点D为抛物线上对称轴右侧、x轴上方一点,DE⊥x轴于点E,DF∥AC交抛物线对称轴于点F,求DE+DF的最大值;
(3)①在拋物线上是否存在点P,使以点A,P,C为顶点的三角形,是以AC为直角边的直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
②点Q在抛物线对称轴上,其纵坐标为t,请直接写出△ACQ为锐角三角形时t的取值范围.
31.如图(1),抛物线y=ax2+bx经过A和B(3,﹣3)两点,点A在x轴的正半轴,且OA=4.
(1)求抛物线的解析式;
(2)若点M是抛物线上一动点,且在直线OB的下方(不与O、B重合),过M作MK⊥x轴,交直线BO于点N,过M作MP∥x轴,交直线BO于点P,求出△MNP周长的最大值及周长取得最大值时点M的坐标;
(3)如图(2),过B作BD⊥y轴于点D,交抛物线于点C,连接OC,在抛物线上是否存在点Q使得S△OCD:S△OCQ=3:2,若存在,请求出点Q的坐标,若不存在,请说明理由.
32.已知抛物线与x轴交于点A(﹣2,0)、B(3,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)如图1,点P是抛物线上位于第一象限内的一点,当四边形ABPC的面积最大时,求出四边形ABPC的面积最大值及此时点P的坐标.
(3)如图2,将抛物线向右平移个单位,再向下平移2个单位.记平移后的抛物线为y',若抛物线y'与原抛物线对称轴交于点Q.点E是新抛物线y'对称轴上一动点,在(2)的条件下,当△PQE是等腰三角形时,求点E的坐标.
答案
一.选择题
C.D.B.B.B.A.A.A.D.D.C.C.C.B.
二.填空题
15.1920.
16.﹣2.
17.10.
18.s≥9.
19.a≤3.
20.k.
21.1或4.
22.﹣16.
23.﹣8.
24.y=x2﹣4x+3.
25.a<0或0<a.
三.解答题
26.(1)设钢笔、笔记本的单价分别为x元、y元,根据题意,得,
解这个方程组,得,
所以钢笔、笔记本的单价分别为10元、6元;
(2)这次奖励一等奖的学生为a人,购买奖品总余额为w元,
则w=a[10﹣0.1(a﹣30)]+6(100﹣a)=﹣0.1a2+7a+600=﹣0.1(a﹣35)2+722.5,
∵30≤a≤50
∴a=50时w=﹣0.1×(50﹣35)2+722.5=700(元)最少,
所以这次奖励学生一等奖为50人时,购买奖品总额最少,最少为700元.
27.(1)根据题意,得:5000x2+70000x﹣225000=﹣5000(x﹣7)2+20000,
答:y与x的函数关系式为y=﹣5000x2+70000x﹣225000;
(2)由题意,得,
解得x≥7.2,
∵a=﹣5000<0,
∴抛物线开口向下,对称轴为直线x=7,
∵x≥7.2,
∴此时函数图象在对称轴的右侧,y随x的增大而减小,
∴x=7.2(元)时,y取得最大值,ymax=19800(元);
答:当批发单价为7.2元时,饮料厂每天的利润最大,最大利润是19800元;
(3)根据题意得﹣5000x2+70000x﹣225000=18750,
解得:x1=6.5,x2=7.5,
∵抛物线开口向下,
∴当6.5≤x≤7.5时,每天的利润不低于18700元,
∵每天的总成本不超过42500元,
∴,
解得x≥7.3,
∴7.3≤x≤7.5,
答:批发单价应控制在7.3元到7.5元之间.
28.(1)将点A、B的坐标代入抛物线表达式得:,
解得,
∴抛物线的解析式为:y=﹣x2+4x﹣3;
(2)如下图,连接BC交DE于点M,此时MA+MC最小,
又因为AC是定值,所以此时△AMC的周长最小.
由题意可知OB=OC=3,OA=1,
∴BC3,同理AC,
∴此时△AMC的周长=AC+AM+MC=AC+BC3;
∵DE是抛物线的对称轴,与x轴交点A(1,0)和B(3,0),
∴AE=BE=1,对称轴为 x=2,
由OB=OC,∠BOC=90°得∠OBC=45°,
∴EB=EM=1,
又∵点M在第四象限,在抛物线的对称轴上,
∴M(2,﹣1);
(3)存在这样的点P,使△FCG是等腰三角形.
∵点P的横坐标为m,故点F(m,﹣m2+4m﹣3),点G(m,m﹣3),
则FG2=(﹣m2+4m﹣3)2,CF2=(m2﹣3m)2,GC2=2m2,
当FG=FC时,则(﹣m2+4m﹣3)2=(m2﹣3m)2,解得m=0(舍去)或4;
当GF=GC时,同理可得m=0(舍去)或3;
当FC=GC时,同理可得m=0(舍去)或5,
综上,m=5或m=4或或3.
29.(1)设销量y与降价x之间的关系式y=kx+b,
将点(2,24)、(4,28)代入上式得,解得,
故销量y与降价x之间的关系式y=2x+20;
(2)由题意得:(80﹣x﹣50)(2x+20)=750,
解得x=5或15(元),
故该玩具每个降价5元或15元,可以恰好获得750元的利润;
(3)由题意得:W=(80﹣x﹣50)(2x+20)=﹣2(x﹣10)2+800,
∵﹣2<0,
故当x=10(元)时,W的最大值为800(元).
30.(1)设抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∴﹣2a=2,解得a=﹣1,
∴抛物线解析式为y=﹣x2+2x+3;
(2)当x=0时,y=﹣x2+2x+3=3,则C(0,3),
设直线AC的解析式为y=px+q,把A(﹣1,0),
C(0,3)代入得,解得,
∴直线AC的解析式为y=3x+3,
如图1,过D作DG垂直抛物线对称轴于点G,设D(x,﹣x2+2x+3),
∵DF∥AC,
∴∠DFG=∠ACO,
而抛物线对称轴为x=1,
∴DG=x﹣1,DF(x﹣1),
∴DE+DF=﹣x2+2x+3(x﹣1)=﹣x2+(2)x+3(x)2,
∵﹣1<0,
∴当x,DE+DF有最大值为;
(3)①存在;
如图2,过点C作AC的垂线交抛物线于点P1,
∵直线AC的解析式为y=3x+3,
则直线AC倾斜角的正切值为3,则直线P1C倾斜角的正切值为,
∴直线P1C的解析式可设为yx+m,把C(0,3)代入得m=3,
∴直线P1C的解析式为yx+3,解方程组,
解得,
则此时P1点坐标为(,);
过点A作AC的垂线交抛物线于P2,
同理可设直线AP2的解析式可设为yx+n,
把A(﹣1,0)代入上式并解得n,
∴直线PC的解析式为yx,
解方程组,解得,
则此时P2点坐标为(,),
综上所述,符合条件的点P的坐标为(,)或(,);
②答:t<1或2<t.
如图3,抛物线y=﹣x2+2x+3对称轴为直线x=1,过点C作CQ1⊥AC交对称轴于Q1,过点A作AQ2⊥AC交对称轴于Q2,
∵A(﹣1,0),C(0,3),
∴直线AC解析式为y=3x+3,
∵CQ1⊥AC,
∴直线CQ1解析式为yx+3,
令x=1,得y1+3,
∴Q1(1,);
∵AQ2⊥AC,
∴直线AQ2解析式为y═x,令x=1,得y1,
∵∠AQC=90°时,AQ2+CQ2=AC2,
∴(﹣1﹣1)2+t2+(1﹣0)2+(t﹣3)2=()2,解得:t1=1,t2=2,
∴当1≤t≤2时,∠AQC≥90°,
∵△ACQ为锐角三角形,点Q(1,t)必须在线段Q1Q2上(不含端点Q1、Q2),
∴t<1或2<t.
31.(1)∵点A在x轴的正半轴,且OA=4,
∴点A(4,0),
∵抛物线y=ax2+bx经过A(4,0),B(3,﹣3),
∴,
解得,
∴抛物线解析式为:y=x2﹣4x;
(2)∵点B(3,﹣3),
∴直线OB解析式为y=﹣x,
设点M(m,m2﹣4m),
∴点N(m,﹣m),K(m,0),
∴OK=KN,
∴∠KON=∠KNO=45°,
∵MP∥x轴,
∴∠MPN=∠KON=45°,
∴∠MPN=∠KNO=∠MNP=45°,
∴MP=MN,
∴NPMN,
∵△MNP的周长=MN+MP+NP=2MNMN=2(4m﹣m2﹣m)(4m﹣m2﹣m)=(2)(3m﹣m2)=﹣(2)[(m)2],
∴当m时,△MNP的周长的最大值为,
此时点M坐标为(,);
(3)存在点Q使得S△OCD:S△OCQ=3:2,
理由如下:
如图(2),在线段CB上截取CE,连接OE,过点E作OC的平行线交抛物线于点Q,连接OQ,
∵S△OCECE×OD3=1,且OC∥QE,
∴S△OCQ=1,
∵BD⊥y轴,
∴OD=3,点C纵坐标为﹣3,
∴﹣3=x2﹣4x,
∴x1=1,x2=3,
∴点C(1,﹣3),
∴CD=1,
∴S△OCD1×3,
∴S△OCD:S△OCQ=3:2,
∵点O(0,0),点C(1,﹣3),
∴直线OC解析式为:y=﹣3x,
∵CE,
∴点E(,﹣3),
∵OC∥EQ,
∴设EQ的解析式为:y=﹣3x+b,
∴﹣3=﹣3b,
∴b=2,
∴EQ的解析式为:y=﹣3x+2,
联立方程组可得,
∴,,
∴点Q坐标为(﹣1,5)或(2,﹣4).
32.(1)∵抛物线与x轴交于点A(﹣2,0)、B(3,0),
∴可设抛物线的解析式为:y=a(x+2)(x﹣3)(a≠0),
把C(0,4)代入y=a(x+2)(x﹣3)(a≠0)中,得
4=﹣6a,
∴a,
∴抛物线的解析式为:y,
即y;
(2)设P点的坐标为(t,),过点P作PM⊥x轴,与BC交于点M,如图1,
设直线BC的解析式为y=kx+b(k≠0),则
,
解得,
∴直线BC的解析式为:y,
∴M(t,),
∴,
∴t2+3t,
,
,
∴S四边形ABPC=S△AOC+S△BOC+S△BPC,
∴当t时,S四边形ABPC取最大值,
∴此时P点的坐标为(,);
(3)∵将抛物线向右平移个单位,再向下平移2个单位.记平移后的抛物线为y',
∴y′的解析式为y,即y,
∴抛物线y′的对称轴为x=1,
∵抛物线y,
∴抛物线y的对称轴为直线x,
把x代入y中,得y=2,
∴Q点的坐标为(,2),
设E的坐标为(1,n)
①当PE=QE时,则PE2=QE2,
即,
解得,n,
∴E(1,),
②当PQ=QE时,则PQ2=QE2,
即,
解得,n=2±,
∴E点的坐标为(1,2)或(1,2);
③当PQ=PE时,则PQ2=PE2,
即,
解得,n,
∴点E的坐标为(1,)或(1,).
综上,当△PQE是等腰三角形时,点E的坐标为(1,)或(1,2)或(1,2)或(1,)或(1,).
一.选择题
1. 抛物线y=x2+ax+3的对称轴为直线x=1.若关于x的方程x2+ax+3﹣t=0(t为实数)在﹣2<x<3的范围内有实数根,则t的取值范围是( )
A.6<t<11 B.t≥2 C.2≤t<11 D.2≤t<6
2. 已知函数y=ax2﹣2ax﹣1(a是常数,a≠0),下列结论正确的是( )
A.当a=﹣2时,函数图象与x轴没有交点
B.若a<0,函数图象的顶点始终在x轴的下方
C.若a>0,则当x≥1时,y随x的增大而减小
D.不论a为何值,函数图象必经过(2,﹣1)
3. 对于函数y=ax2﹣(2a+1)x﹣3a+1(a是常数),有下列说法:
①函数图象与坐标轴总有三个不同的交点;
②当x<1时,不是y随x的增大而增大就是y随x的增大而减小;
③若函数有最大值,则最大值必为正数,若函数有最小值,则最小值必为负数.
其中错误的说法是( )
A.① B.①② C.②③ D.①③
4. 二次函数y=ax2+bx+c的图象如图所示,下列结论:(1)b<2a;(2)a+c﹣b>0;(3)b>c>a;(4)b2+2ac<3ab.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
5. 已知二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,下列说法中:①abc<0;②2a+b=0;③当﹣1<x<3时,y>0;④a﹣b+c<0;⑤2c﹣3b>0.其中正确结论的个数是( )
A.2 B.3 C.4 D.5
6. 一条抛物线与x轴相交于A、B两点(点A在点B的左侧),若点M、N的坐标分别为(﹣1,﹣2)、(1,﹣2),抛物线顶点P在线段MN上移动.点B的横坐标的最大值为3,则点A的横坐标的最小值为( )
A.﹣3 B.﹣1 C.1 D.3
7. 关于x的二次函数y=﹣2x2+4x+m2+2m,下列说法正确的是( )
A.该二次函数的图象与x轴始终有两个交点
B.当x>0时,y随x的增大而增大
C.当该二次函数的图象经过原点时,m=﹣2
D.该二次函数的顶点的纵坐标无最小值
8. 在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+m﹣1(m>0)与x轴的交点为A,B.若横、纵坐标都是整数的点叫做整点,当抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,可得m的取值范围为( )
A.m B.m C.0<m D.0<m
9. 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点在B(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1,下列结论不正确的是( )
A.9a+3b+c=0 B.4b﹣3c>0 C.4ac﹣b2<﹣4a D.a
10.如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)与x轴交于A,B两点,顶点P(m,n)给出下列结论:①2a+c<0;②若(,y1),(,y2),(,y3)在抛物线上,则y1>y2>y3;③关于x的方程ax2+bx+k=0有实数解,则k>c﹣n;④当n时,△ABP为等腰直角三角形,其中正确的结论是( )
A.①② B.①③ C.②③ D.②④
11.已知函数f(x)=x2﹣2ax+5,当x≤2时,函数值随x增大而减小,且对任意的1≤x1≤a+1和1≤x2≤a+1,x1,x2相应的函数值y1,y2总满足|y1﹣y2|≤4,则实数a的取值范围是( )
A.﹣1≤a≤3 B.﹣1≤a≤2 C.2≤a≤3 D.2≤a≤4
12.对于一个函数:当自变量x取a时,其函数值y也等于a,我们称a为这个函数的不动点.若二次函数y=x2+2x+c(c为常数)有两个不相等且都小于1的不动点,则c的取值范围是( )
A.c<﹣3 B.﹣3<c<﹣2 C.﹣2<c D.c
13.已知二次函数y=x2﹣bx+a﹣3的图象与x轴有交点,对称轴位于y轴左侧,则当关于a,b的代数式(a﹣6)2+b2有最小值时,该二次函数的顶点坐标为( )
A.(1,0) B.(1,2) C.(﹣1,0) D.(﹣1,2)
14.已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数,抛物线与x轴交于A、B两点(点A在点B的左侧).给出下列4个结论:①不论m为何值,该抛物线与x轴一定有两个公共点;②不论m为何值,该抛物线与y轴一定交于正半轴;③抛物线上有一个动点P,满足S△PAB=n的点有3个时,则n;④若0<x时y<0,则m<0;其中,正确的结论个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题
15.飞机着陆后滑行的距离s(单位:米)与滑行的时间t(单位:秒)之间的函数关系式是s=96t﹣1.2t2,那么飞机着陆后滑行 米停下.
16.二次函数y=﹣(x+1)2﹣2的最大值是 .
17.当﹣1≤x≤3时,二次函数y=x2﹣4x+5有最大值m,则m= .
18.若实数x,y满足x+y2=3,设s=x2+8y2,则s的取值范围是 .
19.已知点A(0,2)与点B(2,4)的坐标,抛物线y=ax2﹣6ax+9a+1与线段AB有交点,则a的取值范围是 .
20.如图,在平面直角坐标系中,点A的坐标为(0,2),点B的坐标为(4,2).若抛物线y(x﹣h)2+k(h、k为常数)与线段AB交于C、D两点,且CDAB,则k的值为 .
21.抛物线y=ax2+bx+c经过A(﹣1,3),B(2,3),则关于x的一元二次方程a(x﹣2)2﹣3=2b﹣bx﹣c的解为 .
22.若整数a使关于x的二次函数y=(a﹣1)x2﹣(2a+3)x+a+2的图象在x轴的下方,且使关于x的分式方程2有负整数解,则所有满足条件的整数a的和为 .
23.已知二次函数y=ax2+bx﹣6(a>0)的图象与x轴的交点A坐标为(n,0),顶点D的坐标为(m,t),若m+n=0,则t=
24.已知抛物线y=x2+mx+n经过点(2,﹣1),且与x轴交于A(a,0),B(b,0)两点,若点P为该抛物线的顶点,则使△PAB面积最小时抛物线的解析式为 .
25.对于一个函数,如果它的自变量x与函数值y满足:当﹣1≤x≤1时,﹣1≤y≤1,则称这个函数为“闭函数”.例如:y=x,y=﹣x均是“闭函数”.已知y=ax2+bx+c(a≠0)是“闭函数”,且抛物线经过点A(1,﹣1)和点B(﹣1,1),则a的取值范围是 .
三.解答题
26.学校计划购买一批钢笔和笔记本,用以奖励优秀学生,获得一、二等奖的学生分别奖励一支钢笔、一本笔记本;已知购买2支钢笔和3本笔记本共38元,购买4支钢笔和5本笔记本共70元.
(1)钢笔、笔记本的单价分别为多少元?
(2)经与商家协商,购买钢笔超过30支时,每增加1支,单价降低0.1元,笔记本按原价销售,学校计划奖励一、二等奖学生共计100人,其中一等奖的人数不少于30人,且不超过50人,当这次奖励一等奖学生多少人时,购买奖品总金额最少,最少为多少元?
27.饮料厂生产某品牌的饮料成本是每瓶5元,每天的生产量不超过9000瓶.根据市场调查,以单价8元批发给经销商,经销商每天愿意经销5000瓶,并且表示单价每降价0.1元,经销商每天愿意多经销500瓶.
(1)求出饮料厂每天的利润y(元)与批发单价x(元)之间的函数关系式;
(2)批发单价定为多少元时,饮料厂每天的利润最大,最大利润是多少元?
(3)如果该饮料厂要使每天的利润不低于18750元,且每天的总成本不超过42500元,那么批发单价应控制在什么范围?(每天的总成本=每瓶的成本×每天的经销量)
28.如图,已知抛物线y=ax2+bx﹣3的图象与x轴交于点A(1,0)和B(3,0),与y轴交于点C.D是抛物线的顶点,对称轴与x轴交于E.
(1)求抛物线的解析式;
(2)如图1,在抛物线的对称轴DE上求作一点M,使△AMC的周长最小,并求出点M的坐标和周长的最小值.
(3)如图2,点P是x轴上的动点,过P点作x轴的垂线分别交抛物线和直线BC于F、G.设点P的横坐标为m.是否存在点P,使△FCG是等腰三角形?若存在,直接写出m的值;若不存在,请说明理由.
29.某地摊上的一种玩具,已知其进价为50元/个,试销阶段发现将售价定为80元/个时,每天可销售20个,后来为了扩大销售量,适当降低了售价,销售量y(个)与降价x(元)的关系如图所示.
(1)求销量y与降价x之间的关系式;
(2)该玩具每个降价多少元,可以恰好获得750元的利润?
(3)若要使得平均每天销售这种玩具的利润W最大,则每个玩具应该降价多少元?最大的利润W为多少元?
30.如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.
(1)求抛物线y=ax2+2x+c的解析式;
(2)点D为抛物线上对称轴右侧、x轴上方一点,DE⊥x轴于点E,DF∥AC交抛物线对称轴于点F,求DE+DF的最大值;
(3)①在拋物线上是否存在点P,使以点A,P,C为顶点的三角形,是以AC为直角边的直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
②点Q在抛物线对称轴上,其纵坐标为t,请直接写出△ACQ为锐角三角形时t的取值范围.
31.如图(1),抛物线y=ax2+bx经过A和B(3,﹣3)两点,点A在x轴的正半轴,且OA=4.
(1)求抛物线的解析式;
(2)若点M是抛物线上一动点,且在直线OB的下方(不与O、B重合),过M作MK⊥x轴,交直线BO于点N,过M作MP∥x轴,交直线BO于点P,求出△MNP周长的最大值及周长取得最大值时点M的坐标;
(3)如图(2),过B作BD⊥y轴于点D,交抛物线于点C,连接OC,在抛物线上是否存在点Q使得S△OCD:S△OCQ=3:2,若存在,请求出点Q的坐标,若不存在,请说明理由.
32.已知抛物线与x轴交于点A(﹣2,0)、B(3,0),与y轴交于点C(0,4).
(1)求抛物线的解析式;
(2)如图1,点P是抛物线上位于第一象限内的一点,当四边形ABPC的面积最大时,求出四边形ABPC的面积最大值及此时点P的坐标.
(3)如图2,将抛物线向右平移个单位,再向下平移2个单位.记平移后的抛物线为y',若抛物线y'与原抛物线对称轴交于点Q.点E是新抛物线y'对称轴上一动点,在(2)的条件下,当△PQE是等腰三角形时,求点E的坐标.
答案
一.选择题
C.D.B.B.B.A.A.A.D.D.C.C.C.B.
二.填空题
15.1920.
16.﹣2.
17.10.
18.s≥9.
19.a≤3.
20.k.
21.1或4.
22.﹣16.
23.﹣8.
24.y=x2﹣4x+3.
25.a<0或0<a.
三.解答题
26.(1)设钢笔、笔记本的单价分别为x元、y元,根据题意,得,
解这个方程组,得,
所以钢笔、笔记本的单价分别为10元、6元;
(2)这次奖励一等奖的学生为a人,购买奖品总余额为w元,
则w=a[10﹣0.1(a﹣30)]+6(100﹣a)=﹣0.1a2+7a+600=﹣0.1(a﹣35)2+722.5,
∵30≤a≤50
∴a=50时w=﹣0.1×(50﹣35)2+722.5=700(元)最少,
所以这次奖励学生一等奖为50人时,购买奖品总额最少,最少为700元.
27.(1)根据题意,得:5000x2+70000x﹣225000=﹣5000(x﹣7)2+20000,
答:y与x的函数关系式为y=﹣5000x2+70000x﹣225000;
(2)由题意,得,
解得x≥7.2,
∵a=﹣5000<0,
∴抛物线开口向下,对称轴为直线x=7,
∵x≥7.2,
∴此时函数图象在对称轴的右侧,y随x的增大而减小,
∴x=7.2(元)时,y取得最大值,ymax=19800(元);
答:当批发单价为7.2元时,饮料厂每天的利润最大,最大利润是19800元;
(3)根据题意得﹣5000x2+70000x﹣225000=18750,
解得:x1=6.5,x2=7.5,
∵抛物线开口向下,
∴当6.5≤x≤7.5时,每天的利润不低于18700元,
∵每天的总成本不超过42500元,
∴,
解得x≥7.3,
∴7.3≤x≤7.5,
答:批发单价应控制在7.3元到7.5元之间.
28.(1)将点A、B的坐标代入抛物线表达式得:,
解得,
∴抛物线的解析式为:y=﹣x2+4x﹣3;
(2)如下图,连接BC交DE于点M,此时MA+MC最小,
又因为AC是定值,所以此时△AMC的周长最小.
由题意可知OB=OC=3,OA=1,
∴BC3,同理AC,
∴此时△AMC的周长=AC+AM+MC=AC+BC3;
∵DE是抛物线的对称轴,与x轴交点A(1,0)和B(3,0),
∴AE=BE=1,对称轴为 x=2,
由OB=OC,∠BOC=90°得∠OBC=45°,
∴EB=EM=1,
又∵点M在第四象限,在抛物线的对称轴上,
∴M(2,﹣1);
(3)存在这样的点P,使△FCG是等腰三角形.
∵点P的横坐标为m,故点F(m,﹣m2+4m﹣3),点G(m,m﹣3),
则FG2=(﹣m2+4m﹣3)2,CF2=(m2﹣3m)2,GC2=2m2,
当FG=FC时,则(﹣m2+4m﹣3)2=(m2﹣3m)2,解得m=0(舍去)或4;
当GF=GC时,同理可得m=0(舍去)或3;
当FC=GC时,同理可得m=0(舍去)或5,
综上,m=5或m=4或或3.
29.(1)设销量y与降价x之间的关系式y=kx+b,
将点(2,24)、(4,28)代入上式得,解得,
故销量y与降价x之间的关系式y=2x+20;
(2)由题意得:(80﹣x﹣50)(2x+20)=750,
解得x=5或15(元),
故该玩具每个降价5元或15元,可以恰好获得750元的利润;
(3)由题意得:W=(80﹣x﹣50)(2x+20)=﹣2(x﹣10)2+800,
∵﹣2<0,
故当x=10(元)时,W的最大值为800(元).
30.(1)设抛物线解析式为y=a(x+1)(x﹣3),
即y=ax2﹣2ax﹣3a,
∴﹣2a=2,解得a=﹣1,
∴抛物线解析式为y=﹣x2+2x+3;
(2)当x=0时,y=﹣x2+2x+3=3,则C(0,3),
设直线AC的解析式为y=px+q,把A(﹣1,0),
C(0,3)代入得,解得,
∴直线AC的解析式为y=3x+3,
如图1,过D作DG垂直抛物线对称轴于点G,设D(x,﹣x2+2x+3),
∵DF∥AC,
∴∠DFG=∠ACO,
而抛物线对称轴为x=1,
∴DG=x﹣1,DF(x﹣1),
∴DE+DF=﹣x2+2x+3(x﹣1)=﹣x2+(2)x+3(x)2,
∵﹣1<0,
∴当x,DE+DF有最大值为;
(3)①存在;
如图2,过点C作AC的垂线交抛物线于点P1,
∵直线AC的解析式为y=3x+3,
则直线AC倾斜角的正切值为3,则直线P1C倾斜角的正切值为,
∴直线P1C的解析式可设为yx+m,把C(0,3)代入得m=3,
∴直线P1C的解析式为yx+3,解方程组,
解得,
则此时P1点坐标为(,);
过点A作AC的垂线交抛物线于P2,
同理可设直线AP2的解析式可设为yx+n,
把A(﹣1,0)代入上式并解得n,
∴直线PC的解析式为yx,
解方程组,解得,
则此时P2点坐标为(,),
综上所述,符合条件的点P的坐标为(,)或(,);
②答:t<1或2<t.
如图3,抛物线y=﹣x2+2x+3对称轴为直线x=1,过点C作CQ1⊥AC交对称轴于Q1,过点A作AQ2⊥AC交对称轴于Q2,
∵A(﹣1,0),C(0,3),
∴直线AC解析式为y=3x+3,
∵CQ1⊥AC,
∴直线CQ1解析式为yx+3,
令x=1,得y1+3,
∴Q1(1,);
∵AQ2⊥AC,
∴直线AQ2解析式为y═x,令x=1,得y1,
∵∠AQC=90°时,AQ2+CQ2=AC2,
∴(﹣1﹣1)2+t2+(1﹣0)2+(t﹣3)2=()2,解得:t1=1,t2=2,
∴当1≤t≤2时,∠AQC≥90°,
∵△ACQ为锐角三角形,点Q(1,t)必须在线段Q1Q2上(不含端点Q1、Q2),
∴t<1或2<t.
31.(1)∵点A在x轴的正半轴,且OA=4,
∴点A(4,0),
∵抛物线y=ax2+bx经过A(4,0),B(3,﹣3),
∴,
解得,
∴抛物线解析式为:y=x2﹣4x;
(2)∵点B(3,﹣3),
∴直线OB解析式为y=﹣x,
设点M(m,m2﹣4m),
∴点N(m,﹣m),K(m,0),
∴OK=KN,
∴∠KON=∠KNO=45°,
∵MP∥x轴,
∴∠MPN=∠KON=45°,
∴∠MPN=∠KNO=∠MNP=45°,
∴MP=MN,
∴NPMN,
∵△MNP的周长=MN+MP+NP=2MNMN=2(4m﹣m2﹣m)(4m﹣m2﹣m)=(2)(3m﹣m2)=﹣(2)[(m)2],
∴当m时,△MNP的周长的最大值为,
此时点M坐标为(,);
(3)存在点Q使得S△OCD:S△OCQ=3:2,
理由如下:
如图(2),在线段CB上截取CE,连接OE,过点E作OC的平行线交抛物线于点Q,连接OQ,
∵S△OCECE×OD3=1,且OC∥QE,
∴S△OCQ=1,
∵BD⊥y轴,
∴OD=3,点C纵坐标为﹣3,
∴﹣3=x2﹣4x,
∴x1=1,x2=3,
∴点C(1,﹣3),
∴CD=1,
∴S△OCD1×3,
∴S△OCD:S△OCQ=3:2,
∵点O(0,0),点C(1,﹣3),
∴直线OC解析式为:y=﹣3x,
∵CE,
∴点E(,﹣3),
∵OC∥EQ,
∴设EQ的解析式为:y=﹣3x+b,
∴﹣3=﹣3b,
∴b=2,
∴EQ的解析式为:y=﹣3x+2,
联立方程组可得,
∴,,
∴点Q坐标为(﹣1,5)或(2,﹣4).
32.(1)∵抛物线与x轴交于点A(﹣2,0)、B(3,0),
∴可设抛物线的解析式为:y=a(x+2)(x﹣3)(a≠0),
把C(0,4)代入y=a(x+2)(x﹣3)(a≠0)中,得
4=﹣6a,
∴a,
∴抛物线的解析式为:y,
即y;
(2)设P点的坐标为(t,),过点P作PM⊥x轴,与BC交于点M,如图1,
设直线BC的解析式为y=kx+b(k≠0),则
,
解得,
∴直线BC的解析式为:y,
∴M(t,),
∴,
∴t2+3t,
,
,
∴S四边形ABPC=S△AOC+S△BOC+S△BPC,
∴当t时,S四边形ABPC取最大值,
∴此时P点的坐标为(,);
(3)∵将抛物线向右平移个单位,再向下平移2个单位.记平移后的抛物线为y',
∴y′的解析式为y,即y,
∴抛物线y′的对称轴为x=1,
∵抛物线y,
∴抛物线y的对称轴为直线x,
把x代入y中,得y=2,
∴Q点的坐标为(,2),
设E的坐标为(1,n)
①当PE=QE时,则PE2=QE2,
即,
解得,n,
∴E(1,),
②当PQ=QE时,则PQ2=QE2,
即,
解得,n=2±,
∴E点的坐标为(1,2)或(1,2);
③当PQ=PE时,则PQ2=PE2,
即,
解得,n,
∴点E的坐标为(1,)或(1,).
综上,当△PQE是等腰三角形时,点E的坐标为(1,)或(1,2)或(1,2)或(1,)或(1,).
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
