1.2.4绝对值 课件(共16张PPT)2023-2024学年人教版七年级数学上册
文档属性
| 名称 | 1.2.4绝对值 课件(共16张PPT)2023-2024学年人教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:09:43 | ||
图片预览





文档简介
(共16张PPT)
绝对值
人教版 七年级上
第一章 有理数
学习目标
学习重点:
初步了解绝对值的意义,会求一个有理数的绝对值。
01
学习难点:
有理数绝对值概念的形成及运用,理解它是“数”和“形”所结合的意义。
02
情景引入
总结反思
新知讲解
自主探索
趁热打铁
情景引入
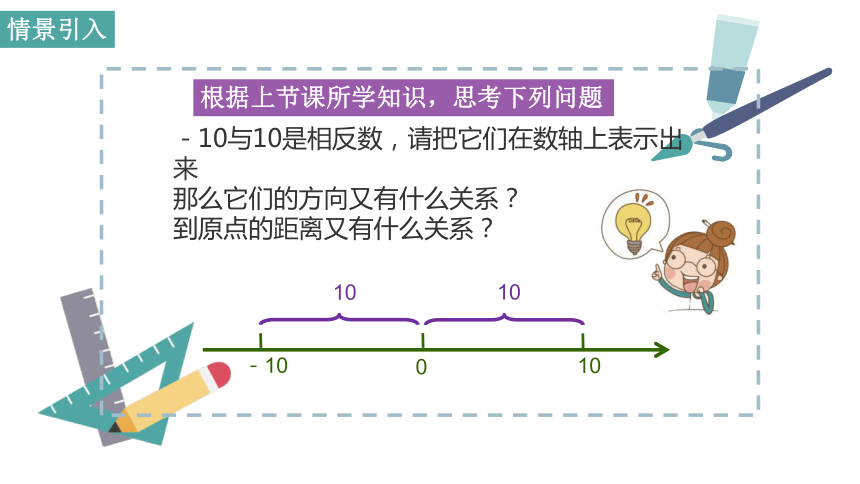
-10与10是相反数,请把它们在数轴上表示出来
那么它们的方向又有什么关系?
到原点的距离又有什么关系?
-10
10
0
10
10
根据上节课所学知识,思考下列问题
情景引入
-10与10在数轴上所表示的点到原点的距离是10个单位长度,它们的符号不同。
我们把这个距离10叫做+10和-10的绝对值。
新知讲解
绝对值的定义
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作│a│
这里的数a可以是正数、负数和0哦!
自主探索
解:根据题意可知
因为 x-4=0,y-3=0,
所以 x=4,y=3,
所以 x+y=7.
一个数的绝对值总是大于或等于0,即为非负数,若几个非负数的和为0,则这几个数都为0.
小组思考并讨论:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
|a|≥0
总结归纳:不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有
自主探索
探索小结
1.一个数的绝对值不可能为负数
2.一个正数的绝对值是它本身
3.一个负数的绝对值是它的相反数
4.零的绝对值是0
绝对值的性质
自主探索
在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
解:-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5 <-3 <0 <4
自主探索
在数轴上表示的两个数,右边的数总比左边的数大。
小 大
-5 -4 -3 -2 -1 0 1 2 3 4 5
有没有最大的有理数 有没有最小的有理数 为什么
思考:
探索小结
绝对值在数轴上
1. 表示一个数的点与原点的距离越远,这个数的绝对值越大,离原点的距离越近,这个数的绝对值越小
2.数轴上表示数的点到原点的距离只与这个点离开原点的单位长度有关,而与它所表示的数的正负性无关
3.距离不可能是负数,所以任何数的绝对值都是非负数,即│a│≥0
总结反思
绝对值
性质:
定义:
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作│a│
1.一个数的绝对值不可能为负数
2.一个正数的绝对值是它本身
3.一个负数的绝对值是它的相反数
4.零的绝对值是0
绝对值与数轴
1. 表示一个数的点与原点的距离越远,这个数的绝对值越大,离原点的距离越近,这个数的绝对值越小
2.数轴上表示数的点到原点的距离只与这个点离开原点的单位长度有关,而与它所表示的数的正负性无关
3.距离不可能是负数,所以任何数的绝对值都是非负数,即│a│≥0
趁热打铁
判断题
(1)|-1.4|>0 ( )
(2)|-0.3|=|0.3| ( )
(3)有理数的绝对值一定是正数.( )
(4)绝对值最小的数是0。( )
(5)如果数a的绝对值等于a,那么a一定为正数。( )
×
√
√
√
×
趁热打铁
(6)一个数的绝对值是4 ,则这个数是-4.( ) (7)|3|>0.( )
(8)|-1.3|>0.( )
(9)有理数的绝对值一定是正数. ( )
(10)若a=-b,则|a|=|b|. ( )
(11)若|a|=|b|,则a=b. ( )
(12)若|a|=-a,则a必为负数. ( )
(13)互为相反数的两个数的绝对值相等. ( )
√
√
√
√
×
×
×
×
趁热打铁
下列判断,正确的是( D )
A.若a>b,则│a│>│b│
B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│
D.若a>b>0,则│a│>│b│
如a=1,b=-2
如a=-3,b=2
如a=-3,b=-2
选择题
谢谢观看
绝对值
人教版 七年级上
第一章 有理数
学习目标
学习重点:
初步了解绝对值的意义,会求一个有理数的绝对值。
01
学习难点:
有理数绝对值概念的形成及运用,理解它是“数”和“形”所结合的意义。
02
情景引入
总结反思
新知讲解
自主探索
趁热打铁
情景引入
-10与10是相反数,请把它们在数轴上表示出来
那么它们的方向又有什么关系?
到原点的距离又有什么关系?
-10
10
0
10
10
根据上节课所学知识,思考下列问题
情景引入
-10与10在数轴上所表示的点到原点的距离是10个单位长度,它们的符号不同。
我们把这个距离10叫做+10和-10的绝对值。
新知讲解
绝对值的定义
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作│a│
这里的数a可以是正数、负数和0哦!
自主探索
解:根据题意可知
因为 x-4=0,y-3=0,
所以 x=4,y=3,
所以 x+y=7.
一个数的绝对值总是大于或等于0,即为非负数,若几个非负数的和为0,则这几个数都为0.
小组思考并讨论:
(1)有没有绝对值等于-2的数?
(2)一个数的绝对值会是负数吗?为什么?
(3)不论有理数a取何值,它的绝对值总是什么数?
|a|≥0
总结归纳:不论有理数a取何值,它的绝对值总是正数或0(非负数),即对任意有理数a,总有
自主探索
探索小结
1.一个数的绝对值不可能为负数
2.一个正数的绝对值是它本身
3.一个负数的绝对值是它的相反数
4.零的绝对值是0
绝对值的性质
自主探索
在数轴上表示数-3,-5,4,0,并比较它们的大小,将它们按从小到大的顺序用“<”号连接.
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
解:-3,-5,4,0在数轴上表示如图:
将它们按从小到大的顺序排列为:
-5 <-3 <0 <4
自主探索
在数轴上表示的两个数,右边的数总比左边的数大。
小 大
-5 -4 -3 -2 -1 0 1 2 3 4 5
有没有最大的有理数 有没有最小的有理数 为什么
思考:
探索小结
绝对值在数轴上
1. 表示一个数的点与原点的距离越远,这个数的绝对值越大,离原点的距离越近,这个数的绝对值越小
2.数轴上表示数的点到原点的距离只与这个点离开原点的单位长度有关,而与它所表示的数的正负性无关
3.距离不可能是负数,所以任何数的绝对值都是非负数,即│a│≥0
总结反思
绝对值
性质:
定义:
一般地,数轴上表示数a的点与原点的距离叫做数a的绝对值,记作│a│
1.一个数的绝对值不可能为负数
2.一个正数的绝对值是它本身
3.一个负数的绝对值是它的相反数
4.零的绝对值是0
绝对值与数轴
1. 表示一个数的点与原点的距离越远,这个数的绝对值越大,离原点的距离越近,这个数的绝对值越小
2.数轴上表示数的点到原点的距离只与这个点离开原点的单位长度有关,而与它所表示的数的正负性无关
3.距离不可能是负数,所以任何数的绝对值都是非负数,即│a│≥0
趁热打铁
判断题
(1)|-1.4|>0 ( )
(2)|-0.3|=|0.3| ( )
(3)有理数的绝对值一定是正数.( )
(4)绝对值最小的数是0。( )
(5)如果数a的绝对值等于a,那么a一定为正数。( )
×
√
√
√
×
趁热打铁
(6)一个数的绝对值是4 ,则这个数是-4.( ) (7)|3|>0.( )
(8)|-1.3|>0.( )
(9)有理数的绝对值一定是正数. ( )
(10)若a=-b,则|a|=|b|. ( )
(11)若|a|=|b|,则a=b. ( )
(12)若|a|=-a,则a必为负数. ( )
(13)互为相反数的两个数的绝对值相等. ( )
√
√
√
√
×
×
×
×
趁热打铁
下列判断,正确的是( D )
A.若a>b,则│a│>│b│
B.若│a│>│b│,则a>b
C.若a<b<0,则│a│<│b│
D.若a>b>0,则│a│>│b│
如a=1,b=-2
如a=-3,b=2
如a=-3,b=-2
选择题
谢谢观看
