13.3.1 等腰三角形 第1课时 课件(共15张PPT)2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 13.3.1 等腰三角形 第1课时 课件(共15张PPT)2023-2024学年人教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:16:28 | ||
图片预览




文档简介
(共15张PPT)
13.3.1 等腰三角形
第1课时
第十三章 轴对称
1.探索并证明等腰三角形的两个性质.
2.理解等腰三角形的性质并能简单应用.
观察下面的图形,它们的形状有什么特点?
它们都是等腰三角形
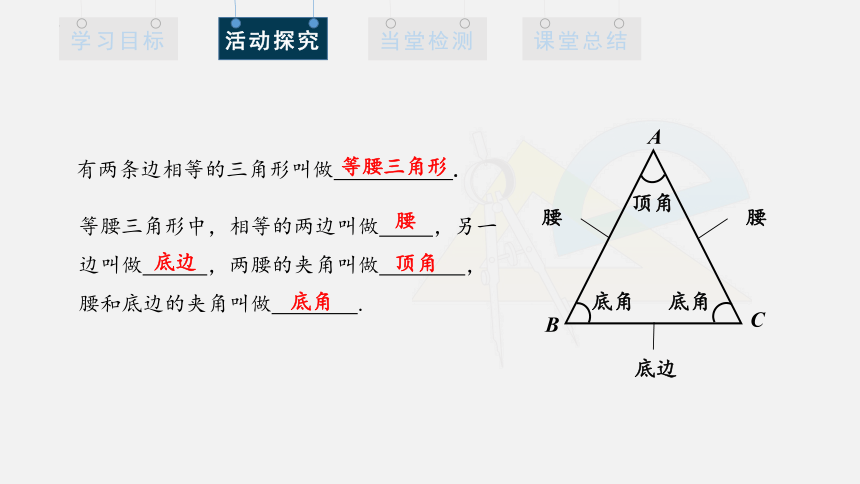
等腰三角形中,相等的两边叫做 ,另一边叫做 ,两腰的夹角叫做 ,腰和底边的夹角叫做 .
有两条边相等的三角形叫做 .
A
B
C
腰
腰
底边
底角
底角
顶角
等腰三角形
腰
底边
顶角
底角
任务一:探索并证明等腰三角形的两个性质.
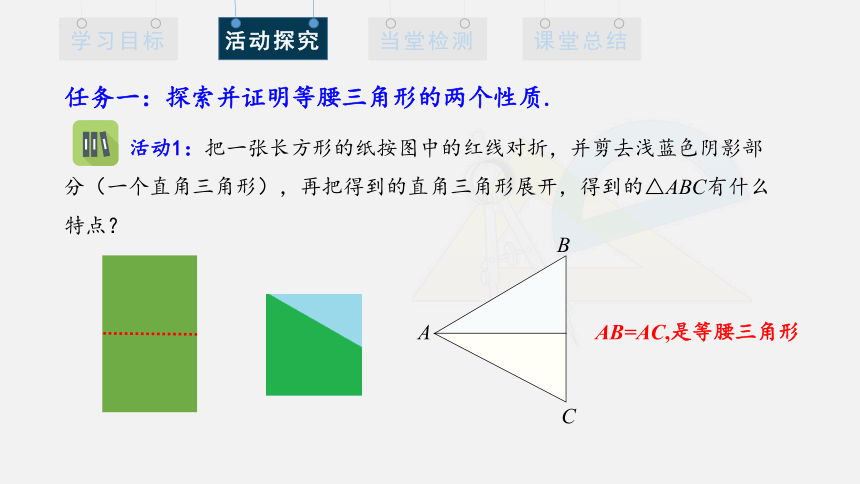
活动1:把一张长方形的纸按图中的红线对折,并剪去浅蓝色阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的△ABC有什么特点?
B
A
C
AB=AC,是等腰三角形
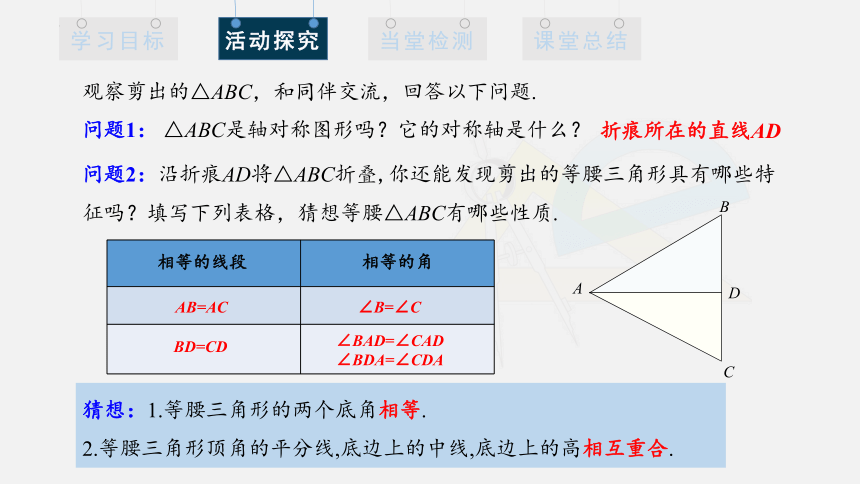
问题1: △ABC是轴对称图形吗?它的对称轴是什么?
问题2:沿折痕AD将△ABC折叠,你还能发现剪出的等腰三角形具有哪些特征吗?填写下列表格,猜想等腰△ABC有哪些性质.
B
A
C
观察剪出的△ABC,和同伴交流,回答以下问题.
D
折痕所在的直线AD
AB=AC
BD=CD
∠B=∠C
∠BAD=∠CAD
∠BDA=∠CDA
猜想:1.等腰三角形的两个底角相等.
2.等腰三角形顶角的平分线,底边上的中线,底边上的高相互重合.
相等的线段
相等的角
问题3:已知:△ABC 中,AB=AC,求证猜想.
C
A
B
D
(顶角平分线,底边上的中线、底边上的高与相互重合)
∴∠ADB=∠ADC=90°,
在Rt△ABD与Rt△ACD中,
∴Rt△ABD ≌ Rt△ACD(HL),
∴∠B=∠C,
∠CAD=∠BAD,CD=BD.
(底角相等)
证:作底边BC的高AD,交BC于点D.
活动小结
性质1:等腰三角形的两个底角相等(等边对等角).
应用格式:∵AB=AC(已知),∴∠B=∠C(等边对等角)
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(三线合一).
我们可以发现等腰三角形的性质:
练一练
如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为_______度.
34
分析:根据三角形的内角和得出
∠BAC=180°-∠B-∠C=104°,
根据等腰三角形两底角相等得出
∠BAD=∠ADB=(180°-∠B)÷2=70°,
进而根据角的和差得出∠DAC=∠BAC-∠BAD=34°.
任务二:理解等腰三角形的性质并能简单应用.
活动1:在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.和同伴交流并总结概括解题思路.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x,
在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 °,解得 x=36 ° ,
∴在△ABC中,∠A=36°,∠ABC=∠C=72°.
A
B
C
D
活动小结
利用等腰三角形等边对等角的性质:
1.先确定同一个等腰三角形中等边所对应的底角,
3.当等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小的角的度数为x.
2.利用三角形内角和的性质计算内角大小,
1.等腰三角形有一个角是90°,则另两个角分别是( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
2.如图,在△ABC中,AC=AD=DB,∠C=70°,则∠CAB的
度数为( )
A.75° B.70°
C.40° D.35°
A
A
B
D
C
3.如图,△ABC中,AB=AC,AD是BC边上的中线,CE⊥AB于点E.
求证:∠CAD=∠BCE.
证:∵AB=AC,BD=CD(已知),
∴∠B=∠ACB(等边对等角),
AD⊥BC(“三线合一”),又∵CE⊥AB(已知),
∴∠CAD+∠ACB=90°,∠BCE+∠B=90°
(直角三角形的两个锐角互余),
∴∠CAD=∠BCE(等角的余角相等).
“三线合一”
等腰三角形的两个底角相等
(“等边对等角”)
等腰三角形的性质
针对本课关键词“等腰三角形”,回答以下问题.
1.我们是怎么探究等腰三角形的性质的?
2.“三线合一”的含义是什么?请举例说明.
13.3.1 等腰三角形
第1课时
第十三章 轴对称
1.探索并证明等腰三角形的两个性质.
2.理解等腰三角形的性质并能简单应用.
观察下面的图形,它们的形状有什么特点?
它们都是等腰三角形
等腰三角形中,相等的两边叫做 ,另一边叫做 ,两腰的夹角叫做 ,腰和底边的夹角叫做 .
有两条边相等的三角形叫做 .
A
B
C
腰
腰
底边
底角
底角
顶角
等腰三角形
腰
底边
顶角
底角
任务一:探索并证明等腰三角形的两个性质.
活动1:把一张长方形的纸按图中的红线对折,并剪去浅蓝色阴影部分(一个直角三角形),再把得到的直角三角形展开,得到的△ABC有什么特点?
B
A
C
AB=AC,是等腰三角形
问题1: △ABC是轴对称图形吗?它的对称轴是什么?
问题2:沿折痕AD将△ABC折叠,你还能发现剪出的等腰三角形具有哪些特征吗?填写下列表格,猜想等腰△ABC有哪些性质.
B
A
C
观察剪出的△ABC,和同伴交流,回答以下问题.
D
折痕所在的直线AD
AB=AC
BD=CD
∠B=∠C
∠BAD=∠CAD
∠BDA=∠CDA
猜想:1.等腰三角形的两个底角相等.
2.等腰三角形顶角的平分线,底边上的中线,底边上的高相互重合.
相等的线段
相等的角
问题3:已知:△ABC 中,AB=AC,求证猜想.
C
A
B
D
(顶角平分线,底边上的中线、底边上的高与相互重合)
∴∠ADB=∠ADC=90°,
在Rt△ABD与Rt△ACD中,
∴Rt△ABD ≌ Rt△ACD(HL),
∴∠B=∠C,
∠CAD=∠BAD,CD=BD.
(底角相等)
证:作底边BC的高AD,交BC于点D.
活动小结
性质1:等腰三角形的两个底角相等(等边对等角).
应用格式:∵AB=AC(已知),∴∠B=∠C(等边对等角)
性质2:等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(三线合一).
我们可以发现等腰三角形的性质:
练一练
如图,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=40°,∠C=36°,则∠DAC的大小为_______度.
34
分析:根据三角形的内角和得出
∠BAC=180°-∠B-∠C=104°,
根据等腰三角形两底角相等得出
∠BAD=∠ADB=(180°-∠B)÷2=70°,
进而根据角的和差得出∠DAC=∠BAC-∠BAD=34°.
任务二:理解等腰三角形的性质并能简单应用.
活动1:在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.和同伴交流并总结概括解题思路.
解:∵AB=AC,BD=BC=AD,
∴∠ABC=∠C=∠BDC, ∠A=∠ABD.
设∠A=x,则∠BDC=∠A+∠ABD=2x,
从而∠ABC=∠C=∠BDC=2x,
在△ABC中,有∠A+∠ABC+∠C=x+2x+2x=180 °,解得 x=36 ° ,
∴在△ABC中,∠A=36°,∠ABC=∠C=72°.
A
B
C
D
活动小结
利用等腰三角形等边对等角的性质:
1.先确定同一个等腰三角形中等边所对应的底角,
3.当等量关系或和差关系较多时,可考虑列方程解答,设未知数时,一般设较小的角的度数为x.
2.利用三角形内角和的性质计算内角大小,
1.等腰三角形有一个角是90°,则另两个角分别是( )
A.30°,60° B.45°,45°
C.45°,90° D.20°,70°
B
2.如图,在△ABC中,AC=AD=DB,∠C=70°,则∠CAB的
度数为( )
A.75° B.70°
C.40° D.35°
A
A
B
D
C
3.如图,△ABC中,AB=AC,AD是BC边上的中线,CE⊥AB于点E.
求证:∠CAD=∠BCE.
证:∵AB=AC,BD=CD(已知),
∴∠B=∠ACB(等边对等角),
AD⊥BC(“三线合一”),又∵CE⊥AB(已知),
∴∠CAD+∠ACB=90°,∠BCE+∠B=90°
(直角三角形的两个锐角互余),
∴∠CAD=∠BCE(等角的余角相等).
“三线合一”
等腰三角形的两个底角相等
(“等边对等角”)
等腰三角形的性质
针对本课关键词“等腰三角形”,回答以下问题.
1.我们是怎么探究等腰三角形的性质的?
2.“三线合一”的含义是什么?请举例说明.
