13.3.2 等边三角形 第1课时 课件 (共16张PPT)2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 13.3.2 等边三角形 第1课时 课件 (共16张PPT)2023—2024学年人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
13.3.2 等边三角形
第1课时
第十三章 轴对称
1.会证明等边三角形的性质和判定,并能进行简单的应用.
等腰三角形
等边三角形
一般三角形
两条边相等
三条边相等
等边三角形的三条边都相等,是一种特殊的等腰三角形.
任务一:证明并掌握等边三角形的性质.
活动1:把等腰三角形的性质用于等边三角形,和同伴交流,回答以下问题.
问题1:等边三角形的三个内角之间有什么关系?
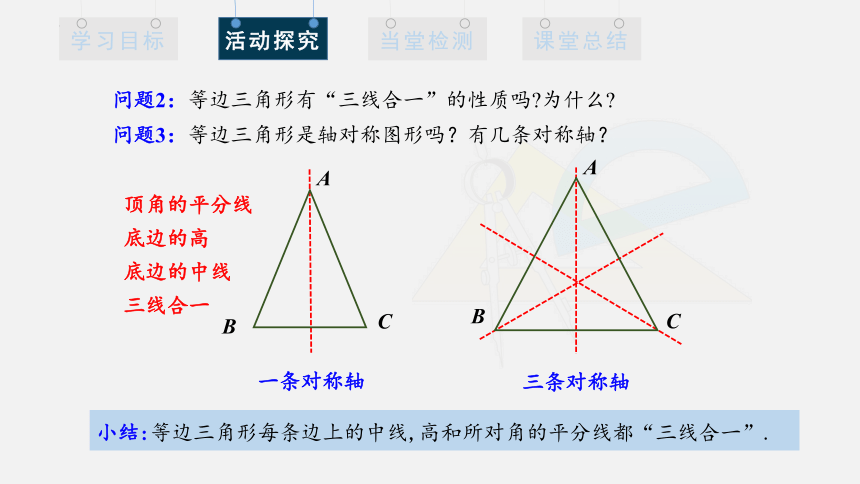
问题2:等边三角形有“三线合一”的性质吗 为什么
问题3:等边三角形是轴对称图形吗?有几条对称轴?
A
B
C
A
B
C
问题1:等边三角形的三个内角之间有什么关系?
等腰三角形:
AB=AC
∠B=∠C
等边三角形:
AC=BC,∠A=∠B
∠A=∠B=∠C
=60°
A
B
C
A
B
C
A
B
C
证明:∵AB=BC=CA,
∴∠A=∠B=∠C(等边对等角).
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
验证:如图,△ABC为等边三角形.证明∠A=∠B=∠C=60°.
结论:等边三角形的三个内角都相等,并且每一个角都等于60°.
问题2:等边三角形有“三线合一”的性质吗 为什么
A
B
C
A
B
C
顶角的平分线底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
问题3:等边三角形是轴对称图形吗?有几条对称轴?
小结:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
活动小结
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
两条边相等
三条边都相等
等腰三角形
图形
性 质
活动1:一个三角形满足什么条件就是等边三角形 和同伴交流,回答以下问题.
问题1:在△ABC中,∠A=∠B=∠C,你能得到AB=BC=CA吗?为什么?
问题2:在△ABC中,AB=BC,∠A=60°(∠B=60°或 ∠C =60°)你能得到AB=BC=CA吗?为什么?
A
B
C
任务二:证明并掌握等边三角形的判定方法.
问题1:在△ABC中,∠A=∠B=∠C,你能得到AB=BC=CA吗?为什么?
A
B
C
可以借助等腰三角形的性质来进行推导,
∠B=∠C,AB=AC( ),
同理,AC=BC,
所以 ,为等边三角形.
等角对等边
AB=AC=BC
结论:三个角都相等的三角形是等边三角形.
问题2:在△ABC中,AB=BC,∠A=60°(∠B=60°或 ∠C =60°)
你能得到AB=BC=CA吗?为什么?
在△ABC中,AB=BC,则∠A=∠C,
1.当∠A=60°时, ∠A=∠C= 60°,那么∠B= 180°-60°-60°= 60°,
∴ ∠A= ∠ B=∠C ∴ △ABC是等边三角形 ∴ AB=BC=CA
2.当∠B=60°时, 已知三角形内角和为180°,所以∠A=∠C=60°,
∴ ∠A= ∠ B=∠C ∴ △ABC是等边三角形 ∴ AB=BC=CA
结论:有一个角是60°的等腰三角形是等边三角形.
活动小结
等边三角形的判定:
判定1:三个角都相等的三角形是等边三角形.
几何语言:∵ ∠A= ∠ B=∠C
∴ AB=AC=BC(或△ABC是等边三角形)
判定2:有一个角是60°的等腰三角形是等边三角形.
几何语言:∵AB=AC ∠A= 60°∴ AB=AC=BC
练一练
如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A=∠B=∠C.
∵ DE//BC,
∴ ∠ADE=∠B, ∠AED=∠C,
∴ ∠A=∠ADE=∠AED,
∴ △ADE是等边三角形.
1.如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=( )
A.15° B.20° C.25° D.30°
A
证:∵CD∥AB,
2.如图,在△ABC中,∠B=60°,过点C作CD∥AB,若∠ACD=60°,
求证:△ABC是等边三角形.
∴∠A=∠ACD=60°,
∵∠B=60°,
在△ABC中,∠ACB=180°-∠A-∠B=60°,
∴∠A=∠B=∠ACB.
∴△ABC是等边三角形.
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰
三角形法
三条边都相等
三个角都等于60 °
有一个角是60 °
等边三角形
13.3.2 等边三角形
第1课时
第十三章 轴对称
1.会证明等边三角形的性质和判定,并能进行简单的应用.
等腰三角形
等边三角形
一般三角形
两条边相等
三条边相等
等边三角形的三条边都相等,是一种特殊的等腰三角形.
任务一:证明并掌握等边三角形的性质.
活动1:把等腰三角形的性质用于等边三角形,和同伴交流,回答以下问题.
问题1:等边三角形的三个内角之间有什么关系?
问题2:等边三角形有“三线合一”的性质吗 为什么
问题3:等边三角形是轴对称图形吗?有几条对称轴?
A
B
C
A
B
C
问题1:等边三角形的三个内角之间有什么关系?
等腰三角形:
AB=AC
∠B=∠C
等边三角形:
AC=BC,∠A=∠B
∠A=∠B=∠C
=60°
A
B
C
A
B
C
A
B
C
证明:∵AB=BC=CA,
∴∠A=∠B=∠C(等边对等角).
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
验证:如图,△ABC为等边三角形.证明∠A=∠B=∠C=60°.
结论:等边三角形的三个内角都相等,并且每一个角都等于60°.
问题2:等边三角形有“三线合一”的性质吗 为什么
A
B
C
A
B
C
顶角的平分线底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
问题3:等边三角形是轴对称图形吗?有几条对称轴?
小结:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
活动小结
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
两条边相等
三条边都相等
等腰三角形
图形
性 质
活动1:一个三角形满足什么条件就是等边三角形 和同伴交流,回答以下问题.
问题1:在△ABC中,∠A=∠B=∠C,你能得到AB=BC=CA吗?为什么?
问题2:在△ABC中,AB=BC,∠A=60°(∠B=60°或 ∠C =60°)你能得到AB=BC=CA吗?为什么?
A
B
C
任务二:证明并掌握等边三角形的判定方法.
问题1:在△ABC中,∠A=∠B=∠C,你能得到AB=BC=CA吗?为什么?
A
B
C
可以借助等腰三角形的性质来进行推导,
∠B=∠C,AB=AC( ),
同理,AC=BC,
所以 ,为等边三角形.
等角对等边
AB=AC=BC
结论:三个角都相等的三角形是等边三角形.
问题2:在△ABC中,AB=BC,∠A=60°(∠B=60°或 ∠C =60°)
你能得到AB=BC=CA吗?为什么?
在△ABC中,AB=BC,则∠A=∠C,
1.当∠A=60°时, ∠A=∠C= 60°,那么∠B= 180°-60°-60°= 60°,
∴ ∠A= ∠ B=∠C ∴ △ABC是等边三角形 ∴ AB=BC=CA
2.当∠B=60°时, 已知三角形内角和为180°,所以∠A=∠C=60°,
∴ ∠A= ∠ B=∠C ∴ △ABC是等边三角形 ∴ AB=BC=CA
结论:有一个角是60°的等腰三角形是等边三角形.
活动小结
等边三角形的判定:
判定1:三个角都相等的三角形是等边三角形.
几何语言:∵ ∠A= ∠ B=∠C
∴ AB=AC=BC(或△ABC是等边三角形)
判定2:有一个角是60°的等腰三角形是等边三角形.
几何语言:∵AB=AC ∠A= 60°∴ AB=AC=BC
练一练
如图,在等边三角形ABC中,DE∥BC, 求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A=∠B=∠C.
∵ DE//BC,
∴ ∠ADE=∠B, ∠AED=∠C,
∴ ∠A=∠ADE=∠AED,
∴ △ADE是等边三角形.
1.如图,已知△ABC是等边三角形,点B,C,D,E在同一直线上,且CG=CD,DF=DE,则∠E=( )
A.15° B.20° C.25° D.30°
A
证:∵CD∥AB,
2.如图,在△ABC中,∠B=60°,过点C作CD∥AB,若∠ACD=60°,
求证:△ABC是等边三角形.
∴∠A=∠ACD=60°,
∵∠B=60°,
在△ABC中,∠ACB=180°-∠A-∠B=60°,
∴∠A=∠B=∠ACB.
∴△ABC是等边三角形.
定义
底=腰
特殊性
性质
特殊性
边
三边相等
角
三个角都等于60 °
轴对称性
轴对称图形,每条边上都具有“三线合一”性质
判定
特殊性
三边法
三角法
等腰
三角形法
三条边都相等
三个角都等于60 °
有一个角是60 °
等边三角形
