13.1.1 轴对称 课件(共16张PPT)2022-2023学年人教版八年级数学上册
文档属性
| 名称 | 13.1.1 轴对称 课件(共16张PPT)2022-2023学年人教版八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 10:37:20 | ||
图片预览






文档简介
(共16张PPT)
第十三章 轴对称
13.1 轴对称
13.1.1 轴对称
1.了解轴对称图形和两个图形成轴对称的概念,知道它们的区别和联系.
2.探索并掌握成轴对称的两个图形的性质和轴对称图形的性质.
观察下列图片,你能发现什么共同规律吗?再想一想,在我们的生活中还有没有这样的形象呢?试举例.
任务一:了解轴对称图形和两个图形成轴对称的概念.
折线两边的图案能相互重合
轴对称图形
活动1:把一张纸对折,剪出一个图案(折痕处不完全剪断),再打开这张对折的纸.就得到了美丽的窗花.观察得到的窗花,你能发现它们有什么共同的特点吗?
小结:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
下面这些图形是轴对称图形吗?如果是,有几条对称轴?
练一练
1条
2条
4条
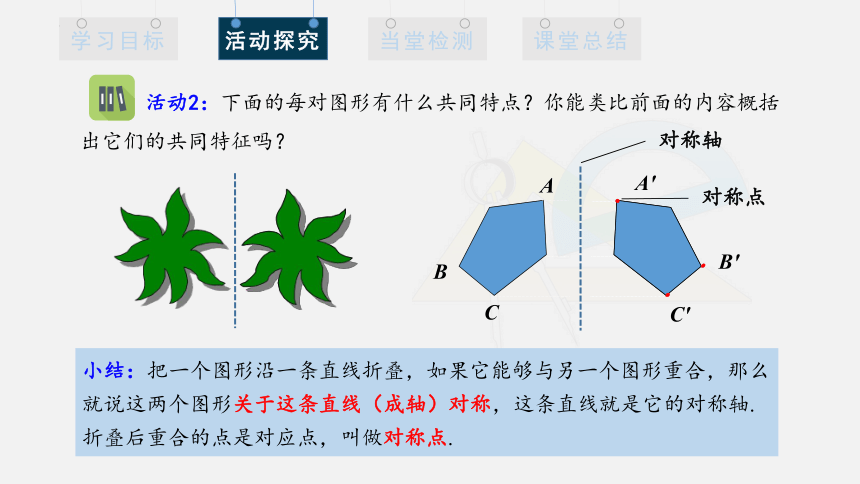
活动2:下面的每对图形有什么共同特点?你能类比前面的内容概括出它们的共同特征吗?
小结:把一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线就是它的对称轴.折叠后重合的点是对应点,叫做对称点.
A
B
C
·
A′
B′
·
C′
·
对称点
对称轴
想一想:你能说明轴对称图形和两个图形成轴对称有什么区别和联系吗?
名称 关系 轴对称 轴对称图形
区别 意义不同 两个图形之间的对称关系 具有特殊位置关系的图形
对象不同 两个图形 一个图形
对称轴的位置不同 在两个图形之间 过图形的某条直线
联系 (1)如果把成轴对称的两个图形看成一个整体,那么这个整体就是一个轴对称图形;(2)如果把一个轴对称图形位于对称轴两旁的部分看成两个图形,那么这两个图形就成轴对称
练一练
已知图中的两个三角形关于直线m对称,请说出图中的哪些点可以重合?
m
A
B
C
D
F
E
____的对称点是点E
点D
点A的对称点是点F
对称点
点B
点C的对称点是_____
能重合的点叫_________.
任务二:探索并掌握成轴对称的两个图形的性质和轴对称图形的性质.
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
活动1:如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
线段垂直平分线的定义:
经过线段中点并且垂直于这条线段的直线,
叫做这条线段的垂直平分线.
图形轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
如图,MN⊥AA′, AP=A′P. 直线MN是
线段AA ′的垂直平分线.
思考:一个轴对称图形的对称轴是否也具有上述性质呢?
轴对称图形的性质:轴对称图形的对称轴,
是任何一对对应点所连线段的垂直平分线.
如右图,MN垂直平分AA ′, MN垂直平分BB ′.
A
B
A ′
B ′
M
N
练一练
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
A
1.下列“数字”图形中,有且仅有一条对称轴的是( )
A
2.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
A.AC=A′C′ B.BO=B′O
C.AA′⊥MN D.AB∥B′C′
D
3.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
B
A.4cm2 B.8cm2
C.12cm2 D.16cm2
针对本课关键词“轴对称”,请回答以下问题.
1.轴对称图形和图形的轴对称的区别与联系是什么?
2.成轴对称的两个图形有什么性质 轴对称图形有什么性质?
第十三章 轴对称
13.1 轴对称
13.1.1 轴对称
1.了解轴对称图形和两个图形成轴对称的概念,知道它们的区别和联系.
2.探索并掌握成轴对称的两个图形的性质和轴对称图形的性质.
观察下列图片,你能发现什么共同规律吗?再想一想,在我们的生活中还有没有这样的形象呢?试举例.
任务一:了解轴对称图形和两个图形成轴对称的概念.
折线两边的图案能相互重合
轴对称图形
活动1:把一张纸对折,剪出一个图案(折痕处不完全剪断),再打开这张对折的纸.就得到了美丽的窗花.观察得到的窗花,你能发现它们有什么共同的特点吗?
小结:如果一个平面图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.
下面这些图形是轴对称图形吗?如果是,有几条对称轴?
练一练
1条
2条
4条
活动2:下面的每对图形有什么共同特点?你能类比前面的内容概括出它们的共同特征吗?
小结:把一个图形沿一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线(成轴)对称,这条直线就是它的对称轴.折叠后重合的点是对应点,叫做对称点.
A
B
C
·
A′
B′
·
C′
·
对称点
对称轴
想一想:你能说明轴对称图形和两个图形成轴对称有什么区别和联系吗?
名称 关系 轴对称 轴对称图形
区别 意义不同 两个图形之间的对称关系 具有特殊位置关系的图形
对象不同 两个图形 一个图形
对称轴的位置不同 在两个图形之间 过图形的某条直线
联系 (1)如果把成轴对称的两个图形看成一个整体,那么这个整体就是一个轴对称图形;(2)如果把一个轴对称图形位于对称轴两旁的部分看成两个图形,那么这两个图形就成轴对称
练一练
已知图中的两个三角形关于直线m对称,请说出图中的哪些点可以重合?
m
A
B
C
D
F
E
____的对称点是点E
点D
点A的对称点是点F
对称点
点B
点C的对称点是_____
能重合的点叫_________.
任务二:探索并掌握成轴对称的两个图形的性质和轴对称图形的性质.
A
B
C
A′
B′
C′
N
M
AA′⊥MN,
BB′⊥MN,
CC′⊥MN.
活动1:如图,△ABC和△A′B′C′关于直线MN对称,点A′,B′,C′分别是点A,B,C的对称点,线段AA′,BB′,CC′与直线MN有什么关系?
线段垂直平分线的定义:
经过线段中点并且垂直于这条线段的直线,
叫做这条线段的垂直平分线.
图形轴对称的性质:
如果两个图形关于某条直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.
如图,MN⊥AA′, AP=A′P. 直线MN是
线段AA ′的垂直平分线.
思考:一个轴对称图形的对称轴是否也具有上述性质呢?
轴对称图形的性质:轴对称图形的对称轴,
是任何一对对应点所连线段的垂直平分线.
如右图,MN垂直平分AA ′, MN垂直平分BB ′.
A
B
A ′
B ′
M
N
练一练
如图,一种滑翔伞的形状是左右成轴对称的四边形ABCD,其中∠BAD=150°,∠B=40°,则∠BCD的度数是( )
A.130° B.150°
C.40° D.65°
A
1.下列“数字”图形中,有且仅有一条对称轴的是( )
A
2.如图,若△ABC与△A′B′C′关于直线MN对称,BB′交MN于点O,则下列说法不一定正确的是( )
A.AC=A′C′ B.BO=B′O
C.AA′⊥MN D.AB∥B′C′
D
3.如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为( )
B
A.4cm2 B.8cm2
C.12cm2 D.16cm2
针对本课关键词“轴对称”,请回答以下问题.
1.轴对称图形和图形的轴对称的区别与联系是什么?
2.成轴对称的两个图形有什么性质 轴对称图形有什么性质?
