2023—2024学年人教版数学八年级上册14.1.4.2 多项式与多项式相乘 课件 (共15张PPT)
文档属性
| 名称 | 2023—2024学年人教版数学八年级上册14.1.4.2 多项式与多项式相乘 课件 (共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
14.1 整式的乘法
14.1.4.2 多项式乘多项式
第十四章 整式的乘法与因式分解
1.探索并了解多项式乘以多项式的运算法则;
2.能运用多项式与多项式相乘的法则进行简单的运算.
任务一:了解多项式乘以多项式的运算法则.
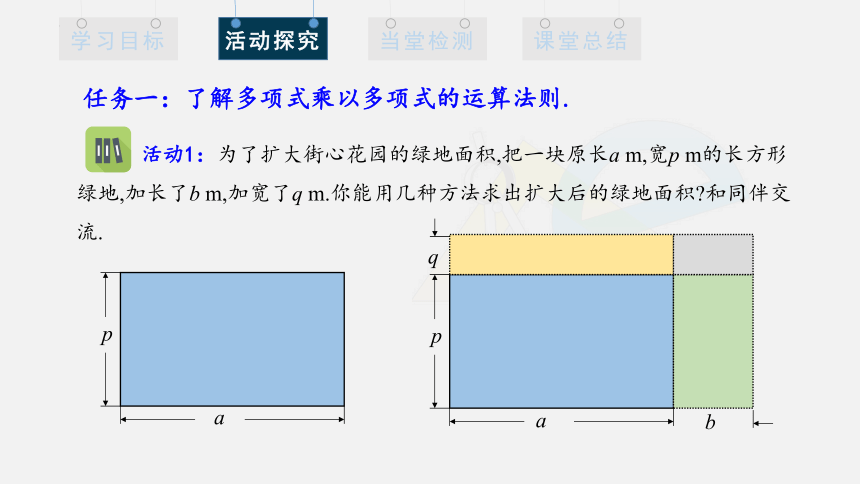
活动1:为了扩大街心花园的绿地面积,把一块原长a m,宽p m的长方形绿地,加长了b m,加宽了q m.你能用几种方法求出扩大后的绿地面积 和同伴交流.
p
a
q
b
p
a
1.可以将扩大后的绿地看成四个小的长方形.
2.可以将扩大后的绿地看成两个稍大的长方形.
3.可以将扩大后的绿地直接看成一个大的长方形.
a(p+q)+b(p+q)
p(a+b)+q(a+b)
(a+b)(p+q)
ap+aq+bp+bq
p
a
q
b
ap
bp
bp
aq
沿紫线分开:
沿红线分开:
想一想:下面四个式子都是扩大后的绿地面积,根据上节课积累的探究经验,你能得出什么结论呢?
a(p+q)+b(p+q)
p(a+b)+q(a+b)
(a+b)(p+q)
ap+aq+bp+bq
(a+b)(p+q)
a(p+q)+b(p+q)
p(a+b)+q(a+b)
ap+aq+bp+bq
多项式乘多项式
单项式乘多项式
单项式乘单项式
活动小结
多项式乘多项式的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)( p+q)=
几何语言:
ap+aq+bp+bq
活动1:如图,在某住房小区的建设中,为了提高业主的居住环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.和同伴交流,完成以下问题.
任务二:运用多项式与多项式相乘的法则进行简单的运算.
4a+3b
2a+3b
b
b
问题1:用字母a和b表示剩余草坪的面积.
问题2:有没有别的方法计算更简单呢?
问题3:当a=2,b=1时,剩余草坪的面积是多少?
问题1:用字母a和b表示剩余草坪的面积.
解:(4a+3b)(2a+3b)-b(2a+3b)-b(4a+3b)
=8a2+6ab+12ab+9b2-2ab-3b2-4ab-3b2+b2
=8a2+12ab+4b2(平方米)
4a+3b
2a+3b
b
b
4a+3b
2a+3b
b
b
问题2:有没有别的方法计算更简单呢?
(4a+3b-b)(2a+3b-b)
=(4a+2b)(2a+2b)
=8a2+12ab+4b2(平方米)
问题3:当a=2,b=1时,剩余草坪的面积是多少?
当a=2,b=1, 8a2+12ab+4b2=
8×4+12×2×1+4×1
=60(平方米)
+b2
活动2:和同伴交流,完成以下问题,说说多项式与多项式相乘应该注意什么?
( 1 ) (3x+1) (x+2)
( 3 ) (x+y)(x2 -xy+ y2).
( 2 ) (x-8y)(x - y).
解: (1) 原式=3x·x+2·3x+x+1×2
(2) 原式=x·x-xy-8xy+8y2
=3x2+7x+2;
=x2-9xy+8y2;
=3x2+6x+x+2
(3)原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
活动小结
(1)必须做到不重复,不漏乘;
(2)符号问题:确定积中每一项的符号;
(3)最后结果应化成最简形式.
多项式与多项式相乘应注意的几个问题:
练一练
已知ax2+2bx+2(a≠0)与x-1的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+2bx+2)(x-1)
=ax3-ax2+2bx2-2bx+2x-2,
∵积不含x2的项,也不含x的项,
-a+2b=0
-2b+2=0
∴
解得
a=2
b=1
1.下列多项式相乘的结果为x2 +3x﹣18的是( )
A.(x-2)(x+9) B.(x+2)(x﹣9)
C.(x+3(x﹣6) D.(x﹣3(x+6)
D
c
c
a
b
2.有一长方形耕地,其中长为a,宽为b,现要在该耕地上种植两块防风带,如图所示的绿色部分,其中横向防风带为长方形,纵向防风带为平行四边形,则剩余耕地面积为( )
B
A、bc-ab+ac+c2 B、ab-bc-ac+c2
C、a2+ab+bc-ac D、b2-bc+a2-ab
3.化简求值:(2x+5y)(2x-5y) -(x+5y)(4x-5y),其中x=3,y=-1.
解:(2x+5y)(2x-5y) -(x+5y)(4x-5y)
=4x2-10xy+10xy-25y2-(4x2-5xy+20xy-25y2)
=4x2-10xy+10xy-25y2-4x2+5xy - 20xy+25y2)
=- 15xy
当x=3,y=-1时,原式=-15 ×3 ×(-1)=45
多项式乘多项式
运算法则
注意事项
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(1)不要漏乘;
(2)正确确认各部分的符号;
(3)结果需要化为最简形式.
实质上是转化为单项式乘单项式
14.1 整式的乘法
14.1.4.2 多项式乘多项式
第十四章 整式的乘法与因式分解
1.探索并了解多项式乘以多项式的运算法则;
2.能运用多项式与多项式相乘的法则进行简单的运算.
任务一:了解多项式乘以多项式的运算法则.
活动1:为了扩大街心花园的绿地面积,把一块原长a m,宽p m的长方形绿地,加长了b m,加宽了q m.你能用几种方法求出扩大后的绿地面积 和同伴交流.
p
a
q
b
p
a
1.可以将扩大后的绿地看成四个小的长方形.
2.可以将扩大后的绿地看成两个稍大的长方形.
3.可以将扩大后的绿地直接看成一个大的长方形.
a(p+q)+b(p+q)
p(a+b)+q(a+b)
(a+b)(p+q)
ap+aq+bp+bq
p
a
q
b
ap
bp
bp
aq
沿紫线分开:
沿红线分开:
想一想:下面四个式子都是扩大后的绿地面积,根据上节课积累的探究经验,你能得出什么结论呢?
a(p+q)+b(p+q)
p(a+b)+q(a+b)
(a+b)(p+q)
ap+aq+bp+bq
(a+b)(p+q)
a(p+q)+b(p+q)
p(a+b)+q(a+b)
ap+aq+bp+bq
多项式乘多项式
单项式乘多项式
单项式乘单项式
活动小结
多项式乘多项式的法则:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.
(a+b)( p+q)=
几何语言:
ap+aq+bp+bq
活动1:如图,在某住房小区的建设中,为了提高业主的居住环境,小区准备在一个长为(4a+3b)米,宽为(2a+3b)米的长方形草坪上修建两条宽为b米的通道.和同伴交流,完成以下问题.
任务二:运用多项式与多项式相乘的法则进行简单的运算.
4a+3b
2a+3b
b
b
问题1:用字母a和b表示剩余草坪的面积.
问题2:有没有别的方法计算更简单呢?
问题3:当a=2,b=1时,剩余草坪的面积是多少?
问题1:用字母a和b表示剩余草坪的面积.
解:(4a+3b)(2a+3b)-b(2a+3b)-b(4a+3b)
=8a2+6ab+12ab+9b2-2ab-3b2-4ab-3b2+b2
=8a2+12ab+4b2(平方米)
4a+3b
2a+3b
b
b
4a+3b
2a+3b
b
b
问题2:有没有别的方法计算更简单呢?
(4a+3b-b)(2a+3b-b)
=(4a+2b)(2a+2b)
=8a2+12ab+4b2(平方米)
问题3:当a=2,b=1时,剩余草坪的面积是多少?
当a=2,b=1, 8a2+12ab+4b2=
8×4+12×2×1+4×1
=60(平方米)
+b2
活动2:和同伴交流,完成以下问题,说说多项式与多项式相乘应该注意什么?
( 1 ) (3x+1) (x+2)
( 3 ) (x+y)(x2 -xy+ y2).
( 2 ) (x-8y)(x - y).
解: (1) 原式=3x·x+2·3x+x+1×2
(2) 原式=x·x-xy-8xy+8y2
=3x2+7x+2;
=x2-9xy+8y2;
=3x2+6x+x+2
(3)原式=x·x2-x·xy+xy2+x2y-xy2+y·y2
=x3-x2y+xy2+x2y-xy2+y3
= x3+y3.
活动小结
(1)必须做到不重复,不漏乘;
(2)符号问题:确定积中每一项的符号;
(3)最后结果应化成最简形式.
多项式与多项式相乘应注意的几个问题:
练一练
已知ax2+2bx+2(a≠0)与x-1的积不含x2项,也不含x项,求系数a、b的值.
解:(ax2+2bx+2)(x-1)
=ax3-ax2+2bx2-2bx+2x-2,
∵积不含x2的项,也不含x的项,
-a+2b=0
-2b+2=0
∴
解得
a=2
b=1
1.下列多项式相乘的结果为x2 +3x﹣18的是( )
A.(x-2)(x+9) B.(x+2)(x﹣9)
C.(x+3(x﹣6) D.(x﹣3(x+6)
D
c
c
a
b
2.有一长方形耕地,其中长为a,宽为b,现要在该耕地上种植两块防风带,如图所示的绿色部分,其中横向防风带为长方形,纵向防风带为平行四边形,则剩余耕地面积为( )
B
A、bc-ab+ac+c2 B、ab-bc-ac+c2
C、a2+ab+bc-ac D、b2-bc+a2-ab
3.化简求值:(2x+5y)(2x-5y) -(x+5y)(4x-5y),其中x=3,y=-1.
解:(2x+5y)(2x-5y) -(x+5y)(4x-5y)
=4x2-10xy+10xy-25y2-(4x2-5xy+20xy-25y2)
=4x2-10xy+10xy-25y2-4x2+5xy - 20xy+25y2)
=- 15xy
当x=3,y=-1时,原式=-15 ×3 ×(-1)=45
多项式乘多项式
运算法则
注意事项
多项式与多项式相乘,先用一个多项式的每一项分别乘以另一个多项式的每一项,再把所得的积相加.
(1)不要漏乘;
(2)正确确认各部分的符号;
(3)结果需要化为最简形式.
实质上是转化为单项式乘单项式
