2023-2024学年人教版八年级上册数学第十三章 轴对称 复习课(共28张PPT)
文档属性
| 名称 | 2023-2024学年人教版八年级上册数学第十三章 轴对称 复习课(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 971.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览








文档简介
(共28张PPT)
八年级·数学·人教版·上册
第十三章 复习课
第十三章 复习课
1.能说出轴对称图形、轴对称的概念及性质.
2.能按要求作出简单平面图形经过一次或两次轴对称后的图形,能指出对称轴.
3.能用尺规作图作出线段的垂直平分线,能利用垂直平分线的性质解决问题.
4.能说出等腰(等边)三角形的性质和判定,并能熟练应用,解决问题.
◎重点:轴对称的性质、等腰三角形的性质和判定.
◎难点:轴对称的性质、等腰三角形的性质和判定的应用.
这一章我们重点学习了轴对称和等腰三角形的知识,你能将本章所学的定义、定理完整地叙述出来吗 你能将本章的知识梳理成一个知识结构图吗
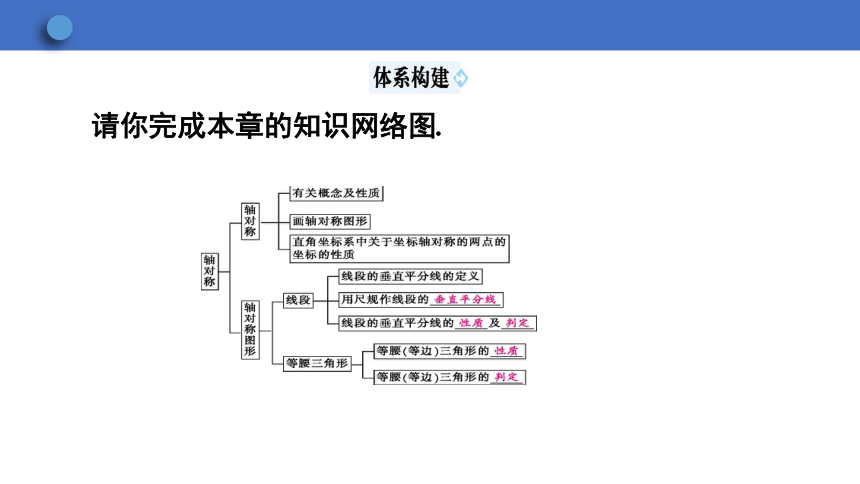
请你完成本章的知识网络图.
·导学建议·
每章学完后,可以让学生自己画知识网络图,对系统掌握一章的知识有很大的好处.
1. 叫做线段的垂直平分线.
2.轴对称图形的对称轴,是
.
3.线段垂直平分线的性质是
.
经过线段中点并且垂直于这条线段的直线
任何一对对应点所连线段的垂直平分线
线段垂直平分线上的点与这条线段两个端点的距离相等
4.点(x,y)关于x轴对称的点的坐标为 ,关于y轴对称的点的坐标为 .
5.等腰三角形两个底角 .(简称: )
6.等腰三角形的 、 、
互相重合.
7.一个三角形有两个角相等,这两个角所对的边也
.(简称: )
等角对等边
(x,-y)
(-x,y)
相等
等边对等角
等边对等角
底边上的中线
底边上的高
相等
8.三个角 的三角形是等边三角形.
9.有一个角是 的等腰三角形是等边三角形.
10.直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的 .
一半
都相等
60°
·导学建议·
预习导学部分可由教师提问学生回答的形式完成,建议学生在课前对不熟悉的知识自己复习.
轴对称图形(图案)的识别问题
1.下列图案是轴对称图形的有 ( )
A.1个 B.2个 C.3个 D.4个
B
判断一个图形是不是轴对称图形,关键是看图形沿某条直线折叠后,直线两旁的部分能不能 .
完全重合
·导学建议·
轴对称图形的判断最常见的判断方法是从纸的背面看图形,如果看到的图形与原图形一样,则该图形是轴对称图形,要通过实践让学生掌握这种判断方法.
画轴对称图形
2.如图,在直角坐标系中,A(-1,5),B(-3,0),C(-4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)写出点C1的坐标.
(3)求△ABC的面积.
解:(1)如图,△A1B1C1即为所求.
(2)点C1的坐标为(4,3).
(3)△ABC的面积=3×5-×3×1-×3×2-×5×2=.
方法归纳交流 作一个图形关于某直线对称的图形的步骤:(1)确定原图形的关键点;(2)画出关键点关于直线的
;(3)连接作出的 ,所得图形即为所作图形.
对称点
对称点
·导学建议·
轴对称图形的画法,可不要求学生能说出画法,只要能准确作出图形即可.
有关线段垂直平分线的问题
3.如图,在△ABC中,∠C=90°,DE垂直平分AB,∠CBD=∠A+15°,BC=8,AC=15,求△BCD的周长和∠ABC的度数.
解:∵DE垂直平分AB,
∴AD=BD,∴∠A=∠ABD.
∵∠CBD=∠A+15°,
∠C=90°,
∴∠A+∠A+∠A+15°=90°,
∴∠A=25°,
∴∠ABC=∠ABD+∠CBD=∠A+∠A+15°=65°.
∵AD=BD,∴CD+DB=AC=15,
∴△BCD的周长=BC+CD+BD=BC+AC=8+15=23.
方法归纳交流 在解决与线段垂直平分线有关的问题时,常把问题转化为 的问题来解决.
等腰三角形
·导学建议·
提醒学生注意,已知条件中有线段垂直平分线的,可以直接利用线段垂直平分线的性质求解,也可以转化为在等腰三角形中解决.
等腰三角形的性质和判定
4.如图,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°.
(1)求∠DAC的度数.
(2)证明:△ACD是等腰三角形.
解:(1)∵AB=AC,∠B=30°,
∴∠C=∠B=30°,
∴∠BAC=180°-∠B-∠C=120°.
∵∠DAB=45°,
∴∠DAC=∠BAC-∠DAB=120°-45°=75°.
(2)证明:∵∠DAC=75°,∠C=30°,
∴∠ADC=180°-∠C-∠DAC=75°,
∴∠DAC=∠ADC,∴AC=CD,
∴△ACD是等腰三角形.
方法归纳交流 等腰三角形的性质和判定是用来证明
、 的重要工具,但要注意等边对等角和等角对等边都是对同一个三角形而言的.
角相等
线段相等
等边三角形的性质和判定
5.如图,在等边△ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数.
(2)若CD=3,求DF的长.
解:(1)∵△ABC是等边三角形,∴∠B=60°.
∵DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°,
∴∠F=90°-∠EDC=30°.
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形,∴ED=DC=3.
∵∠DEF=90°,∠F=30°,
∴DF=2DE=6.
方法归纳交流 证明一个三角形是等边三角形的思路有哪些
答:①证明三个内角相等;②证明三边相等;③证明等腰三角形有一个内角为60°.
八年级·数学·人教版·上册
第十三章 复习课
第十三章 复习课
1.能说出轴对称图形、轴对称的概念及性质.
2.能按要求作出简单平面图形经过一次或两次轴对称后的图形,能指出对称轴.
3.能用尺规作图作出线段的垂直平分线,能利用垂直平分线的性质解决问题.
4.能说出等腰(等边)三角形的性质和判定,并能熟练应用,解决问题.
◎重点:轴对称的性质、等腰三角形的性质和判定.
◎难点:轴对称的性质、等腰三角形的性质和判定的应用.
这一章我们重点学习了轴对称和等腰三角形的知识,你能将本章所学的定义、定理完整地叙述出来吗 你能将本章的知识梳理成一个知识结构图吗
请你完成本章的知识网络图.
·导学建议·
每章学完后,可以让学生自己画知识网络图,对系统掌握一章的知识有很大的好处.
1. 叫做线段的垂直平分线.
2.轴对称图形的对称轴,是
.
3.线段垂直平分线的性质是
.
经过线段中点并且垂直于这条线段的直线
任何一对对应点所连线段的垂直平分线
线段垂直平分线上的点与这条线段两个端点的距离相等
4.点(x,y)关于x轴对称的点的坐标为 ,关于y轴对称的点的坐标为 .
5.等腰三角形两个底角 .(简称: )
6.等腰三角形的 、 、
互相重合.
7.一个三角形有两个角相等,这两个角所对的边也
.(简称: )
等角对等边
(x,-y)
(-x,y)
相等
等边对等角
等边对等角
底边上的中线
底边上的高
相等
8.三个角 的三角形是等边三角形.
9.有一个角是 的等腰三角形是等边三角形.
10.直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的 .
一半
都相等
60°
·导学建议·
预习导学部分可由教师提问学生回答的形式完成,建议学生在课前对不熟悉的知识自己复习.
轴对称图形(图案)的识别问题
1.下列图案是轴对称图形的有 ( )
A.1个 B.2个 C.3个 D.4个
B
判断一个图形是不是轴对称图形,关键是看图形沿某条直线折叠后,直线两旁的部分能不能 .
完全重合
·导学建议·
轴对称图形的判断最常见的判断方法是从纸的背面看图形,如果看到的图形与原图形一样,则该图形是轴对称图形,要通过实践让学生掌握这种判断方法.
画轴对称图形
2.如图,在直角坐标系中,A(-1,5),B(-3,0),C(-4,3).
(1)在图中作出△ABC关于y轴对称的图形△A1B1C1.
(2)写出点C1的坐标.
(3)求△ABC的面积.
解:(1)如图,△A1B1C1即为所求.
(2)点C1的坐标为(4,3).
(3)△ABC的面积=3×5-×3×1-×3×2-×5×2=.
方法归纳交流 作一个图形关于某直线对称的图形的步骤:(1)确定原图形的关键点;(2)画出关键点关于直线的
;(3)连接作出的 ,所得图形即为所作图形.
对称点
对称点
·导学建议·
轴对称图形的画法,可不要求学生能说出画法,只要能准确作出图形即可.
有关线段垂直平分线的问题
3.如图,在△ABC中,∠C=90°,DE垂直平分AB,∠CBD=∠A+15°,BC=8,AC=15,求△BCD的周长和∠ABC的度数.
解:∵DE垂直平分AB,
∴AD=BD,∴∠A=∠ABD.
∵∠CBD=∠A+15°,
∠C=90°,
∴∠A+∠A+∠A+15°=90°,
∴∠A=25°,
∴∠ABC=∠ABD+∠CBD=∠A+∠A+15°=65°.
∵AD=BD,∴CD+DB=AC=15,
∴△BCD的周长=BC+CD+BD=BC+AC=8+15=23.
方法归纳交流 在解决与线段垂直平分线有关的问题时,常把问题转化为 的问题来解决.
等腰三角形
·导学建议·
提醒学生注意,已知条件中有线段垂直平分线的,可以直接利用线段垂直平分线的性质求解,也可以转化为在等腰三角形中解决.
等腰三角形的性质和判定
4.如图,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°.
(1)求∠DAC的度数.
(2)证明:△ACD是等腰三角形.
解:(1)∵AB=AC,∠B=30°,
∴∠C=∠B=30°,
∴∠BAC=180°-∠B-∠C=120°.
∵∠DAB=45°,
∴∠DAC=∠BAC-∠DAB=120°-45°=75°.
(2)证明:∵∠DAC=75°,∠C=30°,
∴∠ADC=180°-∠C-∠DAC=75°,
∴∠DAC=∠ADC,∴AC=CD,
∴△ACD是等腰三角形.
方法归纳交流 等腰三角形的性质和判定是用来证明
、 的重要工具,但要注意等边对等角和等角对等边都是对同一个三角形而言的.
角相等
线段相等
等边三角形的性质和判定
5.如图,在等边△ABC中,点D、E分别在边BC、AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数.
(2)若CD=3,求DF的长.
解:(1)∵△ABC是等边三角形,∴∠B=60°.
∵DE∥AB,∴∠EDC=∠B=60°.
∵EF⊥DE,∴∠DEF=90°,
∴∠F=90°-∠EDC=30°.
(2)∵∠ACB=60°,∠EDC=60°,
∴△EDC是等边三角形,∴ED=DC=3.
∵∠DEF=90°,∠F=30°,
∴DF=2DE=6.
方法归纳交流 证明一个三角形是等边三角形的思路有哪些
答:①证明三个内角相等;②证明三边相等;③证明等腰三角形有一个内角为60°.
