2023-2024学年华东师大版数学九年级下册27.2.3 切线 课件(共49张PPT)
文档属性
| 名称 | 2023-2024学年华东师大版数学九年级下册27.2.3 切线 课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览





文档简介
(共49张PPT)
27.2 与圆有关的位置关系
第27章 圆
27.2.3 切线
逐点
学练
本节小结
作业提升
本节要点
1
学习流程
2
切线的判定定理
切线的性质定理
切线长定理
三角形的内切圆
知识点
切线的判定定理
1
1. 判定定理:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
特别解读
切线必须同时具备两个条件:
1.直线过半径的外端;
2.直线垂直于这条半径.
2. 切线的判定方法:
(1)定义法:与圆有唯一公共点的直线是圆的切线;
(2)数量法:与圆心的距离等于半径的直线是圆的切线;
(3)判定定理法:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
例 1
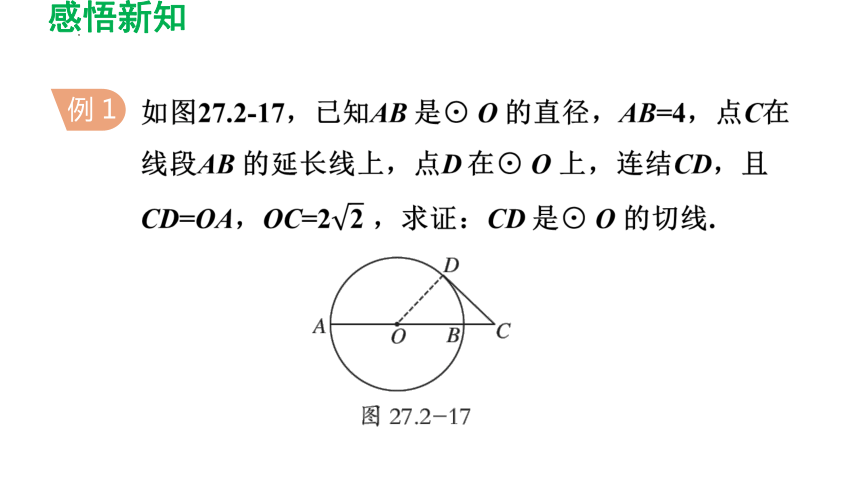
如图27.2-17,已知AB 是⊙ O 的直径,AB=4,点C在线段AB 的延长线上,点D 在⊙ O 上,连结CD,且CD=OA,OC=2 ,求证:CD 是⊙ O 的切线.
解题秘方:利用“有切点,连半径,证垂直”判定圆的切线.
证明:如图27.2-17,连结OD.
由题意可知CD=OD=OA= AB=2.
∵ OC=2,∴ OD2+CD2=OC2.
∴∠ ODC=90°,即OD ⊥ CD.
又∵点D 在⊙ O 上,∴ CD 是⊙ O 的切线.
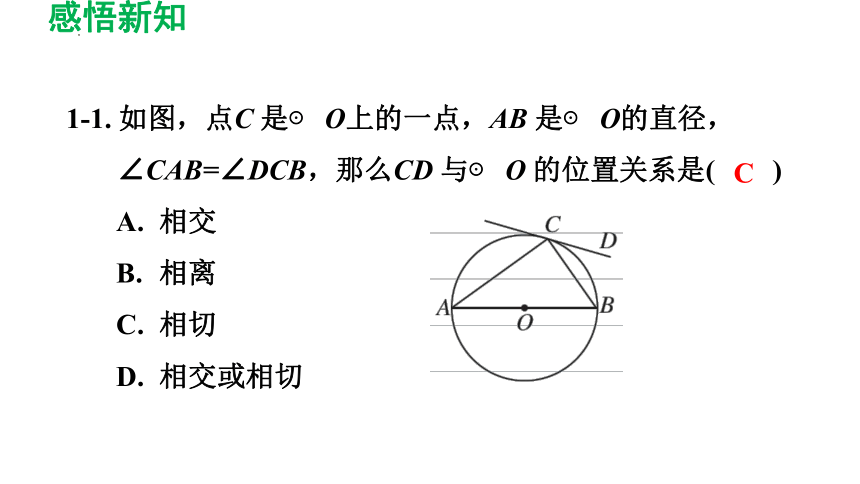
1-1. 如图,点C 是⊙ O上的一点,AB 是⊙ O的直径,∠CAB=∠DCB,那么CD 与⊙ O 的位置关系是( )
相交
相离
相切
相交或相切
C
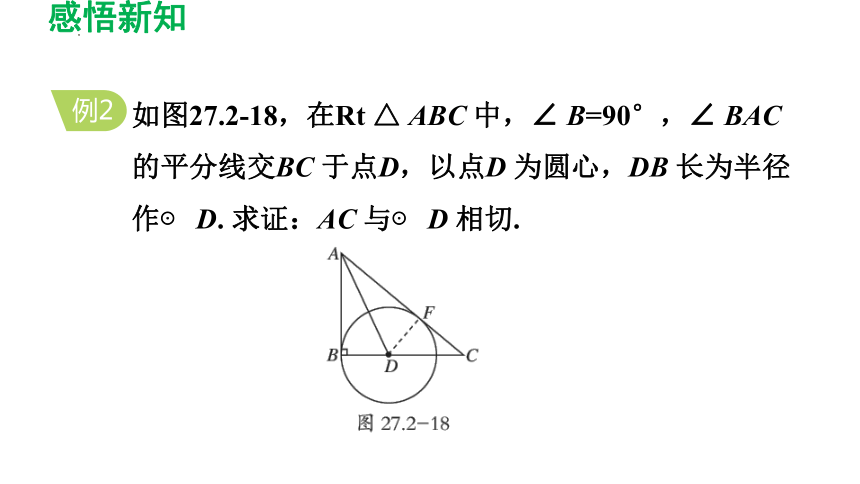
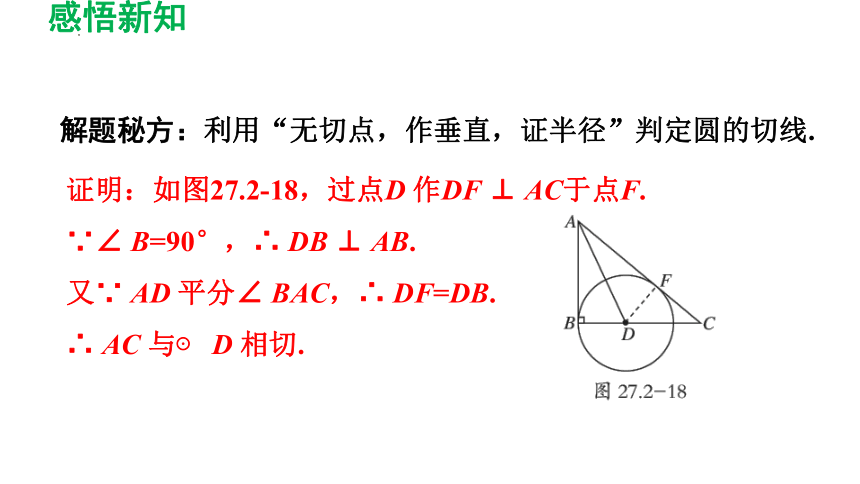
如图27.2-18,在Rt △ ABC 中,∠ B=90°,∠ BAC
的平分线交BC 于点D,以点D 为圆心,DB 长为半径作⊙ D. 求证:AC 与⊙ D 相切.
例2
解题秘方:利用“无切点,作垂直,证半径”判定圆的切线.
证明:如图27.2-18,过点D 作DF ⊥ AC于点F.
∵∠ B=90°,∴ DB ⊥ AB.
又∵ AD 平分∠ BAC,∴ DF=DB.
∴ AC 与⊙ D 相切.
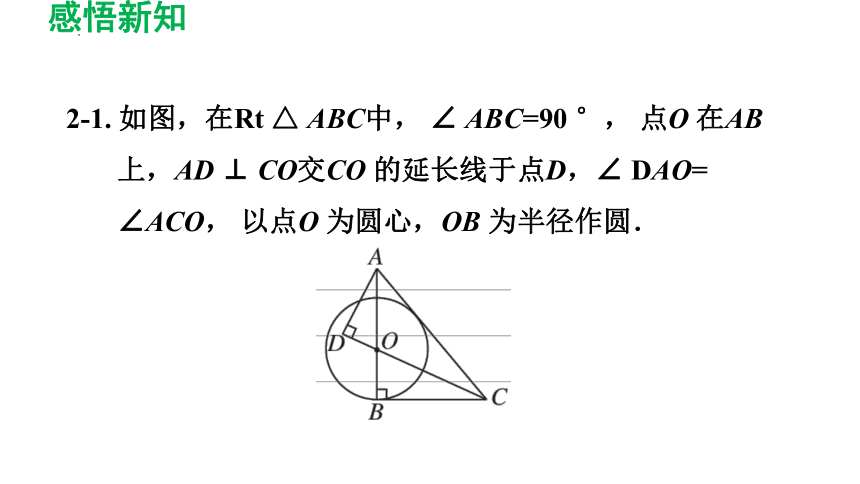
2-1. 如图,在Rt △ ABC中, ∠ ABC=90 °, 点O 在AB 上,AD ⊥ CO交CO 的延长线于点D,∠ DAO= ∠ACO, 以点O 为圆心,OB 为半径作圆.
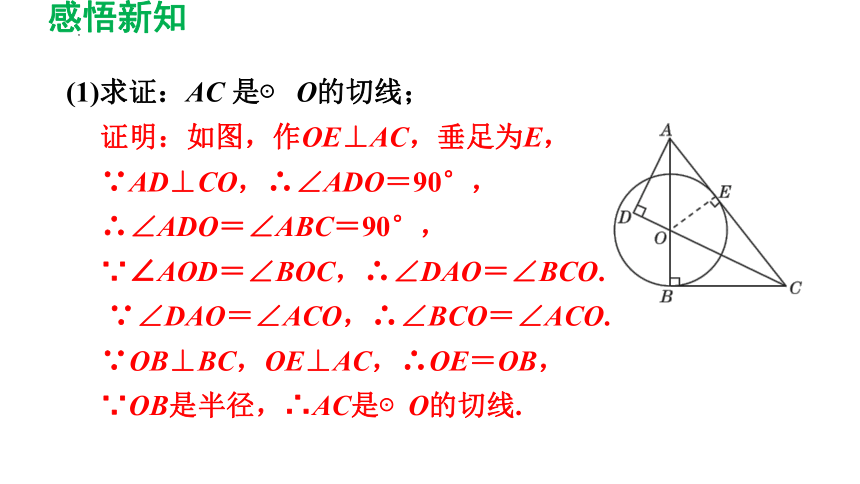
(1)求证:AC 是⊙ O的切线;
证明:如图,作OE⊥AC,垂足为E,
∵AD⊥CO,∴∠ADO=90°,
∴∠ADO=∠ABC=90°,
∵∠AOD=∠BOC,∴∠DAO=∠BCO.
∵∠DAO=∠ACO,∴∠BCO=∠ACO.
∵OB⊥BC,OE⊥AC,∴OE=OB,
∵OB是半径,∴AC是⊙O的切线.
(2)已知CB=6,AB=8,求OC 的长.
解:∵∠OBC=∠OEC,∠BCO=∠ACO,OC=OC,
∴△OBC≌△OEC,∴BC=EC=6.
知识点
切线的性质定理
2
1. 性质定理 圆的切线垂直于经过切点的半径.
2. 切线的性质 (1)切线和圆只有一个公共点.
(2)圆心到切线的距离等于半径.
(3)圆的切线垂直于过切点的半径.
(4)经过圆心且垂直于切线的直线必过切点(找切点用).
(5)经过切点且垂直于切线的直线必过圆心(找圆心用).
特别提醒
切线的判定定理与性质定理的区别:切线的判定定理是在未知相切而要证明相切的情况下使用;切线的性质定理是在已知相切而要推得其他的结论时使用.它们是一个互逆的过程,不要混淆.
如图27.2-19,AB 为⊙ O 的直径,PD 切⊙ O 于点C,交AB 的延长线于点D,且∠ D=2 ∠ CAD.
例 3
(1)求∠ D 的度数.
解题秘方:利用“等半径”得等腰三角形。
解:如图27.2-19,连结OC.
∵ AO=CO,∴∠ OAC= ∠ ACO.
∴∠ COD=2 ∠ CAD.
又∵∠ D=2 ∠ CAD,∴∠ D= ∠ COD.
∵ PD 切⊙ O 于点C,
∴ OC ⊥ PD,即∠ OCD=90° . ∴∠ D=45° .
(2)若CD=2,求BD 的长.
解:由(1)可知△ OCD 是等腰直角三角形.
∴ OC=CD=2.
由勾股定理,得OD= = =2,
∴ BD=OD-OB=2-2.
解题秘方:利用“切线垂直于过切点的半径”构造直角三角形,再结合相关性质求解.
3-1. [中考· 泰安] 如图, 在△ ABC 中,∠ B=90 °, ⊙ O 过点A,C, 与AB 交于点D,与BC 相切于点C, 若∠A=32 °, 则∠ ADO=_______.
64°
如图27.2-20,已知BC 是⊙ O 的直径,AC 切⊙O于点C,AB 交⊙ O 于点D,E 为AC 的中点,连结DE.
例4
(1)若AD=DB,OC=5,求切线AC 的长;
解题秘方:构造直径所对的圆周角,利用直径所对的圆周角是直角求解;
解:连结CD,如图27.2-20.
∵ BC 是⊙ O 的直径,
∴∠ BDC=90°,即CD ⊥ AB.
∵ AD=DB,∴ AC=BC=2OC=10.
(2)求证:DE 是⊙ O 的切线.
解题秘方:利用“连半径,证垂直”求解.
证明:连结OD,如图27.2-20.
∵∠ ADC=90°,E 为AC 的中点,
∴ DE=EC= AC. ∴∠ 1 =∠ 2.
∵ OD=OC,∴∠ 3 =∠ 4.
∵ AC 切⊙ O 于点C,∴ AC ⊥ OC.
∴∠ 1+ ∠ 3= ∠ 2+ ∠ 4 = 90°,即DE ⊥ OD.
又∵ OD 是⊙ O 的半径,∴ DE 是⊙ O 的切线.
4-1. [中考·十堰] 如图,在△ ABC 中,AB=AC,D 为AC 上一点,以CD 为直径的⊙ O 与AB 相切于点E,交BC于点F,FG ⊥ AB,垂足为G.
(1)求证:FG 是⊙ O的切线;
证明:如图,连结OF.
∵AB=AC,∴∠B=∠C,∵OF=OC,
∴∠C=∠OFC,
∴∠OFC=∠B,∴OF∥AB.
∵FG⊥AB,∴FG⊥OF.
又∵OF是⊙O的半径,∴FG是⊙O的切线.
(2)若BG=1,BF=3,求CF 的长.
解:如图,连结OE,过点O作OH⊥CF于点H.
知识点
切线长定理
3
1. 切线长定义:我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长.
切线是直线,不可度量;切线长是切线上切点与切点外另一点之间的线段的长,可以度量.
2. 切线长定理:
过圆外一点所画的圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角.
特别解读
经过圆上一点作圆的切线,有且只有一条,过切点的半径垂直于这条切线;经过圆外一点作圆的切线,有两条,这点和两个切点之间的两条线段长相等.
3. 示例:如图27.2-21 是切线长定理的一个基本图形, 可以直接得到结论:(1)PO ⊥ AB;
(2)AO ⊥ AP,BO ⊥ BP;
(3)AP=BP;
(4)∠ 1= ∠ 2= ∠ 3= ∠ 4;
(5)AD=BD;
(6)AC = BC等.
︵
︵
如图27.2-22,PA,PB,DE 分别切⊙ O 于点A,B,C,点D 在PA 上,点E 在PB 上.
例 5
解题秘方:紧扣切线长定理,切线的性质定理,四边形的内角和及角平分线的判定定理求解.
解:∵ PA,PB,DE 分别切⊙ O 于点A,B,C,
∴ PB=PA=10,DA=DC,EC=EB.
∴ PD+DE+PE=PD+DC+CE+PE=PD+DA+EB+PE=PA+
PB=10+10=20.
∴△ PDE 的周长为20.
(1)若PA=10,求△ PDE 的周长;
解:如图27.2-22,连结OA,OC,OB.
∵ PA,PB,DE 是⊙ O 的切线,
∴ OA ⊥ PA,OB ⊥ PB,OC ⊥ DE.
∴∠ DAO= ∠ EBO=90°.∴∠ P+ ∠ AOB=180°.
∴∠ AOB=180°-50°=130°.
易知∠ AOD= ∠ DOC,∠ COE= ∠ BOE,
∴∠ DOE=∠ AOB=×130°=65°.
(2)若∠ P=50°,求∠ DOE 的度数.
5-1. (易错题) 如图,直线AB,AD 分别与⊙ O 相切于点B,D,C 为⊙ O 上一点, 且∠ BCD=130°,则∠ A的度数是( )
70°
85°
80°
100°
C
5-2. 如图,PA,PB切⊙ O 于A,B 两点,CD 切⊙ O 于点E,交PA,PB 于点C,D. 若⊙ O 的半径为2,△ PCD 的周长等于4 ,则线段AB 的长是________.
知识点
三角形的内切圆
4
1. 三角形的内切圆 与三角形各边都相切的圆叫做这个三角形的内切圆,这个三角形叫做这个圆的外切三角形.
要点解读
1. 一个三角形有一个内切圆,而一个圆有无数多个外切三角形.
2. 三角形的内心在三角形的内部.
2. 三角形的内心 三角形的内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
3. 三角形内心的性质 三角形的内心到三角形三条边的距离相等,且等于其内切圆的半径.
王奶奶有一块三角形的布料ABC,∠ ACB=90°,她要裁剪一个圆片,已知AC=60 cm,BC=80 cm,为了充分地利用这块布料,使裁剪下来的圆片的直径尽量大些,她应该怎样裁剪?这个圆片的半径是多少?
例6
解题秘方:在三角形中裁剪下的最大圆就是这个三角形的内切圆.
解:如图27.2-23,设△ ABC 的内切圆⊙ O 的半径为r cm,⊙ O 分别切AB,BC,AC 于点D,E,F, 连结OE,OF,则四边形OECF 为正方形. ∴ CE=CF=r cm.
∵∠ ACB=90°,AC=60 cm,BC=80 cm,
∴ AB=100 cm,AF=AD=(60-r)cm,BD=BE=(80-r)cm.
∵ AD+BD=AB,即60-r+80-r=100,
∴ r= =20.
∴她应该裁剪下来这块三角形布料的内切圆,这个圆片的
半径是20 cm.
直角三角形内切圆的半径等于两直角边的和减去斜边之差的一半.
6-1. 如图, ⊙ O 是△ ABC 的内切圆,切点分别为D,E,F.
(1)若AB=9,BC=14,AC=13, 求AD,BE,CF 的长.
解:设AD=x,BE=y,CF=z,由切线长定理可得
AD=AF=x, BD=BE=y, CE=CF=z.
∴x+y=9,y+z=14,x+z=13,
解得x=4,y=5,z=9,
即AD=4,BE=5,CF=9.
(2)若BA=BC=13,AC=24, 求△ ABC 的内切圆的半径.
如图27.2-24, 在△ ABC 中, ∠ A=70 °, 点O 是
△ ABC 的内心,求∠ BOC 的度数.
解题秘方:三角形的内心是三角形三个内角的平分线的交点.
例 7
解:∵∠ A=70°,
∴∠ ABC+ ∠ ACB=180°-70°=110°.
∵点O 是△ ABC 的内心,
∴∠ OBC=∠ABC,∠OCB=∠ ACB.
∴∠ OBC+ ∠ OCB=(∠ ABC+ ∠ ACB)=55°.
∴∠ BOC=180°-55°=125°.
7-1. [中考· 湖州] 如图, 已知△ ABC 的内切圆⊙ O 与BC 边相切于点D, 连结OB,OD. 若∠ ABC=40°,则∠ BOD 的度数是________.
70°
切线
切线
一条切线
判定定理
性质定理
两条切线
切线长定理
三条切线
三角形的内切圆
请完成教材课后习题
作业提升
27.2 与圆有关的位置关系
第27章 圆
27.2.3 切线
逐点
学练
本节小结
作业提升
本节要点
1
学习流程
2
切线的判定定理
切线的性质定理
切线长定理
三角形的内切圆
知识点
切线的判定定理
1
1. 判定定理:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
特别解读
切线必须同时具备两个条件:
1.直线过半径的外端;
2.直线垂直于这条半径.
2. 切线的判定方法:
(1)定义法:与圆有唯一公共点的直线是圆的切线;
(2)数量法:与圆心的距离等于半径的直线是圆的切线;
(3)判定定理法:经过圆的半径的外端且垂直于这条半径的直线是圆的切线.
例 1
如图27.2-17,已知AB 是⊙ O 的直径,AB=4,点C在线段AB 的延长线上,点D 在⊙ O 上,连结CD,且CD=OA,OC=2 ,求证:CD 是⊙ O 的切线.
解题秘方:利用“有切点,连半径,证垂直”判定圆的切线.
证明:如图27.2-17,连结OD.
由题意可知CD=OD=OA= AB=2.
∵ OC=2,∴ OD2+CD2=OC2.
∴∠ ODC=90°,即OD ⊥ CD.
又∵点D 在⊙ O 上,∴ CD 是⊙ O 的切线.
1-1. 如图,点C 是⊙ O上的一点,AB 是⊙ O的直径,∠CAB=∠DCB,那么CD 与⊙ O 的位置关系是( )
相交
相离
相切
相交或相切
C
如图27.2-18,在Rt △ ABC 中,∠ B=90°,∠ BAC
的平分线交BC 于点D,以点D 为圆心,DB 长为半径作⊙ D. 求证:AC 与⊙ D 相切.
例2
解题秘方:利用“无切点,作垂直,证半径”判定圆的切线.
证明:如图27.2-18,过点D 作DF ⊥ AC于点F.
∵∠ B=90°,∴ DB ⊥ AB.
又∵ AD 平分∠ BAC,∴ DF=DB.
∴ AC 与⊙ D 相切.
2-1. 如图,在Rt △ ABC中, ∠ ABC=90 °, 点O 在AB 上,AD ⊥ CO交CO 的延长线于点D,∠ DAO= ∠ACO, 以点O 为圆心,OB 为半径作圆.
(1)求证:AC 是⊙ O的切线;
证明:如图,作OE⊥AC,垂足为E,
∵AD⊥CO,∴∠ADO=90°,
∴∠ADO=∠ABC=90°,
∵∠AOD=∠BOC,∴∠DAO=∠BCO.
∵∠DAO=∠ACO,∴∠BCO=∠ACO.
∵OB⊥BC,OE⊥AC,∴OE=OB,
∵OB是半径,∴AC是⊙O的切线.
(2)已知CB=6,AB=8,求OC 的长.
解:∵∠OBC=∠OEC,∠BCO=∠ACO,OC=OC,
∴△OBC≌△OEC,∴BC=EC=6.
知识点
切线的性质定理
2
1. 性质定理 圆的切线垂直于经过切点的半径.
2. 切线的性质 (1)切线和圆只有一个公共点.
(2)圆心到切线的距离等于半径.
(3)圆的切线垂直于过切点的半径.
(4)经过圆心且垂直于切线的直线必过切点(找切点用).
(5)经过切点且垂直于切线的直线必过圆心(找圆心用).
特别提醒
切线的判定定理与性质定理的区别:切线的判定定理是在未知相切而要证明相切的情况下使用;切线的性质定理是在已知相切而要推得其他的结论时使用.它们是一个互逆的过程,不要混淆.
如图27.2-19,AB 为⊙ O 的直径,PD 切⊙ O 于点C,交AB 的延长线于点D,且∠ D=2 ∠ CAD.
例 3
(1)求∠ D 的度数.
解题秘方:利用“等半径”得等腰三角形。
解:如图27.2-19,连结OC.
∵ AO=CO,∴∠ OAC= ∠ ACO.
∴∠ COD=2 ∠ CAD.
又∵∠ D=2 ∠ CAD,∴∠ D= ∠ COD.
∵ PD 切⊙ O 于点C,
∴ OC ⊥ PD,即∠ OCD=90° . ∴∠ D=45° .
(2)若CD=2,求BD 的长.
解:由(1)可知△ OCD 是等腰直角三角形.
∴ OC=CD=2.
由勾股定理,得OD= = =2,
∴ BD=OD-OB=2-2.
解题秘方:利用“切线垂直于过切点的半径”构造直角三角形,再结合相关性质求解.
3-1. [中考· 泰安] 如图, 在△ ABC 中,∠ B=90 °, ⊙ O 过点A,C, 与AB 交于点D,与BC 相切于点C, 若∠A=32 °, 则∠ ADO=_______.
64°
如图27.2-20,已知BC 是⊙ O 的直径,AC 切⊙O于点C,AB 交⊙ O 于点D,E 为AC 的中点,连结DE.
例4
(1)若AD=DB,OC=5,求切线AC 的长;
解题秘方:构造直径所对的圆周角,利用直径所对的圆周角是直角求解;
解:连结CD,如图27.2-20.
∵ BC 是⊙ O 的直径,
∴∠ BDC=90°,即CD ⊥ AB.
∵ AD=DB,∴ AC=BC=2OC=10.
(2)求证:DE 是⊙ O 的切线.
解题秘方:利用“连半径,证垂直”求解.
证明:连结OD,如图27.2-20.
∵∠ ADC=90°,E 为AC 的中点,
∴ DE=EC= AC. ∴∠ 1 =∠ 2.
∵ OD=OC,∴∠ 3 =∠ 4.
∵ AC 切⊙ O 于点C,∴ AC ⊥ OC.
∴∠ 1+ ∠ 3= ∠ 2+ ∠ 4 = 90°,即DE ⊥ OD.
又∵ OD 是⊙ O 的半径,∴ DE 是⊙ O 的切线.
4-1. [中考·十堰] 如图,在△ ABC 中,AB=AC,D 为AC 上一点,以CD 为直径的⊙ O 与AB 相切于点E,交BC于点F,FG ⊥ AB,垂足为G.
(1)求证:FG 是⊙ O的切线;
证明:如图,连结OF.
∵AB=AC,∴∠B=∠C,∵OF=OC,
∴∠C=∠OFC,
∴∠OFC=∠B,∴OF∥AB.
∵FG⊥AB,∴FG⊥OF.
又∵OF是⊙O的半径,∴FG是⊙O的切线.
(2)若BG=1,BF=3,求CF 的长.
解:如图,连结OE,过点O作OH⊥CF于点H.
知识点
切线长定理
3
1. 切线长定义:我们把圆的切线上某一点与切点之间的线段的长叫做这点到圆的切线长.
切线是直线,不可度量;切线长是切线上切点与切点外另一点之间的线段的长,可以度量.
2. 切线长定理:
过圆外一点所画的圆的两条切线,它们的切线长相等,这一点和圆心的连线平分这两条切线的夹角.
特别解读
经过圆上一点作圆的切线,有且只有一条,过切点的半径垂直于这条切线;经过圆外一点作圆的切线,有两条,这点和两个切点之间的两条线段长相等.
3. 示例:如图27.2-21 是切线长定理的一个基本图形, 可以直接得到结论:(1)PO ⊥ AB;
(2)AO ⊥ AP,BO ⊥ BP;
(3)AP=BP;
(4)∠ 1= ∠ 2= ∠ 3= ∠ 4;
(5)AD=BD;
(6)AC = BC等.
︵
︵
如图27.2-22,PA,PB,DE 分别切⊙ O 于点A,B,C,点D 在PA 上,点E 在PB 上.
例 5
解题秘方:紧扣切线长定理,切线的性质定理,四边形的内角和及角平分线的判定定理求解.
解:∵ PA,PB,DE 分别切⊙ O 于点A,B,C,
∴ PB=PA=10,DA=DC,EC=EB.
∴ PD+DE+PE=PD+DC+CE+PE=PD+DA+EB+PE=PA+
PB=10+10=20.
∴△ PDE 的周长为20.
(1)若PA=10,求△ PDE 的周长;
解:如图27.2-22,连结OA,OC,OB.
∵ PA,PB,DE 是⊙ O 的切线,
∴ OA ⊥ PA,OB ⊥ PB,OC ⊥ DE.
∴∠ DAO= ∠ EBO=90°.∴∠ P+ ∠ AOB=180°.
∴∠ AOB=180°-50°=130°.
易知∠ AOD= ∠ DOC,∠ COE= ∠ BOE,
∴∠ DOE=∠ AOB=×130°=65°.
(2)若∠ P=50°,求∠ DOE 的度数.
5-1. (易错题) 如图,直线AB,AD 分别与⊙ O 相切于点B,D,C 为⊙ O 上一点, 且∠ BCD=130°,则∠ A的度数是( )
70°
85°
80°
100°
C
5-2. 如图,PA,PB切⊙ O 于A,B 两点,CD 切⊙ O 于点E,交PA,PB 于点C,D. 若⊙ O 的半径为2,△ PCD 的周长等于4 ,则线段AB 的长是________.
知识点
三角形的内切圆
4
1. 三角形的内切圆 与三角形各边都相切的圆叫做这个三角形的内切圆,这个三角形叫做这个圆的外切三角形.
要点解读
1. 一个三角形有一个内切圆,而一个圆有无数多个外切三角形.
2. 三角形的内心在三角形的内部.
2. 三角形的内心 三角形的内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心.
3. 三角形内心的性质 三角形的内心到三角形三条边的距离相等,且等于其内切圆的半径.
王奶奶有一块三角形的布料ABC,∠ ACB=90°,她要裁剪一个圆片,已知AC=60 cm,BC=80 cm,为了充分地利用这块布料,使裁剪下来的圆片的直径尽量大些,她应该怎样裁剪?这个圆片的半径是多少?
例6
解题秘方:在三角形中裁剪下的最大圆就是这个三角形的内切圆.
解:如图27.2-23,设△ ABC 的内切圆⊙ O 的半径为r cm,⊙ O 分别切AB,BC,AC 于点D,E,F, 连结OE,OF,则四边形OECF 为正方形. ∴ CE=CF=r cm.
∵∠ ACB=90°,AC=60 cm,BC=80 cm,
∴ AB=100 cm,AF=AD=(60-r)cm,BD=BE=(80-r)cm.
∵ AD+BD=AB,即60-r+80-r=100,
∴ r= =20.
∴她应该裁剪下来这块三角形布料的内切圆,这个圆片的
半径是20 cm.
直角三角形内切圆的半径等于两直角边的和减去斜边之差的一半.
6-1. 如图, ⊙ O 是△ ABC 的内切圆,切点分别为D,E,F.
(1)若AB=9,BC=14,AC=13, 求AD,BE,CF 的长.
解:设AD=x,BE=y,CF=z,由切线长定理可得
AD=AF=x, BD=BE=y, CE=CF=z.
∴x+y=9,y+z=14,x+z=13,
解得x=4,y=5,z=9,
即AD=4,BE=5,CF=9.
(2)若BA=BC=13,AC=24, 求△ ABC 的内切圆的半径.
如图27.2-24, 在△ ABC 中, ∠ A=70 °, 点O 是
△ ABC 的内心,求∠ BOC 的度数.
解题秘方:三角形的内心是三角形三个内角的平分线的交点.
例 7
解:∵∠ A=70°,
∴∠ ABC+ ∠ ACB=180°-70°=110°.
∵点O 是△ ABC 的内心,
∴∠ OBC=∠ABC,∠OCB=∠ ACB.
∴∠ OBC+ ∠ OCB=(∠ ABC+ ∠ ACB)=55°.
∴∠ BOC=180°-55°=125°.
7-1. [中考· 湖州] 如图, 已知△ ABC 的内切圆⊙ O 与BC 边相切于点D, 连结OB,OD. 若∠ ABC=40°,则∠ BOD 的度数是________.
70°
切线
切线
一条切线
判定定理
性质定理
两条切线
切线长定理
三条切线
三角形的内切圆
请完成教材课后习题
作业提升
