数学人教A版(2019)必修第一册4.4.2对数函数的图象和性质(共39张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.4.2对数函数的图象和性质(共39张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 07:21:59 | ||
图片预览








文档简介
(共39张PPT)
4.4.2 对数函数的图像和性质
第四章 指数函数与对数函数
学习目标
1.通过具体对数函数图像,掌握对数函数的图像和性质
特征,并能解决问题。
2.知道同底的对数函数与指数函数互为反函数。
我们该如何去研究对数函数的性质呢?
提出问题
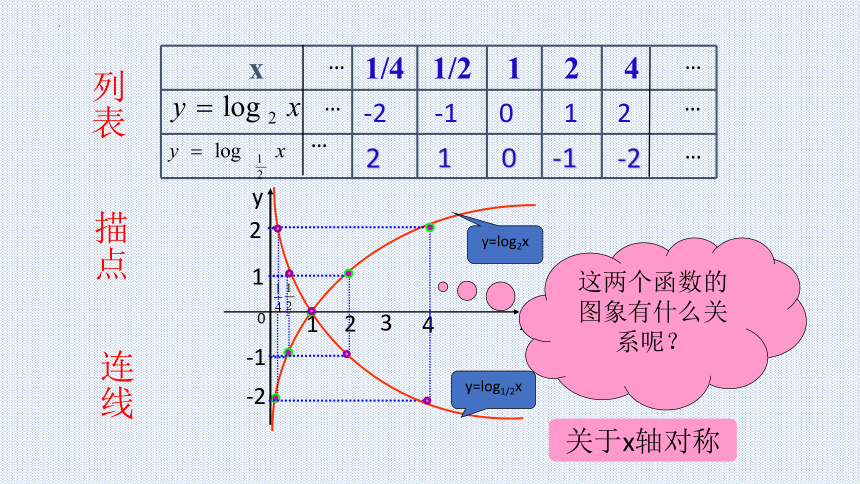
列表
x 1/4 1/2 1 2 4
2 1 0 -1 -2
-2 -1 0 1 2
…
…
…
…
…
…
作图步骤:
1. 列表 2. 描点 3. 连线
问题1. 画出函数 和 的图象。
问题探究
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
x 1/4 1/2 1 2 4
-2 -1 0 1 2
2 1 0 -1 -2
…
…
…
…
…
…
列表
问题探究
问题2:我们知道,底数互为倒数的两个指数函数的图象关
于 y轴对称.对于底数互为倒数的两个对数函数,
比如 和 ,它们的图象是否也有某种对称关系呢?可否利用其中一个函数的图象画出另一个函数的图象?
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
y=log1/2x
y=log2x
x 1/4 1/2 1 2 4
…
…
…
…
…
…
-2 -1 0 1 2
2 1 0 -1 -2
列表
这两个函数的图象有什么关系呢?
关于x轴对称
问题3:底数a(a>0,且a≠1)的若干个不同的值,在同一直角坐标系内画出相应的对数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?
由此你能概括出对数函数 (a>0,且a≠1)的值域和性质吗?
问题探究
问题探究
y=logax(a>1)的图象
x
o
(1,0)
x =1
y = log x (a>1)
a
y
问题探究
y=logax(0x
y
x = 1
(1,0)
y = log x
(0a
o
问题探究
a>1 0<a<1
图 象
性 质 ⑴定义域: ⑵值域: ⑶过特殊点: ⑷单调性 : ⑷单调性:
(0,+∞)
R
过点(1,0),即x=1时y=0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
x
o
(1,0)
x =1
y
x
y
x = 1
(1,0)
o
当 x > 1 时,y > 0;
当 0 < x < 1 时, y < 0.
当 x > 1 时,y < 0;
当 0 < x < 1 时, y > 0.
对数函数的图象和性质
对数函数的性质的助记口诀:
对数增减有思路, 函数图象看底数;
底数只能大于0, 等于1来也不行;
底数若是大于1, 图象从下往上增;
底数0到1之间, 图象从上往下减;
无论函数增和减, 图象都过(1,0)点.
记忆口诀
问题探究
【即时训练】
1.判断正误(正确的打“√”,错误的打“×”)
(1)对数函数 与 的图象关于 轴对称.( )
×
(2)对数函数的图象都过定点 .( )
×
(3)若函数 是减函数,则 .( )
√
2.函数 ,且 恒过定点______.
解析:当 时, ,故恒过定点 .
知识点二 反函数
1.定义:一般地,指数函数 ,且 与对数函数__________
,且 互为反函数.
2.性质:
(1)互为反函数的两个函数图象关于直线______对称.
(2)反函数的定义域是原函数的______,反函数的值域是原函数的_____
___.
值域
定义域
【即时训练】
1.若函数 是函数 的反函数,则 的值为 ( )
A. B. C.1 D.
解析:选B.依题意,函数 是函数 的反函数,所以
, .故选B.
√
2.函数 ,且 的反函数的图象过点 ,则 的
值为__.
解析:由函数 ,且 的反函数为 ,且
,所以函数 的图象过点 ,即 ,则 .
考点一 比较对数值的大小
例1 比较下列各组值的大小:
(1) , ;
【解】因为函数 在 上是减函数,且 ,所以
.
(2) , ;
【解】 因为函数 在 上是增函数,且 ,所以
.
(3) , .
【解】 因为 , ,所以 .
比较对数值大小常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
[注意] 比较数的大小时先利用性质比较出与0或1的大小.
【跟踪训练】
1.已知实数 , , ,则( )
A. B. C. D.
解析:选A.因为 , ,
,所以 .故选A.
√
2.若 , , ,则 , , 从大到小的顺序为
__________.
解析:由于 ,即 .
由 ,即 .所以 .
考点二 解对数型不等式
例2 解下列不等式:
(1) ;
【解】由对数函数的单调性和定义域,可得 解得
,所以不等式的解集为 .
(2) ;
【解】 因为 为减函数,所以
,
解得 ,所以不等式的解集为 .
(3) .
【解】 因为 或
所以原不等式的解集为 .
两类对数不等式的解法
(1)形如 的不等式.
①当 时,可转化为 ;
②当 时,可转化为 .
(2)形如 的不等式可变形为 .
①当 时,可转化为 ;
②当 时,可转化为 .
[注意] 解决与对数函数相关的问题时要遵循定义域优先原则.
【跟踪训练】
1.已知 ,那么 的取值范围是( )
A. B.
C. D.
√
解析:选 ,
当 时, 为增函数,故 ;
当 时, 为减函数,故 ,
即 .
所以 的取值范围是 .故选D.
2.不等式 的解集为________.
解析:由 ,有 ,根据对数函数的单调性有 ,即 .
考点三 作对数(型)函数的图象
例3 画出下列函数的图象,并根据图象写出函数的定义域、值域以及单调性:
(1) ;
【解】函数 的图象如图①.其定义域为 ,值域为 ,
在区间 上是增函数.
图①
(2) .
图②
【解】 其图象如图②.
其定义域为 ,值域为 ,在 上单调递减,在 上单调递增.
(1)对数型函数的图象一般以函数 的图象为基础,通过平移、
对称变换得到.
(2)两种常见的对称变换:
①含有绝对值的函数的图象变换,一般地, 的图象是保留
的图象在 轴上方的部分,并把 轴下方的部分以 轴为对称轴
翻折到 轴上方得到;
的图象与 的图象关于 轴对称, 的图象
与 的图象关于 轴对称.
【跟踪训练】
已知 ,且 满足 ,试画出函数 的
图象.
解:因为 ,所以 ,即 ,
故
所以函数 的图象如图所示.
1.函数 的大致图象为( )
A.&1& B.&2& C.&3& D.&4&
解析:选A.由对数函数性质知 为增函数,故排除B、D;当
时, ,即函数过点 ,排除C. 故选A.
√
2.已知函数 的反函数为 ,则 的值为( )
A. B.1 C.16 D.2
解析:选A.由于函数 的反函数为 ,则 ,因此, .故选A.
√
3.已知 , , ,则 , , 的大小关系为
( )
A. B. C. D.
解析:选B.因为 , , ,所以 .故选B.
√
4.函数 ,且 恒过定点 ,则
___.
2
解析:由题意知 恒成立,解得 .
5.不等式 的解集是______.
解析:因为 在 上是增函数, ,所以 ,解得 .
4.4.2 对数函数的图像和性质
第四章 指数函数与对数函数
学习目标
1.通过具体对数函数图像,掌握对数函数的图像和性质
特征,并能解决问题。
2.知道同底的对数函数与指数函数互为反函数。
我们该如何去研究对数函数的性质呢?
提出问题
列表
x 1/4 1/2 1 2 4
2 1 0 -1 -2
-2 -1 0 1 2
…
…
…
…
…
…
作图步骤:
1. 列表 2. 描点 3. 连线
问题1. 画出函数 和 的图象。
问题探究
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
x 1/4 1/2 1 2 4
-2 -1 0 1 2
2 1 0 -1 -2
…
…
…
…
…
…
列表
问题探究
问题2:我们知道,底数互为倒数的两个指数函数的图象关
于 y轴对称.对于底数互为倒数的两个对数函数,
比如 和 ,它们的图象是否也有某种对称关系呢?可否利用其中一个函数的图象画出另一个函数的图象?
描点
连线
2
1
-1
-2
1
2
4
0
y
x
3
y=log1/2x
y=log2x
x 1/4 1/2 1 2 4
…
…
…
…
…
…
-2 -1 0 1 2
2 1 0 -1 -2
列表
这两个函数的图象有什么关系呢?
关于x轴对称
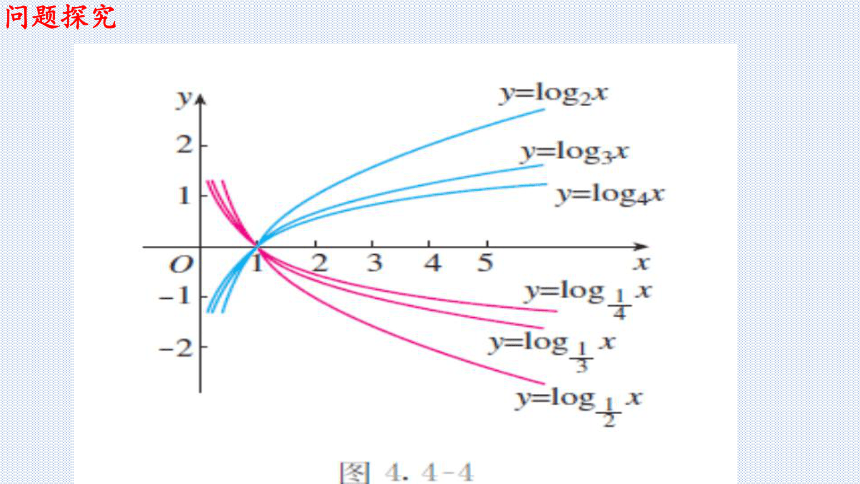
问题3:底数a(a>0,且a≠1)的若干个不同的值,在同一直角坐标系内画出相应的对数函数的图象.观察这些图象的位置、公共点和变化趋势,它们有哪些共性?
由此你能概括出对数函数 (a>0,且a≠1)的值域和性质吗?
问题探究
问题探究
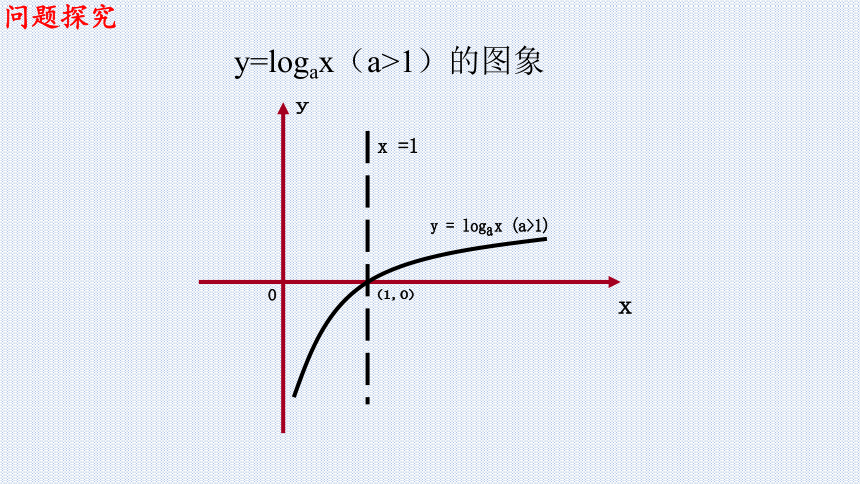
y=logax(a>1)的图象
x
o
(1,0)
x =1
y = log x (a>1)
a
y
问题探究
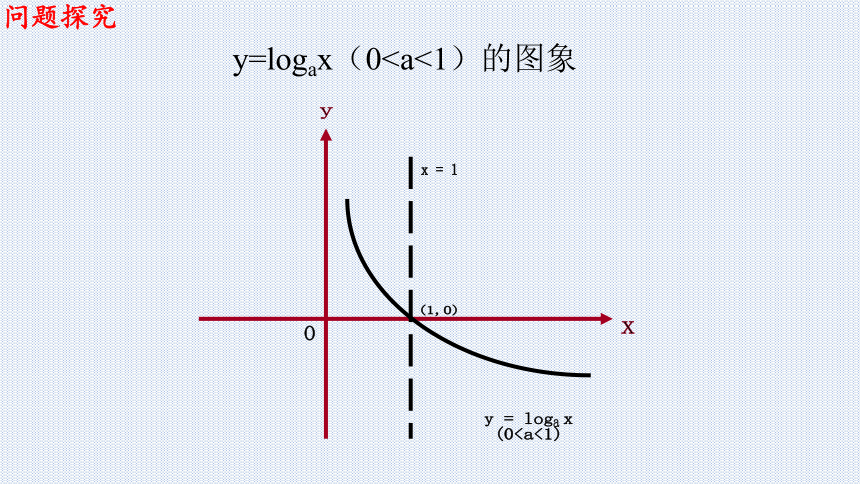
y=logax(0
y
x = 1
(1,0)
y = log x
(0
o
问题探究
a>1 0<a<1
图 象
性 质 ⑴定义域: ⑵值域: ⑶过特殊点: ⑷单调性 : ⑷单调性:
(0,+∞)
R
过点(1,0),即x=1时y=0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
x
o
(1,0)
x =1
y
x
y
x = 1
(1,0)
o
当 x > 1 时,y > 0;
当 0 < x < 1 时, y < 0.
当 x > 1 时,y < 0;
当 0 < x < 1 时, y > 0.
对数函数的图象和性质
对数函数的性质的助记口诀:
对数增减有思路, 函数图象看底数;
底数只能大于0, 等于1来也不行;
底数若是大于1, 图象从下往上增;
底数0到1之间, 图象从上往下减;
无论函数增和减, 图象都过(1,0)点.
记忆口诀
问题探究
【即时训练】
1.判断正误(正确的打“√”,错误的打“×”)
(1)对数函数 与 的图象关于 轴对称.( )
×
(2)对数函数的图象都过定点 .( )
×
(3)若函数 是减函数,则 .( )
√
2.函数 ,且 恒过定点______.
解析:当 时, ,故恒过定点 .
知识点二 反函数
1.定义:一般地,指数函数 ,且 与对数函数__________
,且 互为反函数.
2.性质:
(1)互为反函数的两个函数图象关于直线______对称.
(2)反函数的定义域是原函数的______,反函数的值域是原函数的_____
___.
值域
定义域
【即时训练】
1.若函数 是函数 的反函数,则 的值为 ( )
A. B. C.1 D.
解析:选B.依题意,函数 是函数 的反函数,所以
, .故选B.
√
2.函数 ,且 的反函数的图象过点 ,则 的
值为__.
解析:由函数 ,且 的反函数为 ,且
,所以函数 的图象过点 ,即 ,则 .
考点一 比较对数值的大小
例1 比较下列各组值的大小:
(1) , ;
【解】因为函数 在 上是减函数,且 ,所以
.
(2) , ;
【解】 因为函数 在 上是增函数,且 ,所以
.
(3) , .
【解】 因为 , ,所以 .
比较对数值大小常用的四种方法
(1)同底数的利用对数函数的单调性.
(2)同真数的利用对数函数的图象或用换底公式转化.
(3)底数和真数都不同,找中间量.
(4)若底数为同一参数,则根据底数对对数函数单调性的影响,对底数进行分类讨论.
[注意] 比较数的大小时先利用性质比较出与0或1的大小.
【跟踪训练】
1.已知实数 , , ,则( )
A. B. C. D.
解析:选A.因为 , ,
,所以 .故选A.
√
2.若 , , ,则 , , 从大到小的顺序为
__________.
解析:由于 ,即 .
由 ,即 .所以 .
考点二 解对数型不等式
例2 解下列不等式:
(1) ;
【解】由对数函数的单调性和定义域,可得 解得
,所以不等式的解集为 .
(2) ;
【解】 因为 为减函数,所以
,
解得 ,所以不等式的解集为 .
(3) .
【解】 因为 或
所以原不等式的解集为 .
两类对数不等式的解法
(1)形如 的不等式.
①当 时,可转化为 ;
②当 时,可转化为 .
(2)形如 的不等式可变形为 .
①当 时,可转化为 ;
②当 时,可转化为 .
[注意] 解决与对数函数相关的问题时要遵循定义域优先原则.
【跟踪训练】
1.已知 ,那么 的取值范围是( )
A. B.
C. D.
√
解析:选 ,
当 时, 为增函数,故 ;
当 时, 为减函数,故 ,
即 .
所以 的取值范围是 .故选D.
2.不等式 的解集为________.
解析:由 ,有 ,根据对数函数的单调性有 ,即 .
考点三 作对数(型)函数的图象
例3 画出下列函数的图象,并根据图象写出函数的定义域、值域以及单调性:
(1) ;
【解】函数 的图象如图①.其定义域为 ,值域为 ,
在区间 上是增函数.
图①
(2) .
图②
【解】 其图象如图②.
其定义域为 ,值域为 ,在 上单调递减,在 上单调递增.
(1)对数型函数的图象一般以函数 的图象为基础,通过平移、
对称变换得到.
(2)两种常见的对称变换:
①含有绝对值的函数的图象变换,一般地, 的图象是保留
的图象在 轴上方的部分,并把 轴下方的部分以 轴为对称轴
翻折到 轴上方得到;
的图象与 的图象关于 轴对称, 的图象
与 的图象关于 轴对称.
【跟踪训练】
已知 ,且 满足 ,试画出函数 的
图象.
解:因为 ,所以 ,即 ,
故
所以函数 的图象如图所示.
1.函数 的大致图象为( )
A.&1& B.&2& C.&3& D.&4&
解析:选A.由对数函数性质知 为增函数,故排除B、D;当
时, ,即函数过点 ,排除C. 故选A.
√
2.已知函数 的反函数为 ,则 的值为( )
A. B.1 C.16 D.2
解析:选A.由于函数 的反函数为 ,则 ,因此, .故选A.
√
3.已知 , , ,则 , , 的大小关系为
( )
A. B. C. D.
解析:选B.因为 , , ,所以 .故选B.
√
4.函数 ,且 恒过定点 ,则
___.
2
解析:由题意知 恒成立,解得 .
5.不等式 的解集是______.
解析:因为 在 上是增函数, ,所以 ,解得 .
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
