苏科版八年级数学上册5.2平面直角坐标系 提优训练(二)(含答案)
文档属性
| 名称 | 苏科版八年级数学上册5.2平面直角坐标系 提优训练(二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 287.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 14:53:55 | ||
图片预览



文档简介
2023-2024学年苏科版八年级数学上《5.2平面直角坐标系》提优训练(二)
(时间:100分钟 满分:120分)
一.选择题(共30分)
1.点P1(a﹣1,2024)和P2(2023,b﹣1)关于x轴对称,则(a+b)2021的值为( )
A.﹣1 B.1 C.0 D.无法确定
2.已知两点A(a,5),B(﹣1,b)且直线AB∥x轴,则( )
A.a可取任意实数,b=5 B.a=﹣1,b可取任意实数
C.a≠﹣1,b=5 D.a=﹣1,b≠5
3.在平面直角坐标系xOy中,过点P(﹣2,3)作PA⊥y轴,垂足为点A,那么PA的长为( )
A.2 B.3 C.5 D.
4.在平面直角坐标系中,将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是( )
A.(3,8) B.(1,8) C.(1,4) D.(3,4)
5.在平面直角坐标系中点P(﹣20,a)与点Q(b,13)关于y轴对称,则﹣a+b的值为( )
A.﹣33 B.33 C.﹣7 D.7
6、若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f (1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g(f(3,﹣4))的值为( )
A.(3,﹣4) B.(﹣3,4) C.(3,4) D.(﹣3,﹣4)
7.如图,在平面直角坐标系中,点A是x轴正半轴上的一个动点,点C是y轴正半轴上的点,BC⊥AC于点C.已知AC=16,BC=6.点B到原点的最大距离为( )
A.22 B.18 C.14 D.10
第7题图 第8题图 第9题图 第10题图
8.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( C )
A.2 B.3 C.4 D.5
9.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2 B.3 C.4 D.5
10.如图,平面直角坐标系xOy中,点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°.在x轴上取一点P(m,0),过点P作直线l垂直于直线OA,将OB关于直线l的对称图形记为O′B′,当O′B′和过A点且平行于x轴的直线有交点时,m的取值范围为( )
A.m≥4 B.m≤6 C.4<m<6 D.4≤m≤6
二.填空题(共30分)
11.点A(3,﹣2)关于x轴对称的点的坐标是 .
12.点P(2,﹣3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P′的坐标是 .
13.在平面直角坐标系中,A,B,C三点的坐标分别是A(5,0),B(0,3),C(5,3),O为坐标原点,点E在线段BC上.若△AEO为等腰三角形,点E的坐标为_______________.
14.已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)的坐标为 .
15.在平面直角坐标系中,若A(x1,y1)、B(x2,y2),则AB=,若M(﹣4,1)、N(2,﹣1),则MN= .
16.已知点A在x轴的下方,且到x轴的距离为5,到y轴的距离为3,则点A的坐标为________.
17.已知点M(3,2)与点N(x,y)在同一条平行于x轴的直线上,且点N到y轴的距离为8,则点N的坐标为________.
18.如图,在平面直角坐标系中,第1次将边长为1个单位长度的正方形OABC绕点O逆时针旋转45°后,得到正方形OA1B1C1;第2次将正方形OA1B1C1绕点O逆时针旋转45°后,得到正方形OA2B2C2;……,按此规律,绕点O旋转得到正方形OA2 023B2 024C2 023,则点B2 024的坐标为 .
第18题图 第19题图
19.如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为 .
20.在平面直角坐标系中,已知点A(-3,0),B(3,0),点C在坐标轴上,且AC+BC=10,写出满足条件的所有点C的坐标:________.
三.解答题(60分)
21.(8分)已知a,b都是实数,设点P(a+2,),且满足3a=2+b,我们称点P为“梦之点”.
(1)判断点A(3,2)是否为“梦之点”,并说明理由.
(2)若点M(m﹣1,3m+2)是“梦之点”,请判断点M在第几象限,并说明理由.
22.(8分)在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”,例如,点P(1,4)的3级关联点”为Q(3×1+4,1+3×4)即Q(7,13),若点B的“2级关联点”是B(3,3).
(1)求点B的坐标;
(2)已知点M(m﹣1,2m)的“﹣3级关联点”N位于y轴上,求N的坐标.
23、(8分)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.
24.(12分)已知点P(2m+4,m﹣1),请分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣4)点,且与y轴平行的直线上;
(3)点P到两坐标轴的距离相等.
25.(12分)已知点M(3a-2,a+6).
(1)若点M在x轴上,求点M的坐标
(2)变式一:已知点M(3a-2,a+6),点N(2,5),且直线MN∥x轴,求点M的坐标.
(3)变式二:已知点M(3a-2,a+6),若点M到x轴、y轴的距离相等,求点M的坐标.
26.(12分)问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
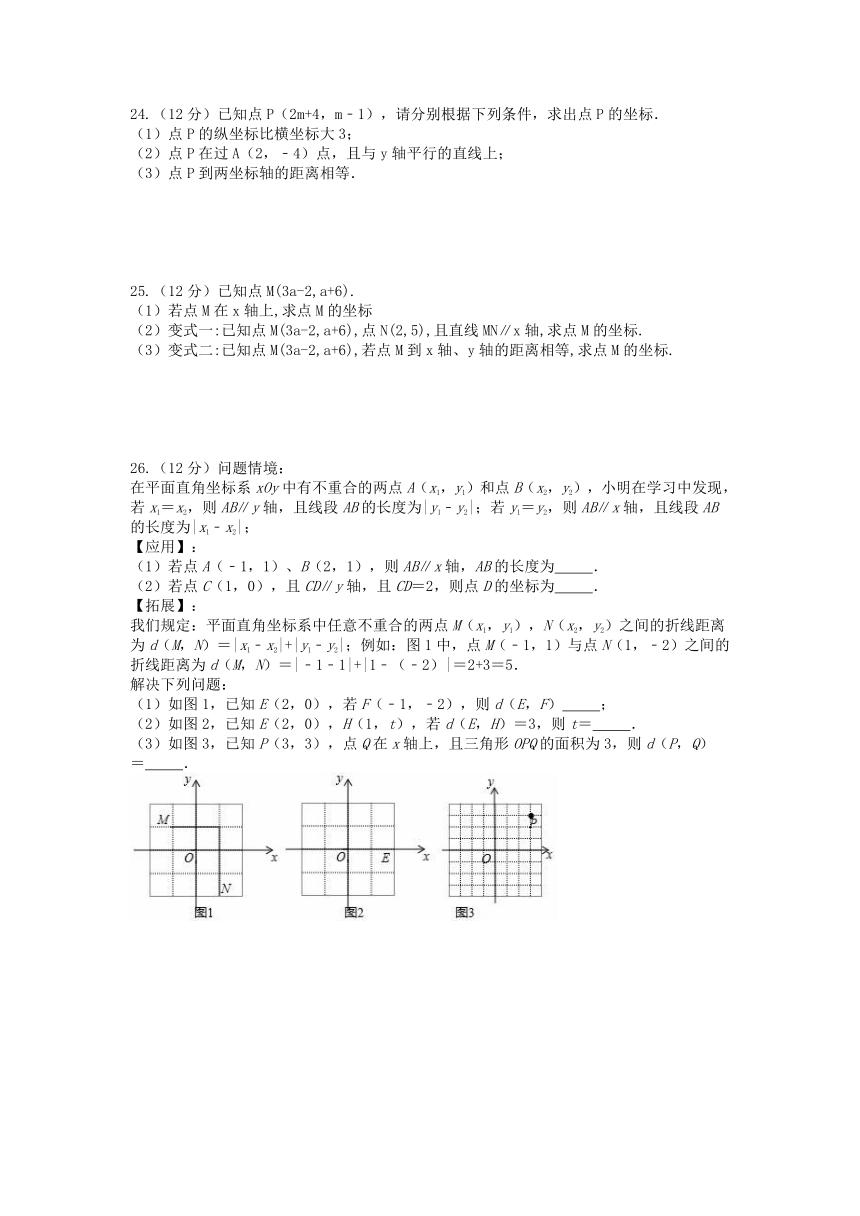
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
教师样卷
一.选择题(共30分)
1.点P1(a﹣1,2024)和P2(2023,b﹣1)关于x轴对称,则(a+b)2021的值为( A )
A.﹣1 B.1 C.0 D.无法确定
2.已知两点A(a,5),B(﹣1,b)且直线AB∥x轴,则( C )
A.a可取任意实数,b=5 B.a=﹣1,b可取任意实数
C.a≠﹣1,b=5 D.a=﹣1,b≠5
3.在平面直角坐标系xOy中,过点P(﹣2,3)作PA⊥y轴,垂足为点A,那么PA的长为( A )
A.2 B.3 C.5 D.
4.在平面直角坐标系中,将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是( B )
A.(3,8) B.(1,8) C.(1,4) D.(3,4)
5.在平面直角坐标系中点P(﹣20,a)与点Q(b,13)关于y轴对称,则﹣a+b的值为( D )
A.﹣33 B.33 C.﹣7 D.7
解:∵在平面直角坐标系内点P(﹣20,a)与点Q(b,13)关于y轴对称,∴a=13,b=20,则﹣a+b=﹣13+20=7.故选:D.
6、若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f (1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g(f(3,﹣4))的值为( B )
A.(3,﹣4) B.(﹣3,4) C.(3,4) D.(﹣3,﹣4)
解:g(f(3,﹣4))=g(﹣3,﹣4)=(﹣3,4),故选:B.
7.如图,在平面直角坐标系中,点A是x轴正半轴上的一个动点,点C是y轴正半轴上的点,BC⊥AC于点C.已知AC=16,BC=6.点B到原点的最大距离为( B )
A.22 B.18 C.14 D.10
解:取AC的中点D,连接OD,BD,OB,如图,∵D为AC的中点,∠AOC=90°,∴OD=CD=AC=8.∵∠ACB=90°,∴BD===10.当O,D,B三点不在一条直线上时,OB<OD+BD=8+10=18,当O,D,B三点在一条直线上时,OB=OD+BD=8+10=18,∴当O,D,B三点在一条直线上时,点B到原点的最大距离为18.故选:B.
8.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( C )
A.2 B.3 C.4 D.5
解:如图,∵到直线l1的距离是1的点在与直线l1平行且与l1的距离是1的两条平行线a1、a2上,到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线b1、b2上,∴“距离坐标”是(1,2)的点是M1、M2、M3、M4,一共4个.故选C.
9.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( A )
A.2 B.3 C.4 D.5
解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A、B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.故选:A.
10.如图,平面直角坐标系xOy中,点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°.在x轴上取一点P(m,0),过点P作直线l垂直于直线OA,将OB关于直线l的对称图形记为O′B′,当O′B′和过A点且平行于x轴的直线有交点时,m的取值范围为( D )
A.m≥4 B.m≤6 C.4<m<6 D.4≤m≤6
解:如右图所示,当直线l垂直平分OA时,O′B′和过A点且平行于x轴的直线有交点,
∵点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°,∴∠BAO=30°,OB=2,
∴OA=4,∵直线l垂直平分OA,点P(m,0)是直线l与x轴的交点,∴OP=4,∴当m=4;作BB″∥OA,交过点A且平行于x轴的直线与B″,当直线l垂直平分BB″和过A点且平行于x轴的直线有交点,∵四边形OBB″O′是平行四边形,∴此时点P与x轴交点坐标为(6,0),由图可知,当OB关于直线l的对称图形为O′B′到O″B″的过程中点P符合题目中的要求,∴m的取值范围是4≤m≤6,故选:D.
二.填空题(共30分)
11.点A(3,﹣2)关于x轴对称的点的坐标是 (3,2) .
12.点P(2,﹣3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P′的坐标是 (﹣2,﹣2) .
13.在平面直角坐标系中,A,B,C三点的坐标分别是A(5,0),B(0,3),C(5,3),O为坐标原点,点E在线段BC上.若△AEO为等腰三角形,点E的坐标为__(1,3),(2.5,3) ,(4,3)_____________.
解: 画出图形如解图.①若A为顶角顶点,则AE=AO,故点E(1,3).②若E为顶角顶点,则EO=EA,故点E(2.5,3).③若O为顶角顶点,则OE=OA,故点E(4,3).
14.已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)的坐标为 (5,﹣3) .
解:∵A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,∴a﹣5=0,b+3=0,解得:a=5,b=﹣3,∴C(a,b)的坐标为:(5,﹣3).
15.在平面直角坐标系中,若A(x1,y1)、B(x2,y2),则AB=,若M(﹣4,1)、N(2,﹣1),则MN= 2 .
解:∵M(﹣4,1)、N(2,﹣1),∴MN==2,故答案为:2.
16.已知点A在x轴的下方,且到x轴的距离为5,到y轴的距离为3,则点A的坐标为__(3,﹣5)或(﹣3,﹣5) ______.
解:∵点A在x轴的下方,且到x轴的距离为5,到y轴的距离为3,∴点A的纵坐标为:﹣5,横坐标为:±3,故点A的坐标为:(3,﹣5)或(﹣3,﹣5).
故答案为:(3,﹣5)或(﹣3,﹣5).
17.已知点M(3,2)与点N(x,y)在同一条平行于x轴的直线上,且点N到y轴的距离为8,则点N的坐标为_(8,2)或(-8,2)_______.
解:由点M(3,2)与点N(x,y)在同一条平行于x轴的直线上可得:y=2;由点N到y轴的距离为8可得x=±8,所以点N的坐标为(8,2)或(-8,2).
故答案为(8,2)或(-8,2).
18.如图,在平面直角坐标系中,第1次将边长为1个单位长度的正方形OABC绕点O逆时针旋转45°后,得到正方形OA1B1C1;第2次将正方形OA1B1C1绕点O逆时针旋转45°后,得到正方形OA2B2C2;……,按此规律,绕点O旋转得到正方形OA2 023B2 024C2 023,则点B2 024的坐标为 (1,1).
解:∵四边形OABC是正方形,OA=1,∴B(1,1),如图,连结OB,根据勾股定理可得OB=,
由旋转可得OB=OB1=OB2=…=OB2 020=,∠AOB=∠BOB1=∠B1OB2=…=∠B2 023OB2 024=45°,
∴B1(0,),B2(-1,1),B3(-,0),B4(-1,-1),B5(0,-),B6(1,-1),B7(,0),B8(1,1),B9(0,),……,∴8次一循环,∵2 024÷8=253,∴点B2 024的坐标为(1,1).
第18题图 第19题图
19.如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为 ﹣()2023 .
解:∵A1(1,0),A2[0,()1],A3[﹣()2,0].A4[0,﹣()3],A5[()4,0]…,∴序号除以4整除的话在y轴的负半轴上,余数是1在x轴的正半轴上,余数是2在y轴的正半轴上,余数是3在x轴的负半轴上,∵2024÷4=506,∴A2024在y轴的负半轴上,纵坐标为﹣()2023.故答案为﹣()2023.
20.在平面直角坐标系中,已知点A(-3,0),B(3,0),点C在坐标轴上,且AC+BC=10,写出满足条件的所有点C的坐标:___ (-5,0),(5,0),(0,4),(0,-4) _____.
解:第一种情况:当点C在x轴左半轴时,点C在点A的左侧. 若C在点A的右侧,只能当A与C重合时取最大值6,则AC+BC<6,与题意不符.设点C的坐标为(x,0).∵AC+BC=10,点A(-3,0),B(3,0),∴(-3-x)+(3-x)=10.解得,x=-5.∴点C的坐标为(-5,0),点A(-3,0),B(3,0),第二种情况:当点C在x轴左半轴时,点C在点B的右侧.若C在点B的左侧,只能当与B,C重合时取最大值6,则AC+BC<6,与题意不符.
设点C的坐标为(x,0).∵AC+BC=10,∴[x-(-3)]+(x-3)=10.解得,x=5.∴点C的坐标为(5,0).第三种情况:点C在y轴上方.设点C的坐标为(0,y).∵AC+BC=10,点A(-3,0),B(3,0),∴AC=BC=5,32+y =52.解得,y=±4.∵点C在y轴上方,∴点C的坐标为(0,4).第四种情况:点C在y轴下方.设点C的坐标为(0,y).∵AC+BC=10,点A(-3,0),B(3,0),∴AC=BC=5,32+y =52.解得,y=±4.∵点C在y轴下方,∴点C的坐标为(0,-4).故答案为(-5,0),(5,0),(0,4),(0,-4).
三.解答题(60分)
21.(8分)已知a,b都是实数,设点P(a+2,),且满足3a=2+b,我们称点P为“梦之点”.
(1)判断点A(3,2)是否为“梦之点”,并说明理由.
(2)若点M(m﹣1,3m+2)是“梦之点”,请判断点M在第几象限,并说明理由.
解:(1)当A(3,2)时,a+2=3,,解得a=1,b=1,则3a=3,2+b=3,
所以3a=2+b,所以A(3,2),是“梦之点”;
(2)点M在第三象限,理由如下:∵点M(m﹣1,3m+2)是“梦之点”,∴a+2=m﹣1,,
∴a=m﹣3,b=6m+1,∴代入3a=2+b有3(m﹣3)=2+(6m+1),解得m=﹣4,∴m﹣1=﹣5,3m+2=﹣10,∴点M在第三象限.
22.(8分)在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”,例如,点P(1,4)的3级关联点”为Q(3×1+4,1+3×4)即Q(7,13),若点B的“2级关联点”是B(3,3).
(1)求点B的坐标;
(2)已知点M(m﹣1,2m)的“﹣3级关联点”N位于y轴上,求N的坐标.
解:∵点B的“2级关联点”是B'(3,3),∴,解得:,
则点B的坐标为(1,1);
(2)∵点M(m﹣1,2m)的“﹣3级关联点”N的坐标为(﹣m+3,﹣5m﹣1),且点N在y轴上,∴﹣m+3=0,解得m=3,则﹣5m﹣1=﹣16,∴点N坐标为(0,﹣16).
23、(8分)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.
解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)①如图①,当0<a≤3时,因为点P与点P1关于y轴对称,P(-a,0),所以P1(a,0).因为点P1与点P2关于直线x=3对称,设P2(x,0),可得=3,即x=6-a,所以P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.②如图②,当a>3时,因为点P与点P1关于y轴对称,P(-a,0),所以P1(a,0).因为点P1与点P2关于直线x=3对称,设P2(x,0),可得=3,即x=6-a,所以P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
综上所述,PP2的长为6.
24.(12分)已知点P(2m+4,m﹣1),请分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣4)点,且与y轴平行的直线上;
(3)点P到两坐标轴的距离相等.
解:(1)根据题意,得(m﹣1)﹣(2m+4)=3, 解之,得m=﹣8,∴2m+4=﹣12,m﹣1=﹣9,∴点P的坐标为(﹣12,﹣9) (2)根据题意,得2m+4=2, 解之,得m=﹣1,∴2m+4=2,m﹣1=﹣2,∴点P的坐标为(2,﹣2)(3)根据题意,得2m+4=m﹣1或2m+4+m﹣1=0,
解之,得m=﹣5或m=﹣1,∴2m+4=﹣6,m﹣1=﹣6或2m+4=2,m﹣1=﹣2,∴点P的坐标为(﹣6,﹣6)或(2,﹣2)
25.(12分)已知点M(3a-2,a+6).
(1)若点M在x轴上,求点M的坐标
(2)变式一:已知点M(3a-2,a+6),点N(2,5),且直线MN∥x轴,求点M的坐标.
(3)变式二:已知点M(3a-2,a+6),若点M到x轴、y轴的距离相等,求点M的坐标.
解:(1)∵点M在x轴上,∴yM=0,即a+6=0,解得a=-6.当a=-6时,3a-2=3×(-6)-2=-20,因此点M的坐标为(-20,0).
(2)变式一:∵直线MN∥x轴,∴点M与点N的纵坐标相等, 即a+6=5,解得a=-1.当a=-1时,3a-2=3×(-1)- 2=-5,因此点M的坐标为(-5,5).
(3)∵点M在x轴上,∴yM=0,即a+6=0,解得a=-6.当a=-6时,3a-2=3×(-6)-2=-20,因此点M的坐标为(-20,0).
变式二:∵点M到x轴、y轴的距离相等,∴|3a-2|=|a+6| ,去绝对值号得3a-2=a+6或3a-2+a+6=0,解得a=4或a=-1.当a=4时,3a-2=3×4-2=10,a+6=4+6=10,点M的坐标为(10,10);当a=-1时,3a-2=3×(-1)-2=-5,a+6=-1+6=5,点M的坐标为(-5,5).因此点M的坐标为(10,10)或(-5,5).
26.(12分)问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
解:【应用】:(1)AB的长度为|﹣1﹣2|=3.故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),∵CD=2,∴|0﹣m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,﹣2).故答案为:(1,2)或(1,﹣2).
【拓展】:(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.故答案为:=5.
(2)∵E(2,0),H(1,t),d(E,H)=3,∴|2﹣1|+|0﹣t|=3,解得:t=±2.
故答案为:2或﹣2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),∵三角形OPQ的面积为3,
∴|x|×3=3,解得:x=±2.当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8.故答案为:4或8.
(时间:100分钟 满分:120分)
一.选择题(共30分)
1.点P1(a﹣1,2024)和P2(2023,b﹣1)关于x轴对称,则(a+b)2021的值为( )
A.﹣1 B.1 C.0 D.无法确定
2.已知两点A(a,5),B(﹣1,b)且直线AB∥x轴,则( )
A.a可取任意实数,b=5 B.a=﹣1,b可取任意实数
C.a≠﹣1,b=5 D.a=﹣1,b≠5
3.在平面直角坐标系xOy中,过点P(﹣2,3)作PA⊥y轴,垂足为点A,那么PA的长为( )
A.2 B.3 C.5 D.
4.在平面直角坐标系中,将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是( )
A.(3,8) B.(1,8) C.(1,4) D.(3,4)
5.在平面直角坐标系中点P(﹣20,a)与点Q(b,13)关于y轴对称,则﹣a+b的值为( )
A.﹣33 B.33 C.﹣7 D.7
6、若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f (1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g(f(3,﹣4))的值为( )
A.(3,﹣4) B.(﹣3,4) C.(3,4) D.(﹣3,﹣4)
7.如图,在平面直角坐标系中,点A是x轴正半轴上的一个动点,点C是y轴正半轴上的点,BC⊥AC于点C.已知AC=16,BC=6.点B到原点的最大距离为( )
A.22 B.18 C.14 D.10
第7题图 第8题图 第9题图 第10题图
8.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( C )
A.2 B.3 C.4 D.5
9.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( )
A.2 B.3 C.4 D.5
10.如图,平面直角坐标系xOy中,点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°.在x轴上取一点P(m,0),过点P作直线l垂直于直线OA,将OB关于直线l的对称图形记为O′B′,当O′B′和过A点且平行于x轴的直线有交点时,m的取值范围为( )
A.m≥4 B.m≤6 C.4<m<6 D.4≤m≤6
二.填空题(共30分)
11.点A(3,﹣2)关于x轴对称的点的坐标是 .
12.点P(2,﹣3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P′的坐标是 .
13.在平面直角坐标系中,A,B,C三点的坐标分别是A(5,0),B(0,3),C(5,3),O为坐标原点,点E在线段BC上.若△AEO为等腰三角形,点E的坐标为_______________.
14.已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)的坐标为 .
15.在平面直角坐标系中,若A(x1,y1)、B(x2,y2),则AB=,若M(﹣4,1)、N(2,﹣1),则MN= .
16.已知点A在x轴的下方,且到x轴的距离为5,到y轴的距离为3,则点A的坐标为________.
17.已知点M(3,2)与点N(x,y)在同一条平行于x轴的直线上,且点N到y轴的距离为8,则点N的坐标为________.
18.如图,在平面直角坐标系中,第1次将边长为1个单位长度的正方形OABC绕点O逆时针旋转45°后,得到正方形OA1B1C1;第2次将正方形OA1B1C1绕点O逆时针旋转45°后,得到正方形OA2B2C2;……,按此规律,绕点O旋转得到正方形OA2 023B2 024C2 023,则点B2 024的坐标为 .
第18题图 第19题图
19.如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为 .
20.在平面直角坐标系中,已知点A(-3,0),B(3,0),点C在坐标轴上,且AC+BC=10,写出满足条件的所有点C的坐标:________.
三.解答题(60分)
21.(8分)已知a,b都是实数,设点P(a+2,),且满足3a=2+b,我们称点P为“梦之点”.
(1)判断点A(3,2)是否为“梦之点”,并说明理由.
(2)若点M(m﹣1,3m+2)是“梦之点”,请判断点M在第几象限,并说明理由.
22.(8分)在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”,例如,点P(1,4)的3级关联点”为Q(3×1+4,1+3×4)即Q(7,13),若点B的“2级关联点”是B(3,3).
(1)求点B的坐标;
(2)已知点M(m﹣1,2m)的“﹣3级关联点”N位于y轴上,求N的坐标.
23、(8分)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.
24.(12分)已知点P(2m+4,m﹣1),请分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣4)点,且与y轴平行的直线上;
(3)点P到两坐标轴的距离相等.
25.(12分)已知点M(3a-2,a+6).
(1)若点M在x轴上,求点M的坐标
(2)变式一:已知点M(3a-2,a+6),点N(2,5),且直线MN∥x轴,求点M的坐标.
(3)变式二:已知点M(3a-2,a+6),若点M到x轴、y轴的距离相等,求点M的坐标.
26.(12分)问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
教师样卷
一.选择题(共30分)
1.点P1(a﹣1,2024)和P2(2023,b﹣1)关于x轴对称,则(a+b)2021的值为( A )
A.﹣1 B.1 C.0 D.无法确定
2.已知两点A(a,5),B(﹣1,b)且直线AB∥x轴,则( C )
A.a可取任意实数,b=5 B.a=﹣1,b可取任意实数
C.a≠﹣1,b=5 D.a=﹣1,b≠5
3.在平面直角坐标系xOy中,过点P(﹣2,3)作PA⊥y轴,垂足为点A,那么PA的长为( A )
A.2 B.3 C.5 D.
4.在平面直角坐标系中,将点P(2,6)向上平移2个单位长度,再向左平移1个单位长度得到的点的坐标是( B )
A.(3,8) B.(1,8) C.(1,4) D.(3,4)
5.在平面直角坐标系中点P(﹣20,a)与点Q(b,13)关于y轴对称,则﹣a+b的值为( D )
A.﹣33 B.33 C.﹣7 D.7
解:∵在平面直角坐标系内点P(﹣20,a)与点Q(b,13)关于y轴对称,∴a=13,b=20,则﹣a+b=﹣13+20=7.故选:D.
6、若定义:f(a,b)=(﹣a,b),g(m,n)=(m,﹣n),例如f (1,2)=(﹣1,2),g(﹣4,﹣5)=(﹣4,5),则g(f(3,﹣4))的值为( B )
A.(3,﹣4) B.(﹣3,4) C.(3,4) D.(﹣3,﹣4)
解:g(f(3,﹣4))=g(﹣3,﹣4)=(﹣3,4),故选:B.
7.如图,在平面直角坐标系中,点A是x轴正半轴上的一个动点,点C是y轴正半轴上的点,BC⊥AC于点C.已知AC=16,BC=6.点B到原点的最大距离为( B )
A.22 B.18 C.14 D.10
解:取AC的中点D,连接OD,BD,OB,如图,∵D为AC的中点,∠AOC=90°,∴OD=CD=AC=8.∵∠ACB=90°,∴BD===10.当O,D,B三点不在一条直线上时,OB<OD+BD=8+10=18,当O,D,B三点在一条直线上时,OB=OD+BD=8+10=18,∴当O,D,B三点在一条直线上时,点B到原点的最大距离为18.故选:B.
8.定义:直线l1与l2相交于点O,对于平面内任意一点M,点M到直线l1、l2的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”,根据上述定义,“距离坐标”是(1,2)的点的个数是( C )
A.2 B.3 C.4 D.5
解:如图,∵到直线l1的距离是1的点在与直线l1平行且与l1的距离是1的两条平行线a1、a2上,到直线l2的距离是2的点在与直线l2平行且与l2的距离是2的两条平行线b1、b2上,∴“距离坐标”是(1,2)的点是M1、M2、M3、M4,一共4个.故选C.
9.如图,A,B的坐标为(2,0),(0,1),若将线段AB平移至A1B1,则a+b的值为( A )
A.2 B.3 C.4 D.5
解:由B点平移前后的纵坐标分别为1、2,可得B点向上平移了1个单位,由A点平移前后的横坐标分别是为2、3,可得A点向右平移了1个单位,由此得线段AB的平移的过程是:向上平移1个单位,再向右平移1个单位,所以点A、B均按此规律平移,由此可得a=0+1=1,b=0+1=1,故a+b=2.故选:A.
10.如图,平面直角坐标系xOy中,点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°.在x轴上取一点P(m,0),过点P作直线l垂直于直线OA,将OB关于直线l的对称图形记为O′B′,当O′B′和过A点且平行于x轴的直线有交点时,m的取值范围为( D )
A.m≥4 B.m≤6 C.4<m<6 D.4≤m≤6
解:如右图所示,当直线l垂直平分OA时,O′B′和过A点且平行于x轴的直线有交点,
∵点A在第一象限,B(2,0),∠AOB=60°,∠ABO=90°,∴∠BAO=30°,OB=2,
∴OA=4,∵直线l垂直平分OA,点P(m,0)是直线l与x轴的交点,∴OP=4,∴当m=4;作BB″∥OA,交过点A且平行于x轴的直线与B″,当直线l垂直平分BB″和过A点且平行于x轴的直线有交点,∵四边形OBB″O′是平行四边形,∴此时点P与x轴交点坐标为(6,0),由图可知,当OB关于直线l的对称图形为O′B′到O″B″的过程中点P符合题目中的要求,∴m的取值范围是4≤m≤6,故选:D.
二.填空题(共30分)
11.点A(3,﹣2)关于x轴对称的点的坐标是 (3,2) .
12.点P(2,﹣3)先向左平移4个单位长度,再向上平移1个单位长度,得到点P′的坐标是 (﹣2,﹣2) .
13.在平面直角坐标系中,A,B,C三点的坐标分别是A(5,0),B(0,3),C(5,3),O为坐标原点,点E在线段BC上.若△AEO为等腰三角形,点E的坐标为__(1,3),(2.5,3) ,(4,3)_____________.
解: 画出图形如解图.①若A为顶角顶点,则AE=AO,故点E(1,3).②若E为顶角顶点,则EO=EA,故点E(2.5,3).③若O为顶角顶点,则OE=OA,故点E(4,3).
14.已知A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,则C(a,b)的坐标为 (5,﹣3) .
解:∵A(a﹣5,2b﹣1)在y轴上,B(3a+2,b+3)在x轴上,∴a﹣5=0,b+3=0,解得:a=5,b=﹣3,∴C(a,b)的坐标为:(5,﹣3).
15.在平面直角坐标系中,若A(x1,y1)、B(x2,y2),则AB=,若M(﹣4,1)、N(2,﹣1),则MN= 2 .
解:∵M(﹣4,1)、N(2,﹣1),∴MN==2,故答案为:2.
16.已知点A在x轴的下方,且到x轴的距离为5,到y轴的距离为3,则点A的坐标为__(3,﹣5)或(﹣3,﹣5) ______.
解:∵点A在x轴的下方,且到x轴的距离为5,到y轴的距离为3,∴点A的纵坐标为:﹣5,横坐标为:±3,故点A的坐标为:(3,﹣5)或(﹣3,﹣5).
故答案为:(3,﹣5)或(﹣3,﹣5).
17.已知点M(3,2)与点N(x,y)在同一条平行于x轴的直线上,且点N到y轴的距离为8,则点N的坐标为_(8,2)或(-8,2)_______.
解:由点M(3,2)与点N(x,y)在同一条平行于x轴的直线上可得:y=2;由点N到y轴的距离为8可得x=±8,所以点N的坐标为(8,2)或(-8,2).
故答案为(8,2)或(-8,2).
18.如图,在平面直角坐标系中,第1次将边长为1个单位长度的正方形OABC绕点O逆时针旋转45°后,得到正方形OA1B1C1;第2次将正方形OA1B1C1绕点O逆时针旋转45°后,得到正方形OA2B2C2;……,按此规律,绕点O旋转得到正方形OA2 023B2 024C2 023,则点B2 024的坐标为 (1,1).
解:∵四边形OABC是正方形,OA=1,∴B(1,1),如图,连结OB,根据勾股定理可得OB=,
由旋转可得OB=OB1=OB2=…=OB2 020=,∠AOB=∠BOB1=∠B1OB2=…=∠B2 023OB2 024=45°,
∴B1(0,),B2(-1,1),B3(-,0),B4(-1,-1),B5(0,-),B6(1,-1),B7(,0),B8(1,1),B9(0,),……,∴8次一循环,∵2 024÷8=253,∴点B2 024的坐标为(1,1).
第18题图 第19题图
19.如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为 ﹣()2023 .
解:∵A1(1,0),A2[0,()1],A3[﹣()2,0].A4[0,﹣()3],A5[()4,0]…,∴序号除以4整除的话在y轴的负半轴上,余数是1在x轴的正半轴上,余数是2在y轴的正半轴上,余数是3在x轴的负半轴上,∵2024÷4=506,∴A2024在y轴的负半轴上,纵坐标为﹣()2023.故答案为﹣()2023.
20.在平面直角坐标系中,已知点A(-3,0),B(3,0),点C在坐标轴上,且AC+BC=10,写出满足条件的所有点C的坐标:___ (-5,0),(5,0),(0,4),(0,-4) _____.
解:第一种情况:当点C在x轴左半轴时,点C在点A的左侧. 若C在点A的右侧,只能当A与C重合时取最大值6,则AC+BC<6,与题意不符.设点C的坐标为(x,0).∵AC+BC=10,点A(-3,0),B(3,0),∴(-3-x)+(3-x)=10.解得,x=-5.∴点C的坐标为(-5,0),点A(-3,0),B(3,0),第二种情况:当点C在x轴左半轴时,点C在点B的右侧.若C在点B的左侧,只能当与B,C重合时取最大值6,则AC+BC<6,与题意不符.
设点C的坐标为(x,0).∵AC+BC=10,∴[x-(-3)]+(x-3)=10.解得,x=5.∴点C的坐标为(5,0).第三种情况:点C在y轴上方.设点C的坐标为(0,y).∵AC+BC=10,点A(-3,0),B(3,0),∴AC=BC=5,32+y =52.解得,y=±4.∵点C在y轴上方,∴点C的坐标为(0,4).第四种情况:点C在y轴下方.设点C的坐标为(0,y).∵AC+BC=10,点A(-3,0),B(3,0),∴AC=BC=5,32+y =52.解得,y=±4.∵点C在y轴下方,∴点C的坐标为(0,-4).故答案为(-5,0),(5,0),(0,4),(0,-4).
三.解答题(60分)
21.(8分)已知a,b都是实数,设点P(a+2,),且满足3a=2+b,我们称点P为“梦之点”.
(1)判断点A(3,2)是否为“梦之点”,并说明理由.
(2)若点M(m﹣1,3m+2)是“梦之点”,请判断点M在第几象限,并说明理由.
解:(1)当A(3,2)时,a+2=3,,解得a=1,b=1,则3a=3,2+b=3,
所以3a=2+b,所以A(3,2),是“梦之点”;
(2)点M在第三象限,理由如下:∵点M(m﹣1,3m+2)是“梦之点”,∴a+2=m﹣1,,
∴a=m﹣3,b=6m+1,∴代入3a=2+b有3(m﹣3)=2+(6m+1),解得m=﹣4,∴m﹣1=﹣5,3m+2=﹣10,∴点M在第三象限.
22.(8分)在平面直角坐标系中,对于点P(x,y),若点Q的坐标为(ax+y,x+ay),其中a为常数,则称点Q是点P的“a级关联点”,例如,点P(1,4)的3级关联点”为Q(3×1+4,1+3×4)即Q(7,13),若点B的“2级关联点”是B(3,3).
(1)求点B的坐标;
(2)已知点M(m﹣1,2m)的“﹣3级关联点”N位于y轴上,求N的坐标.
解:∵点B的“2级关联点”是B'(3,3),∴,解得:,
则点B的坐标为(1,1);
(2)∵点M(m﹣1,2m)的“﹣3级关联点”N的坐标为(﹣m+3,﹣5m﹣1),且点N在y轴上,∴﹣m+3=0,解得m=3,则﹣5m﹣1=﹣16,∴点N坐标为(0,﹣16).
23、(8分)如图,在平面直角坐标系中,直线l过点M(3,0),且平行于y轴.(1)如果△ABC三个顶点的坐标分别是A(﹣2,0),B(﹣1,0),C(﹣1,2),△ABC关于y轴的对称图形是△A1B1C1,△A1B1C1关于直线l的对称图形是△A2B2C2,写出△A2B2C2的三个顶点的坐标;(2)如果点P的坐标是(﹣a,0),其中0<a<3,点P关于y轴的对称点是P1,点P1关于直线l的对称点是P2,求PP2的长.
解:(1)△A2B2C2的三个顶点的坐标分别是A2(4,0),B2(5,0),C2(5,2).
(2)①如图①,当0<a≤3时,因为点P与点P1关于y轴对称,P(-a,0),所以P1(a,0).因为点P1与点P2关于直线x=3对称,设P2(x,0),可得=3,即x=6-a,所以P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.②如图②,当a>3时,因为点P与点P1关于y轴对称,P(-a,0),所以P1(a,0).因为点P1与点P2关于直线x=3对称,设P2(x,0),可得=3,即x=6-a,所以P2(6-a,0),则PP2=6-a-(-a)=6-a+a=6.
综上所述,PP2的长为6.
24.(12分)已知点P(2m+4,m﹣1),请分别根据下列条件,求出点P的坐标.
(1)点P的纵坐标比横坐标大3;
(2)点P在过A(2,﹣4)点,且与y轴平行的直线上;
(3)点P到两坐标轴的距离相等.
解:(1)根据题意,得(m﹣1)﹣(2m+4)=3, 解之,得m=﹣8,∴2m+4=﹣12,m﹣1=﹣9,∴点P的坐标为(﹣12,﹣9) (2)根据题意,得2m+4=2, 解之,得m=﹣1,∴2m+4=2,m﹣1=﹣2,∴点P的坐标为(2,﹣2)(3)根据题意,得2m+4=m﹣1或2m+4+m﹣1=0,
解之,得m=﹣5或m=﹣1,∴2m+4=﹣6,m﹣1=﹣6或2m+4=2,m﹣1=﹣2,∴点P的坐标为(﹣6,﹣6)或(2,﹣2)
25.(12分)已知点M(3a-2,a+6).
(1)若点M在x轴上,求点M的坐标
(2)变式一:已知点M(3a-2,a+6),点N(2,5),且直线MN∥x轴,求点M的坐标.
(3)变式二:已知点M(3a-2,a+6),若点M到x轴、y轴的距离相等,求点M的坐标.
解:(1)∵点M在x轴上,∴yM=0,即a+6=0,解得a=-6.当a=-6时,3a-2=3×(-6)-2=-20,因此点M的坐标为(-20,0).
(2)变式一:∵直线MN∥x轴,∴点M与点N的纵坐标相等, 即a+6=5,解得a=-1.当a=-1时,3a-2=3×(-1)- 2=-5,因此点M的坐标为(-5,5).
(3)∵点M在x轴上,∴yM=0,即a+6=0,解得a=-6.当a=-6时,3a-2=3×(-6)-2=-20,因此点M的坐标为(-20,0).
变式二:∵点M到x轴、y轴的距离相等,∴|3a-2|=|a+6| ,去绝对值号得3a-2=a+6或3a-2+a+6=0,解得a=4或a=-1.当a=4时,3a-2=3×4-2=10,a+6=4+6=10,点M的坐标为(10,10);当a=-1时,3a-2=3×(-1)-2=-5,a+6=-1+6=5,点M的坐标为(-5,5).因此点M的坐标为(10,10)或(-5,5).
26.(12分)问题情境:
在平面直角坐标系xOy中有不重合的两点A(x1,y1)和点B(x2,y2),小明在学习中发现,若x1=x2,则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2,则AB∥x轴,且线段AB的长度为|x1﹣x2|;
【应用】:
(1)若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为 .
(2)若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为 .
【拓展】:
我们规定:平面直角坐标系中任意不重合的两点M(x1,y1),N(x2,y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
(1)如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F) ;
(2)如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t= .
(3)如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)= .
解:【应用】:(1)AB的长度为|﹣1﹣2|=3.故答案为:3.
(2)由CD∥y轴,可设点D的坐标为(1,m),∵CD=2,∴|0﹣m|=2,解得:m=±2,
∴点D的坐标为(1,2)或(1,﹣2).故答案为:(1,2)或(1,﹣2).
【拓展】:(1)d(E,F)=|2﹣(﹣1)|+|0﹣(﹣2)|=5.故答案为:=5.
(2)∵E(2,0),H(1,t),d(E,H)=3,∴|2﹣1|+|0﹣t|=3,解得:t=±2.
故答案为:2或﹣2.
(3)由点Q在x轴上,可设点Q的坐标为(x,0),∵三角形OPQ的面积为3,
∴|x|×3=3,解得:x=±2.当点Q的坐标为(2,0)时,d(P,Q)=|3﹣2|+|3﹣0|=4;当点Q的坐标为(﹣2,0)时,d(P,Q)=|3﹣(﹣2)|+|3﹣0|=8.故答案为:4或8.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
