教科版高中物理必修二第三章 万有引力定律第1节《天体运动》参考课件 (共30张PPT)
文档属性
| 名称 | 教科版高中物理必修二第三章 万有引力定律第1节《天体运动》参考课件 (共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 641.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2015-05-06 11:21:53 | ||
图片预览








文档简介
课件30张PPT。第1节 天体运动 核心要点突破课堂互动讲练第1节 课前自主学案课标定位课标定位应用:1.运用开普勒定律解释有关现象.
2.对行星运动运用圆周运动知识求解.
理解:1.描述行星运动的规律——开普勒三定律.
2.开普勒定律的近似处理.
认识:1.地心说和日心说的基本内容.
2.所有行星绕太阳运动的轨道均为椭圆,太阳处在椭圆的一个焦点上.课前自主学案一、日心说
1.地心说
托勒密认为,_____是宇宙的中心,是静止不动的,其他天体围绕_______转动.
2.日心说
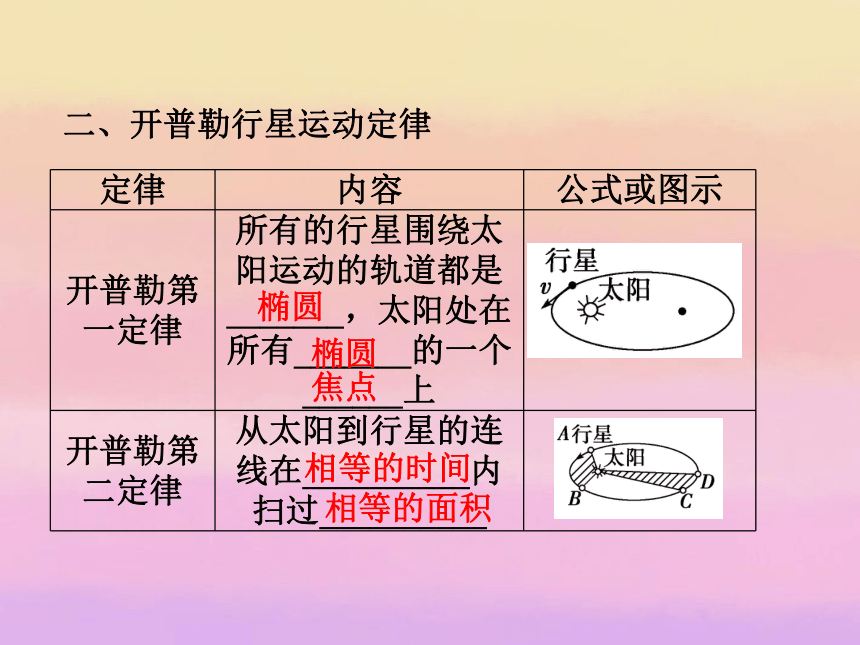
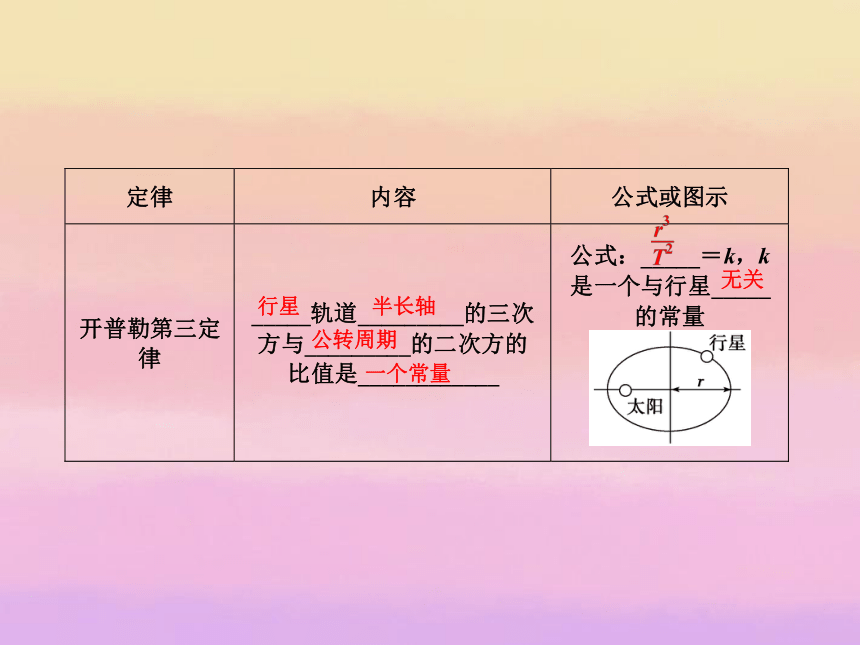
哥白尼认为,地球和别的行星一样,围绕_____运动,____固定在这个体系的中心.地球地球太阳太阳二、开普勒行星运动定律椭圆椭圆焦点相等的时间相等的面积行星半长轴公转周期一个常量无关思考感悟
行星绕太阳在椭圆轨道上运行,行星距太阳较近处与距太阳较远处相比较,运动速率何处较大?
提示:由开普勒第二定律可知,由于在相等的时间内,行星与太阳的连线扫过相等的面积,显然相距较近时相等时间内经过的弧长必须较长,因此运动速率较大.核心要点突破一、对开普勒行星运动定律的认识
1.从空间分布认识
图3-1-1行星的轨道都是椭圆,所有椭圆有一个共同的焦点,太阳就在此焦点上.
因此第一定律又叫椭圆轨道定律,如图3-1-1所示.
意义:第一定律告诉我们,尽管各行星的轨道大小不同,但它们的共同规律是:所有行星都沿椭圆轨道绕太阳运动,太阳则位于所有椭圆的一个公共焦点上.否定了行星圆形轨道的说法,建立了正确的轨道理论,给出了太阳准确的位置.2.从速度大小认识
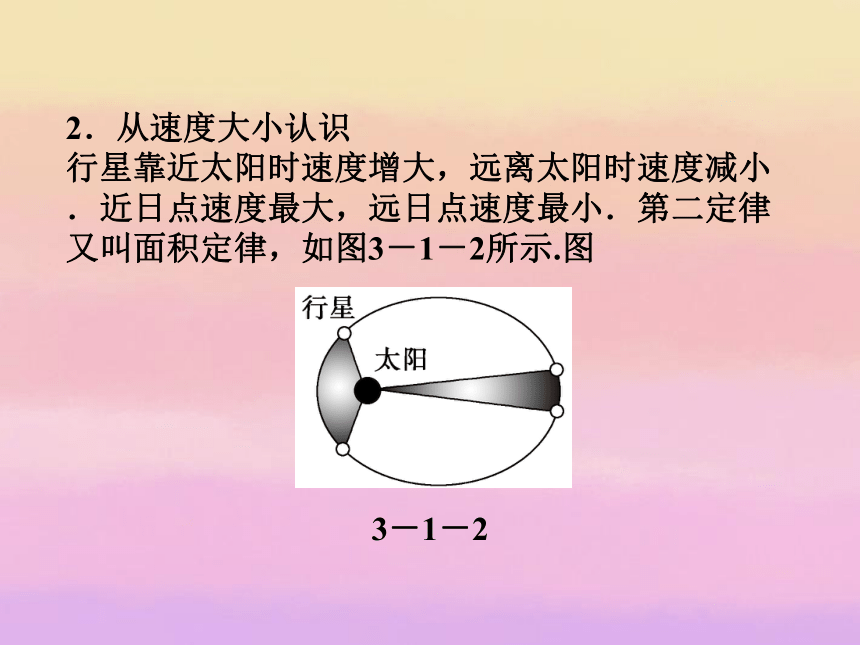
行星靠近太阳时速度增大,远离太阳时速度减小.近日点速度最大,远日点速度最小.第二定律又叫面积定律,如图3-1-2所示.图
3-1-2特别提醒:(1)行星绕太阳的运动不是匀速圆周运动,所以行星的速度方向并不总是垂直于行星和太阳的连线,但行星绕太阳运动一周的时间仍为一个周期,此周期不能用匀速圆周运动求解,而应根据开普勒定律对不同运动应用其相应的运动规律去判断和求解;做椭圆运动的卫星可用此规律求解.(2)在同一天体系统中,如果已知某一“行星”的公转周期而求其轨道半径时,可通过另一已知轨道半径和周期的“行星”利用开普勒第三定律解答.三、天体运动的规律及分析方法
1.天体虽做椭圆运动,但它们的轨道一般接近圆.中学阶段我们在处理天体运动问题时,为简化运算,一般把天体的运动当做圆周运动来研究,并且把它们视为做匀速圆周运动,椭圆的半长轴即为圆半径.课堂互动讲练 关于行星绕太阳运动的下列说法中正确的是( )
A.所有行星都在同一椭圆轨道上绕太阳运动
B.行星绕太阳运动时太阳位于行星轨道的中心处
C.离太阳越近的行星的运动周期越长
D.所有行星的轨道半长轴的三次方跟公转周期的二次方的比值都相等
【思路点拨】 太阳系中行星运动的轨道、速率及周期遵循开普勒三定律.【精讲精析】 不同的行星,有不同的椭圆轨道,太阳在椭圆轨道的一个焦点上,故A、B错误;由开普勒第三定律知,所有行星的轨道半长轴的三次方跟公转周期的二次方的比值都相等,半长轴越大,其公转周期越长,故C错误,D正确.
【答案】 D【方法总结】 (1)行星绕太阳运行的轨道为椭圆轨道,太阳在所有椭圆轨道的公共焦点上.
(2)行星运动定律虽是由太阳系中行星的运动总结出来的,但该定律同样适用于其他天体系统.
图3-1-4
飞船沿半径为R的圆周轨道绕地球运动,其周期为T.如果飞船要返回地面,可在轨道上的某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的椭圆轨道运动,椭圆和地球表面在B点相切,如图3-1-4所示. 如果地球半径为R0,求飞船由A点到B点所需要的时间.【思路点拨】 开普勒第三定律虽然是根据行星绕太阳的运动总结出来的,但也适用于卫星、飞船等绕行星的运动.飞船绕地球做圆周运动的半长轴即为圆的半径.【方法总结】 涉及与椭圆轨道运动周期相关的问题,常用开普勒第三定律求解,但该定律只能用在同一中心天体的两星体之间.变式训练2 天文学家观察到哈雷彗星的转动周期是75年,离太阳最近的距离是8.9×1010 m,离太阳最远的距离不能被测出.试根据开普勒定律估算这个最远距离,太阳系的开普勒常数k=3.354×1018 m3/s2.
2.对行星运动运用圆周运动知识求解.
理解:1.描述行星运动的规律——开普勒三定律.
2.开普勒定律的近似处理.
认识:1.地心说和日心说的基本内容.
2.所有行星绕太阳运动的轨道均为椭圆,太阳处在椭圆的一个焦点上.课前自主学案一、日心说
1.地心说
托勒密认为,_____是宇宙的中心,是静止不动的,其他天体围绕_______转动.
2.日心说
哥白尼认为,地球和别的行星一样,围绕_____运动,____固定在这个体系的中心.地球地球太阳太阳二、开普勒行星运动定律椭圆椭圆焦点相等的时间相等的面积行星半长轴公转周期一个常量无关思考感悟
行星绕太阳在椭圆轨道上运行,行星距太阳较近处与距太阳较远处相比较,运动速率何处较大?
提示:由开普勒第二定律可知,由于在相等的时间内,行星与太阳的连线扫过相等的面积,显然相距较近时相等时间内经过的弧长必须较长,因此运动速率较大.核心要点突破一、对开普勒行星运动定律的认识
1.从空间分布认识
图3-1-1行星的轨道都是椭圆,所有椭圆有一个共同的焦点,太阳就在此焦点上.
因此第一定律又叫椭圆轨道定律,如图3-1-1所示.
意义:第一定律告诉我们,尽管各行星的轨道大小不同,但它们的共同规律是:所有行星都沿椭圆轨道绕太阳运动,太阳则位于所有椭圆的一个公共焦点上.否定了行星圆形轨道的说法,建立了正确的轨道理论,给出了太阳准确的位置.2.从速度大小认识
行星靠近太阳时速度增大,远离太阳时速度减小.近日点速度最大,远日点速度最小.第二定律又叫面积定律,如图3-1-2所示.图
3-1-2特别提醒:(1)行星绕太阳的运动不是匀速圆周运动,所以行星的速度方向并不总是垂直于行星和太阳的连线,但行星绕太阳运动一周的时间仍为一个周期,此周期不能用匀速圆周运动求解,而应根据开普勒定律对不同运动应用其相应的运动规律去判断和求解;做椭圆运动的卫星可用此规律求解.(2)在同一天体系统中,如果已知某一“行星”的公转周期而求其轨道半径时,可通过另一已知轨道半径和周期的“行星”利用开普勒第三定律解答.三、天体运动的规律及分析方法
1.天体虽做椭圆运动,但它们的轨道一般接近圆.中学阶段我们在处理天体运动问题时,为简化运算,一般把天体的运动当做圆周运动来研究,并且把它们视为做匀速圆周运动,椭圆的半长轴即为圆半径.课堂互动讲练 关于行星绕太阳运动的下列说法中正确的是( )
A.所有行星都在同一椭圆轨道上绕太阳运动
B.行星绕太阳运动时太阳位于行星轨道的中心处
C.离太阳越近的行星的运动周期越长
D.所有行星的轨道半长轴的三次方跟公转周期的二次方的比值都相等
【思路点拨】 太阳系中行星运动的轨道、速率及周期遵循开普勒三定律.【精讲精析】 不同的行星,有不同的椭圆轨道,太阳在椭圆轨道的一个焦点上,故A、B错误;由开普勒第三定律知,所有行星的轨道半长轴的三次方跟公转周期的二次方的比值都相等,半长轴越大,其公转周期越长,故C错误,D正确.
【答案】 D【方法总结】 (1)行星绕太阳运行的轨道为椭圆轨道,太阳在所有椭圆轨道的公共焦点上.
(2)行星运动定律虽是由太阳系中行星的运动总结出来的,但该定律同样适用于其他天体系统.
图3-1-4
飞船沿半径为R的圆周轨道绕地球运动,其周期为T.如果飞船要返回地面,可在轨道上的某一点A处,将速率降低到适当数值,从而使飞船沿着以地心为焦点的椭圆轨道运动,椭圆和地球表面在B点相切,如图3-1-4所示. 如果地球半径为R0,求飞船由A点到B点所需要的时间.【思路点拨】 开普勒第三定律虽然是根据行星绕太阳的运动总结出来的,但也适用于卫星、飞船等绕行星的运动.飞船绕地球做圆周运动的半长轴即为圆的半径.【方法总结】 涉及与椭圆轨道运动周期相关的问题,常用开普勒第三定律求解,但该定律只能用在同一中心天体的两星体之间.变式训练2 天文学家观察到哈雷彗星的转动周期是75年,离太阳最近的距离是8.9×1010 m,离太阳最远的距离不能被测出.试根据开普勒定律估算这个最远距离,太阳系的开普勒常数k=3.354×1018 m3/s2.
