用样本估计总体

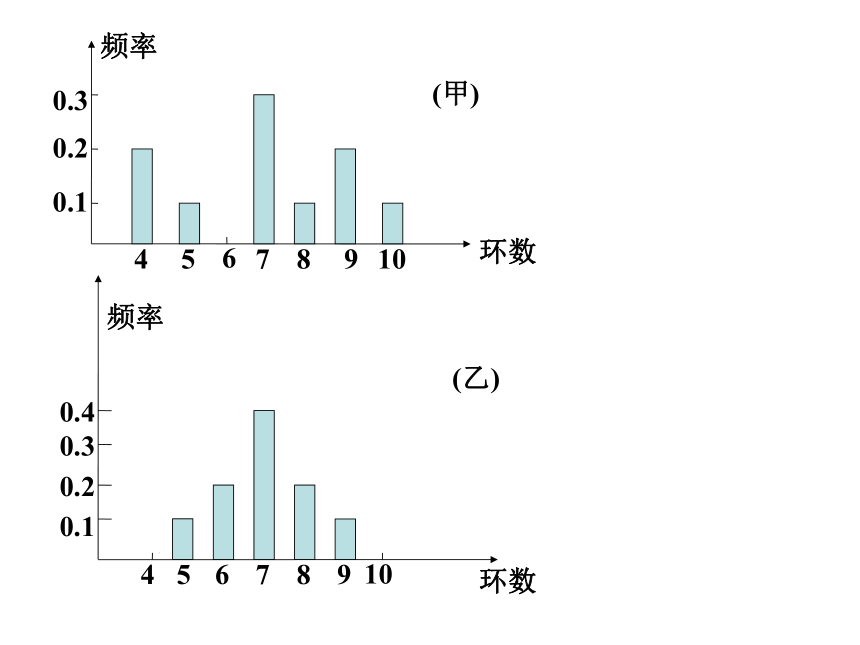
课件13张PPT。2.2.2 用样本的数字特征估计总体的数字特征标准差　 平均数向我们提供了样本数据的重要信息,但是平均有时也会使我们作出对总体的片面判断．因为这个平均数掩盖了一些极端的情况，而这些极端情况显然是不能忽的．因此，只有平均数还难以概括样本数据的实际状态． 如：有两位射击运动员在一次射击测试中各射靶10次，每次命中的环数如下：甲：７　８　７　９　５　４　９　１０　７　４乙：９　５　７　８　７　６　８　 ６　 ７　 ７如果你是教练,你应当如何对这次射击作出评价?如果看两人本次射击的平均成绩,由于 两人射击 的平均成绩是一样的.那么两个人的水平就没有什么差异吗?
45678910环数频率0.10.20.3(甲)456789100.10.20.30.4环数频率(乙)直观上看,还是有差异的.如:甲成绩比较分散,乙成绩相对集中(如图示).因此,我们还需要从另外的角度来考察这两组数据.例如:在作统计图,表时提到过的极差.
甲的环数极差=10-4=6
乙的环数极差=9-5=4.
它们在一定程度上表明了样本数据的分散程度,与平均数一起,可以给我们许多关于样本数据的信息.显然,极差对极端值非常敏感,注意到这一点,我们可以得到一种“去掉一个最高分,去掉一个最低分”的统计策略.考察样本数据的分散程度的大小，最常用的统计量是标准差．
标准差是样本平均数的一种平均距离，一般用s表示．所谓“平均距离”，其含义可作如下理解：假设样本数据是 , 表示这组数据的平均数,则 到 的距离是：于是样本数据 到 的平均距离是：由于上式含有绝对值，运算不太方便，因此，通常改用如下公式来计算标准差．考虑一个容量为2的样本: ,其样本的标准差为显然,标准差越大，则s 越大，数据的离散程度越大；标准差越小，数据的离散程度越小.例题1:画出下列四组样本数据的直方图,说明它们的异同点.(1) 5, 5, 5, 5, 5, 5, 5, 5, 5;(2) 4, 4, 4, 5 , 5, 5, 6, 6, 6;(3) 3 , 3 , 4 , 4 , 5, 6 , 6, 7 , 7;(4) 2 , 2 , 2 , 2, 5 , 8 , 8 , 8 , 8 ;解:四组样本数据的直方图是:0.51.012345678频率o0.51.0S=1.49(2)频率o12345678S=0.82频率o123456780.51.0S=2.83频率o123456780.51.0S=0.00(1)(3)(4)四组数据的平均数都是5.0,标准差分别是0.00,0.82,
1.49，2.83。虽然它们有相同的平均数,但是它们有不同的标准差,说明数据的分散程度是不一样的.例2 、甲乙两人同时生产内径为25.40mm的一种零件.为了对两人的生产质量进行评比,从他们生产的零件中各抽出20件,量得其内径尺寸如下(单位:mm)甲 25.46, 25.32, 25.45, 25.39, 25.36
25.34, 25.42, 25.45, 25.38, 25.42
25.39, 25.43, 25.39, 25.40, 25.44
25.40, 25.42, 25.35, 25.41, 25.39乙 25.40, 25.43, 25.44, 25.48, 25.48
25.47, 25.49, 25.49, 25.36, 25.34
25.33, 25.43, 25.43, 25.32, 25.47
25.31, 25.32, 25.32, 25.32, 25.48 从生产的零件内径的尺寸看,谁生产的质量较高?分析:由于零件的生产标准已经给出(内径25.40mm),生产质量可以从两个角度来衡量.
（1）各自的平均数与内径标准尺寸25.40mm的差异大时质量低,差异小时质量高;
（2）平均数与标准尺寸很接近时, 标准差小的时候质量高,标准差大的时候质量低.解:用计算器计算可得: ，因此甲生产的零件内径比乙的稳定程度要高得多。于是可以作出判断，甲生产的零件的质量比乙的高一些。 从样本平均数看,甲生产的零件内径比乙生产的更接近内径标准(25.40mm),但是差异很小；所以必须再从样本标准差看，标准差还可以用于对样本数据的另外一种解释.例如,在关于居民月均用水量的例子中,平均数标准差s=0.868 ,将有标准差的其他作用与表现形式