山东省济宁市济宁一中2014-2015学年高一下学期期中考试数学试题
文档属性
| 名称 | 山东省济宁市济宁一中2014-2015学年高一下学期期中考试数学试题 |  | |
| 格式 | zip | ||
| 文件大小 | 199.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-05-06 12:32:24 | ||
图片预览


文档简介
济宁一中高一下学期数学试题
出题人:张艳红 审题人:张岩
第I卷 选择题(共50分)
一. 选择题(本大题共10道小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母填在题后的括号内。)
1.已知角的终边过点,则的值为 ( )
A. B. C. D.
2.下列向量组中能作为表示它们所在平面内所有向量的基底的是 ( )
A. B.
C. D.
3.已知,则 ( )
A. B. C. D.
4. 已知向量满足,则向量与的夹角为( )
A.; B.; C.; D.
5.函数值的大小关系是 ( )
A. B .
C . D.
6. 已知向量,,若与的夹角为锐角,则实数的取值范围为( )
A. B. C. D.
7. 要得到的图象只需将y=3sin2x的图象 ( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
8. 在平行四边形ABCD中, AD = 1, , E为CD的中点. 若, 则AB的长为 ( )
A. B.1 C. D.2
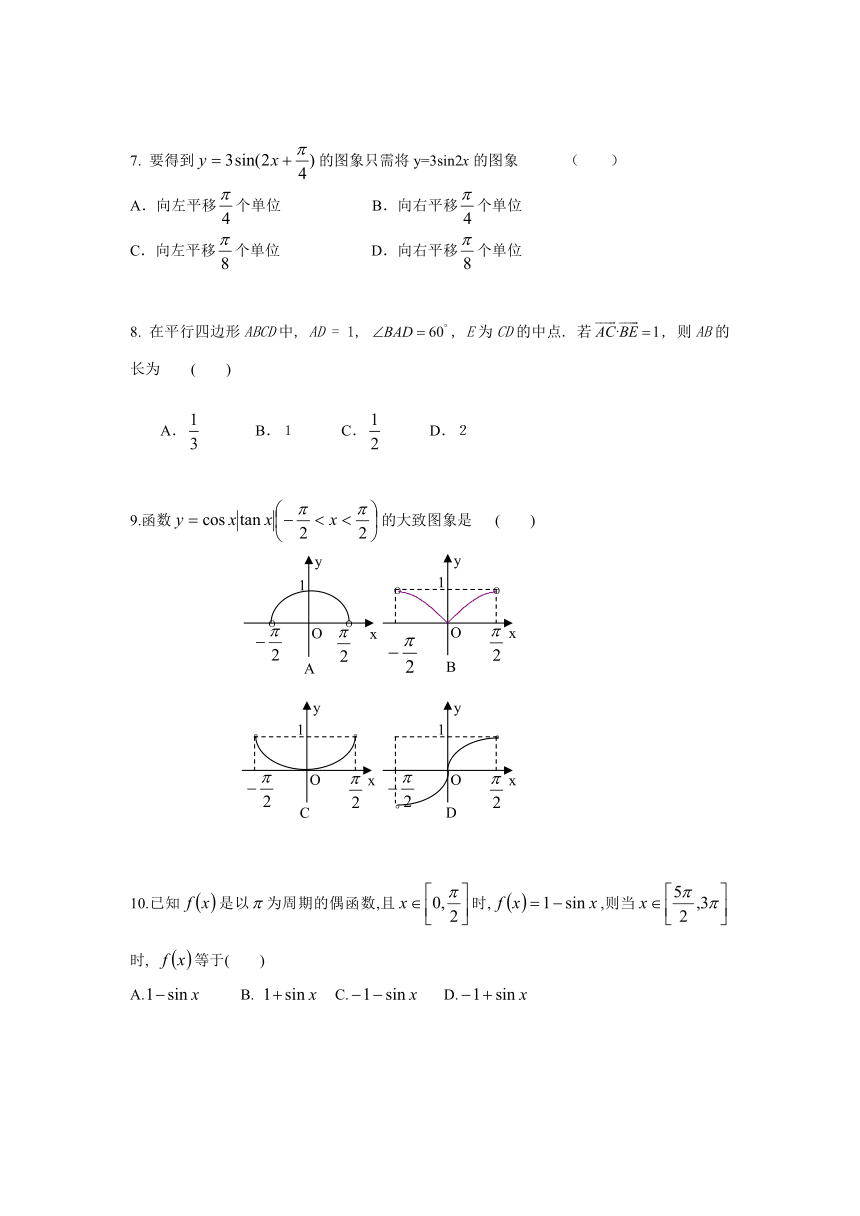
9.函数的大致图象是 ( )
10.已知是以为周期的偶函数,且时,,则当时, 等于( )
A. B. C. D.
第II卷 非选择题(共100分)
二.填空题(本大题共5道小题,每小题5分,共25分。把答案填在题中的横线上。)
11. 已知向量,则与向量共线的单位向量为
12 ( http: / / www. / wxc / ) 已知扇形的圆心角为,半径为3,则扇形的周长为
13. 已知 , ,则在方向上的投影为
14.定义运算 ,如:,则函数的值域为__________.
15.给出下列命题,其中正确命题的序号是________________________
① ②函数是偶函数
③若,则 ④是函数的一条对称轴方程
⑤若是第一象限的角,且,则
⑥函数的最大值为
三.解答题(本大题共6道小题,共75分。解答应写出文字说明或演算步骤。)
16. (本小题满分12分)
(1.)化简
(2.)已知,求
17. (本小题满分12分)
已知向量,= 。
⑴求与;
(2)当为何值时,向量与垂直?
(3)当为何值时,向量与平行?并确定此时它们是同向还是反向?
18.(本小题满分12分)
函数()的部分图象如图所示,
(1)求函数的解析式; (2)解不等式
19. (本小题满分12分)
某人在静水中游泳,速度为4公里/小时,他在水流速度为4公里/小时的河中游泳.
(1)若他垂直游向河对岸,则他实际沿什么方向前进?实际前进的速度为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度为多少?
20. (本小题满分13分)
已知向量,,
(1)求函数的单调减区间;
(2)若函数的图象上各点纵坐标不变,横坐标缩短为原来的得到函数的图象,试求函数在的值域。
21(本小题满分14分)
在平面直角坐标系中,已知向量又点.
(1)若,且为坐标原点),求向量;
(2)若向量与向量共线,当,且取最大值4时,求.
济宁一中高一下学期数学试题参考答案
一.选择题:CDDCA BCDBA
二.填空题:11. , 12. 13. 14. 15. ②⑥
三.解答题:
16.解:(1.) 原式=
===1……………………………….6分
(2.)由得
则=
=== …………………………………………………………12分
17. 解:(1),
……………………………………………………4分
(2),
向量与垂直,
解得,
当时,向量与垂直……………………………………………8分
(3)向量与平行,
解得,此时
时,向量与共线同向…………………………………………12分
18. 解:由图可知,,,
将点代入得,
,又,
…………………………………………………………6分
(2)由得,
,
不等式的解集为……………………12分
19. 解:(1)如图①,设人游泳的速度为,水流的速度为,以、为邻边作OACB,则此人的实际速度为
图① 图②
在Rt△ACO中,由勾股定理知||=8 且∠COA=60°,
故此人沿与河岸成60°的夹角顺着水流的方向前进,速度大小为8公里/小时. ……………………………………………………………………………………………6分
(2)如图②,设此人的实际速度为,水流速度为,则游速为,在Rt△AOD中,.
故此人沿与河岸成的夹角逆着水流方向前进,实际前进的速度大小为4公里/小时. ……………………………………………………………12分
20. 解:(1)=,
令得
函数的单调减区间为.………………………………6分
(2)由题意知,
,,
,
函数在的值域为………………………………………………13分
21解:(1)可得,∵,∴,
得.则,又.
∴,解得,
当时,;当时,.
∴或.……………………………………………………………6分
(2)∵向量与向量共线,∴
∴,
.
∵,∴,故当时,取最大值,有,得.
这时,,,,得,则.
∴.……………………………………………………………14分
o
o
x
y
O
1
x
y
O
1
o
o
x
y
O
1
°
°
x
y
O
1
°
°
A
B
C
D
出题人:张艳红 审题人:张岩
第I卷 选择题(共50分)
一. 选择题(本大题共10道小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母填在题后的括号内。)
1.已知角的终边过点,则的值为 ( )
A. B. C. D.
2.下列向量组中能作为表示它们所在平面内所有向量的基底的是 ( )
A. B.
C. D.
3.已知,则 ( )
A. B. C. D.
4. 已知向量满足,则向量与的夹角为( )
A.; B.; C.; D.
5.函数值的大小关系是 ( )
A. B .
C . D.
6. 已知向量,,若与的夹角为锐角,则实数的取值范围为( )
A. B. C. D.
7. 要得到的图象只需将y=3sin2x的图象 ( )
A.向左平移个单位 B.向右平移个单位
C.向左平移个单位 D.向右平移个单位
8. 在平行四边形ABCD中, AD = 1, , E为CD的中点. 若, 则AB的长为 ( )
A. B.1 C. D.2
9.函数的大致图象是 ( )
10.已知是以为周期的偶函数,且时,,则当时, 等于( )
A. B. C. D.
第II卷 非选择题(共100分)
二.填空题(本大题共5道小题,每小题5分,共25分。把答案填在题中的横线上。)
11. 已知向量,则与向量共线的单位向量为
12 ( http: / / www. / wxc / ) 已知扇形的圆心角为,半径为3,则扇形的周长为
13. 已知 , ,则在方向上的投影为
14.定义运算 ,如:,则函数的值域为__________.
15.给出下列命题,其中正确命题的序号是________________________
① ②函数是偶函数
③若,则 ④是函数的一条对称轴方程
⑤若是第一象限的角,且,则
⑥函数的最大值为
三.解答题(本大题共6道小题,共75分。解答应写出文字说明或演算步骤。)
16. (本小题满分12分)
(1.)化简
(2.)已知,求
17. (本小题满分12分)
已知向量,= 。
⑴求与;
(2)当为何值时,向量与垂直?
(3)当为何值时,向量与平行?并确定此时它们是同向还是反向?
18.(本小题满分12分)
函数()的部分图象如图所示,
(1)求函数的解析式; (2)解不等式
19. (本小题满分12分)
某人在静水中游泳,速度为4公里/小时,他在水流速度为4公里/小时的河中游泳.
(1)若他垂直游向河对岸,则他实际沿什么方向前进?实际前进的速度为多少?
(2)他必须朝哪个方向游,才能沿与水流垂直的方向前进?实际前进的速度为多少?
20. (本小题满分13分)
已知向量,,
(1)求函数的单调减区间;
(2)若函数的图象上各点纵坐标不变,横坐标缩短为原来的得到函数的图象,试求函数在的值域。
21(本小题满分14分)
在平面直角坐标系中,已知向量又点.
(1)若,且为坐标原点),求向量;
(2)若向量与向量共线,当,且取最大值4时,求.
济宁一中高一下学期数学试题参考答案
一.选择题:CDDCA BCDBA
二.填空题:11. , 12. 13. 14. 15. ②⑥
三.解答题:
16.解:(1.) 原式=
===1……………………………….6分
(2.)由得
则=
=== …………………………………………………………12分
17. 解:(1),
……………………………………………………4分
(2),
向量与垂直,
解得,
当时,向量与垂直……………………………………………8分
(3)向量与平行,
解得,此时
时,向量与共线同向…………………………………………12分
18. 解:由图可知,,,
将点代入得,
,又,
…………………………………………………………6分
(2)由得,
,
不等式的解集为……………………12分
19. 解:(1)如图①,设人游泳的速度为,水流的速度为,以、为邻边作OACB,则此人的实际速度为
图① 图②
在Rt△ACO中,由勾股定理知||=8 且∠COA=60°,
故此人沿与河岸成60°的夹角顺着水流的方向前进,速度大小为8公里/小时. ……………………………………………………………………………………………6分
(2)如图②,设此人的实际速度为,水流速度为,则游速为,在Rt△AOD中,.
故此人沿与河岸成的夹角逆着水流方向前进,实际前进的速度大小为4公里/小时. ……………………………………………………………12分
20. 解:(1)=,
令得
函数的单调减区间为.………………………………6分
(2)由题意知,
,,
,
函数在的值域为………………………………………………13分
21解:(1)可得,∵,∴,
得.则,又.
∴,解得,
当时,;当时,.
∴或.……………………………………………………………6分
(2)∵向量与向量共线,∴
∴,
.
∵,∴,故当时,取最大值,有,得.
这时,,,,得,则.
∴.……………………………………………………………14分
o
o
x
y
O
1
x
y
O
1
o
o
x
y
O
1
°
°
x
y
O
1
°
°
A
B
C
D
同课章节目录
