2023-2024学年人教版七年级数学上册1.2.4 绝对值 第1课时 课件(共17张PPT)
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册1.2.4 绝对值 第1课时 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 199.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 14:57:56 | ||
图片预览






文档简介
(共17张PPT)
第一章 有理数
1.2 有理数
1.2.4 绝对值 第1课时
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.知道绝对值的概念,会求一个有理数的绝对值;(重点)
2.通过具体的情境和数形两方面体会绝对值的意义和作用.
一、学习目标
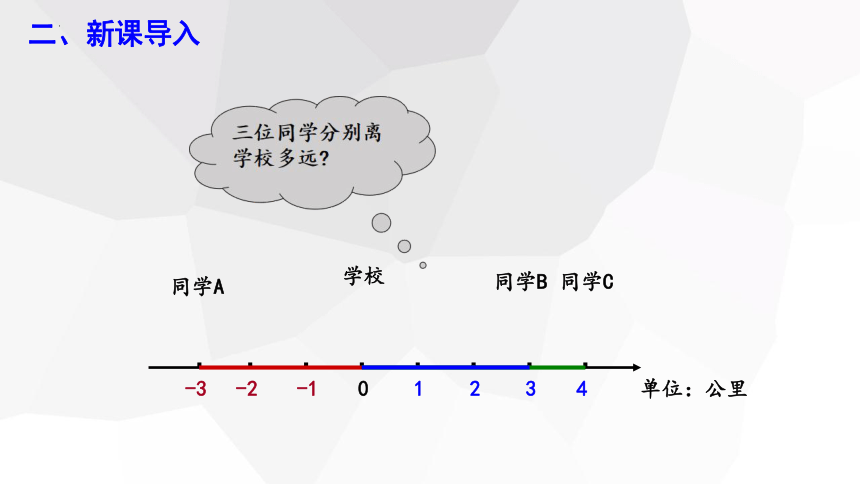
二、新课导入
0
1
2
3
4
-1
-2
-3
同学A
同学B
同学C
学校
单位:公里
三、概念剖析
一般地,数轴上表示数a的点与原点的距离叫做数a的绝
对值,记作|a|.
这里的数a可以是正数、负数和0
三、概念剖析
A, B两点分别表示数-10和10,它们与原点的距离都是
10个单位长度,所以-10和10的绝对值都是10,即 |-10|=
10,|10|=10.显然|0|=0.
思考:下图中A,B两点表示的数的绝对值是多少?0的绝对值是多少?
三、概念剖析
1.任何一个数的绝对值都是非负数(正数和0).
2.一个正数的绝对值是它本身;
3.一个负数的绝对值是它的相反数;
4.0的绝对值是0.
5.互为相反数的两个数,其绝对值相等.
性质:
四、典型例题
例1.填空
1.____的相反数是它本身,______的绝对值是它本身,______的
绝对值是它的相反数.
2.|-1|的相反数是 ;若| a |=2,则a= _____.
(一)理解绝对值的概念,求一个有理数的绝对值
0
非负数
非正数
1
±2
四、典型例题
例2.求以下各数的绝对值.12, , -7.5, 0.
(一)理解绝对值的概念,求一个有理数的绝对值
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
总结:求一个数的绝对值,只要利用绝对值符号来表示一个数的
绝对值,然后再利用绝对值的性质进行化简即可.即“一添二去”.
(添绝对值符号,再去掉绝对值符号)
四、典型例题
【当堂检测】
1.下列说法正确的是( )
A.一个数的绝对值等于本身,则这个数一定是正数
B.一个数的绝对值等于它的相反数,这个数一定是负数
C.如果两个数的绝对值相等,那么这两个数一定相等
D.有理数的绝对值一定是非负数
D
【当堂检测】
-b
a-b
0.2
2.化简
| 0.2 |=
| b |= (b<0)
| a – b | = (a>b)
| |=
四、典型例题
(二)绝对值的意义和作用
例3.甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程
数为正.两辆出租车都从0地出发,某一时刻甲、乙两车的位置分别为下图中A点和B点,则此时甲、乙两车离0地的距离是多少?A、B两点它们的实际意义是什么?
-5
5
0
O
B
A
解:|-5|=5,|5|=5,甲、乙两车离0地的距离都为5公里;
A点表示甲车向东行驶了5公里,B点表示乙车西东行驶了5公里.
总结:一个数的绝对值是表示该数的点与原点的距离,根据
题目中的条件确定绝对值符号内的数,再求其绝对值.
四、典型例题
【当堂检测】
3.求绝对值不大于2的整数.
由上图可知绝对值不大于2的整数有:0,±1, ±2.
解:画出数轴分析
【当堂检测】
4.数轴上点m 满足 ,则m的值为多少?
-1
1
0
O
2
3
●
解:这里 的几何意义为数轴上点m到点1的距离等于2,我们观察数轴发现到点1的距离为2的点有两个,分别是-1和3,所以m的值就是-1或3;
另外,我们也可以把m-1看做一个整体,把它想象成未知数x,这个式子就变成了 很容易的,我们得到x=2或-2,当x=2时,m就等于3,当x=-2时,m就等于-1.
五、课堂总结
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0
(2)
第一章 有理数
1.2 有理数
1.2.4 绝对值 第1课时
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.知道绝对值的概念,会求一个有理数的绝对值;(重点)
2.通过具体的情境和数形两方面体会绝对值的意义和作用.
一、学习目标
二、新课导入
0
1
2
3
4
-1
-2
-3
同学A
同学B
同学C
学校
单位:公里
三、概念剖析
一般地,数轴上表示数a的点与原点的距离叫做数a的绝
对值,记作|a|.
这里的数a可以是正数、负数和0
三、概念剖析
A, B两点分别表示数-10和10,它们与原点的距离都是
10个单位长度,所以-10和10的绝对值都是10,即 |-10|=
10,|10|=10.显然|0|=0.
思考:下图中A,B两点表示的数的绝对值是多少?0的绝对值是多少?
三、概念剖析
1.任何一个数的绝对值都是非负数(正数和0).
2.一个正数的绝对值是它本身;
3.一个负数的绝对值是它的相反数;
4.0的绝对值是0.
5.互为相反数的两个数,其绝对值相等.
性质:
四、典型例题
例1.填空
1.____的相反数是它本身,______的绝对值是它本身,______的
绝对值是它的相反数.
2.|-1|的相反数是 ;若| a |=2,则a= _____.
(一)理解绝对值的概念,求一个有理数的绝对值
0
非负数
非正数
1
±2
四、典型例题
例2.求以下各数的绝对值.12, , -7.5, 0.
(一)理解绝对值的概念,求一个有理数的绝对值
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
总结:求一个数的绝对值,只要利用绝对值符号来表示一个数的
绝对值,然后再利用绝对值的性质进行化简即可.即“一添二去”.
(添绝对值符号,再去掉绝对值符号)
四、典型例题
【当堂检测】
1.下列说法正确的是( )
A.一个数的绝对值等于本身,则这个数一定是正数
B.一个数的绝对值等于它的相反数,这个数一定是负数
C.如果两个数的绝对值相等,那么这两个数一定相等
D.有理数的绝对值一定是非负数
D
【当堂检测】
-b
a-b
0.2
2.化简
| 0.2 |=
| b |= (b<0)
| a – b | = (a>b)
| |=
四、典型例题
(二)绝对值的意义和作用
例3.甲、乙两辆出租车在一条东西走向的街道上行驶,记向东行驶的里程
数为正.两辆出租车都从0地出发,某一时刻甲、乙两车的位置分别为下图中A点和B点,则此时甲、乙两车离0地的距离是多少?A、B两点它们的实际意义是什么?
-5
5
0
O
B
A
解:|-5|=5,|5|=5,甲、乙两车离0地的距离都为5公里;
A点表示甲车向东行驶了5公里,B点表示乙车西东行驶了5公里.
总结:一个数的绝对值是表示该数的点与原点的距离,根据
题目中的条件确定绝对值符号内的数,再求其绝对值.
四、典型例题
【当堂检测】
3.求绝对值不大于2的整数.
由上图可知绝对值不大于2的整数有:0,±1, ±2.
解:画出数轴分析
【当堂检测】
4.数轴上点m 满足 ,则m的值为多少?
-1
1
0
O
2
3
●
解:这里 的几何意义为数轴上点m到点1的距离等于2,我们观察数轴发现到点1的距离为2的点有两个,分别是-1和3,所以m的值就是-1或3;
另外,我们也可以把m-1看做一个整体,把它想象成未知数x,这个式子就变成了 很容易的,我们得到x=2或-2,当x=2时,m就等于3,当x=-2时,m就等于-1.
五、课堂总结
1.数轴上表示数a的点与原点的距离叫做数a的绝对值.
2.绝对值的性质
(1)|a|≥0
(2)
