2023-2024学年人教版七年级数学上册1.4.2 有理数的除法 第1课时 课件(共16张PPT)
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册1.4.2 有理数的除法 第1课时 课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 564.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
第一章 有理数
1.4 有理数的乘除法
1.4.2 有理数的除法 第1课时
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.知道有理数的除法法则,能进行有理数的简单除法运算;
2.能运用倒数将乘法与除法相互转化,能将乘除混合运算统一为乘法运算;(重点)
3.理解分数与有理数除法的联系,能运用除法化简分数.
一、学习目标
二、新课导入
某班4名同学参加1000米跑步测试,以3分40秒为标准,超过一秒扣一分,低一秒加一分;记录如下+10,+2,-5,-17,则这4名同学平均分是多少?
列式:[(+10)+(+2)+(-5)+(-17)]÷4=
(-10)÷4
思考:如何计算(-10)÷4?
问题1:计算(-10)÷4
根据除法的意义,这就是说要求一个数,使它与4相乘等于-10;
因为(-2.5)×4=-10,所以(-10)÷4=-2.5
又因为(-10)× =-2.5,所以(-10)÷4 =(-10)×
三、概念剖析
问题2:计算:
(1)5÷(-2)= . 5×( )= .
(2)(-3)÷(-1)= . (-3)×(-1)= .
(3)3÷( )= . 3×( )= .
(4)4÷0=?
三、概念剖析
3
3
无意义,除数不能为0
思考:通过以上几例除法与乘法式子的比较,你能得到什么结论
-10
-10
三、概念剖析
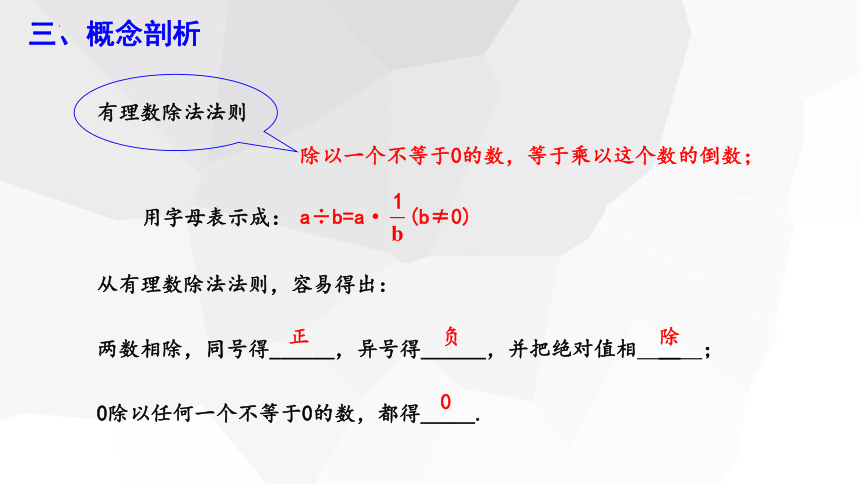
有理数除法法则
除以一个不等于0的数,等于乘以这个数的倒数;
从有理数除法法则,容易得出:
两数相除,同号得______,异号得______,并把绝对值相 __ ;
0除以任何一个不等于0的数,都得_____.
正
负
0
除
a÷b=a· (b≠0)
用字母表示成:
四、典型例题
(一)有理数的除法法则以及简单除法运算
例1.计算(1)(-27)÷9= ;
(2)4÷(-0.125)= .
-3
-32
总结:两个有理数的相除,先确定符号,再绝对值相除得出结果.
【当堂检测】
1.计算(1)(-3)÷0.25= ;
(2)( )÷ = ;
(3)0÷(-6)= .
-3
0
-12
【当堂检测】
2.有理数的除法法则,除以一个数等于乘以这个数的 ;
两数相除,同号得 , 异号得 .
倒数
正
负
四、典型例题
(二)将乘除混合运算统一为乘法运算
例2.计算 ×6÷( )
解:原式= ×6×(-5)
= 8×(-5)
= -40
总结:进行乘除混合运算,可以根据有理数除法法则将除法运算转化为乘法运算,再进行计算.
3.计算(-8)×(-2)÷( )的结果为( )
A. 16 B.-16 C.32 D.-32
【当堂检测】
D
【当堂检测】
解:原式 =
4.计算( ) ×( )÷( )÷3
( )×( )×( )×
= ( )× ×( )×( )
=
四、典型例题
(三)化简分数
例3.化简下列分数:(1) ; (2) .
解:(1) =(-15)÷3
= -5
(2) =(-27)÷(-12)
=
总结:分数可以理解为分子除以分母;
化简分数,能整除的可直接进行相除,不能整除的可约分处理.
【当堂检测】
5.化简分数: = ; = .
-6
五、课堂总结
2.两数相除,同号得正,异号得负,并把绝对值相除;
3.0除以任何一个不等于0的数,都得0;0不能作为除数;
4.分数可以理解为分子除以分母;
化简分数,能整除的可直接进行相除,不能整除的可约分处理.
1.有理数除法法则:除以一个不等于0的数,等于乘以这个数的倒数;
a÷b = a· (b≠0);
用字母表示成:
第一章 有理数
1.4 有理数的乘除法
1.4.2 有理数的除法 第1课时
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.知道有理数的除法法则,能进行有理数的简单除法运算;
2.能运用倒数将乘法与除法相互转化,能将乘除混合运算统一为乘法运算;(重点)
3.理解分数与有理数除法的联系,能运用除法化简分数.
一、学习目标
二、新课导入
某班4名同学参加1000米跑步测试,以3分40秒为标准,超过一秒扣一分,低一秒加一分;记录如下+10,+2,-5,-17,则这4名同学平均分是多少?
列式:[(+10)+(+2)+(-5)+(-17)]÷4=
(-10)÷4
思考:如何计算(-10)÷4?
问题1:计算(-10)÷4
根据除法的意义,这就是说要求一个数,使它与4相乘等于-10;
因为(-2.5)×4=-10,所以(-10)÷4=-2.5
又因为(-10)× =-2.5,所以(-10)÷4 =(-10)×
三、概念剖析
问题2:计算:
(1)5÷(-2)= . 5×( )= .
(2)(-3)÷(-1)= . (-3)×(-1)= .
(3)3÷( )= . 3×( )= .
(4)4÷0=?
三、概念剖析
3
3
无意义,除数不能为0
思考:通过以上几例除法与乘法式子的比较,你能得到什么结论
-10
-10
三、概念剖析
有理数除法法则
除以一个不等于0的数,等于乘以这个数的倒数;
从有理数除法法则,容易得出:
两数相除,同号得______,异号得______,并把绝对值相 __ ;
0除以任何一个不等于0的数,都得_____.
正
负
0
除
a÷b=a· (b≠0)
用字母表示成:
四、典型例题
(一)有理数的除法法则以及简单除法运算
例1.计算(1)(-27)÷9= ;
(2)4÷(-0.125)= .
-3
-32
总结:两个有理数的相除,先确定符号,再绝对值相除得出结果.
【当堂检测】
1.计算(1)(-3)÷0.25= ;
(2)( )÷ = ;
(3)0÷(-6)= .
-3
0
-12
【当堂检测】
2.有理数的除法法则,除以一个数等于乘以这个数的 ;
两数相除,同号得 , 异号得 .
倒数
正
负
四、典型例题
(二)将乘除混合运算统一为乘法运算
例2.计算 ×6÷( )
解:原式= ×6×(-5)
= 8×(-5)
= -40
总结:进行乘除混合运算,可以根据有理数除法法则将除法运算转化为乘法运算,再进行计算.
3.计算(-8)×(-2)÷( )的结果为( )
A. 16 B.-16 C.32 D.-32
【当堂检测】
D
【当堂检测】
解:原式 =
4.计算( ) ×( )÷( )÷3
( )×( )×( )×
= ( )× ×( )×( )
=
四、典型例题
(三)化简分数
例3.化简下列分数:(1) ; (2) .
解:(1) =(-15)÷3
= -5
(2) =(-27)÷(-12)
=
总结:分数可以理解为分子除以分母;
化简分数,能整除的可直接进行相除,不能整除的可约分处理.
【当堂检测】
5.化简分数: = ; = .
-6
五、课堂总结
2.两数相除,同号得正,异号得负,并把绝对值相除;
3.0除以任何一个不等于0的数,都得0;0不能作为除数;
4.分数可以理解为分子除以分母;
化简分数,能整除的可直接进行相除,不能整除的可约分处理.
1.有理数除法法则:除以一个不等于0的数,等于乘以这个数的倒数;
a÷b = a· (b≠0);
用字母表示成:
