2023-2024学年人教版七年级数学上册1.5.1 乘方 第1课时 课件(共14张PPT)
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册1.5.1 乘方 第1课时 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 379.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览





文档简介
(共14张PPT)
第一章 有理数
1.5 有理数的乘方
1.5.1 乘方 第1课时
1.理解并掌握有理数的乘方、幂、底数、指数的概念及意义;
2.能够正确进行有理数的乘方运算;(重点)
3.经历从乘法到乘方的推导过程,从中感受转化的数学思想.
一、学习目标
二、新课导入
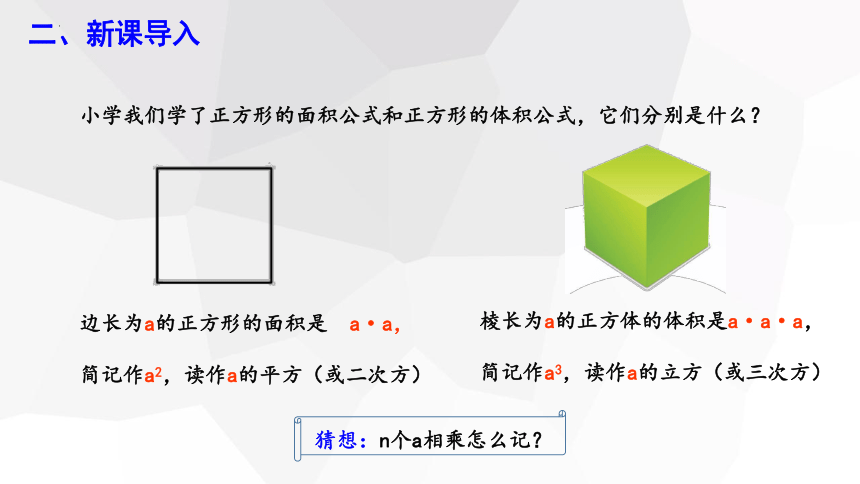
小学我们学了正方形的面积公式和正方形的体积公式,它们分别是什么?
猜想:n个a相乘怎么记?
边长为a的正方形的面积是 a·a,
简记作a2,读作a的平方(或二次方)
棱长为a的正方体的体积是a·a·a,
简记作a3,读作a的立方(或三次方)
三、概念剖析
求n个相同因数的积的运算,叫做乘方;乘方的结果叫做幂.
一般地,n个相同的因数a相乘,即a·a·a·…·a 记做an,读做a的n次方.
n个a
三、概念剖析
an
底数
幂
指数
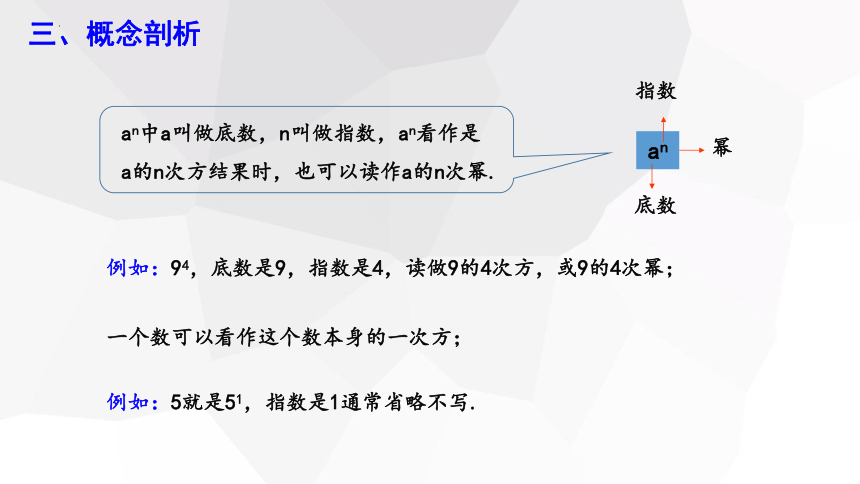
an中a叫做底数,n叫做指数,an看作是
a的n次方结果时,也可以读作a的n次幂.
例如:94,底数是9,指数是4,读做9的4次方,或9的4次幂;
一个数可以看作这个数本身的一次方;
例如:5就是51,指数是1通常省略不写.
例1.计算:(1)(-2)3; (2)(-2)4 ; (3)33 .
解:(1)(-2)3 = (-2)×(-2)×(-2)= 4×(-2) = -8;
(2)(-2)4 = (-2)×(-2)×(-2)×(-2) = 16;
(3) 33 = 3×3×3 = 27.
你发现了什么规律?
四、典型例题
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
显然,正数的任何次幂都是正数,0的任何次幂都是0.
四、典型例题
1.计算:(1)(-3)4 ; (2)(-6)3 .
解:(1)(-3)4 = (-3)×(-3)×(-3)×(-3) = 81;
(2)(-6)3 = (-6)×(-6)×(-6) = -216.
【当堂检测】
四、典型例题
例2.计算(1)(-0.2)4 ; (2)∣-4∣3 .
解:(1)(-0.2)4 = (-0.2)×(-0.2)×(-0.2)×(-0.2) = 0.0016;
(2)|-4|3 = 43 = 4×4×4 = 64.
【当堂检测】
2.计算:(1)(-0.1)3 ; (2)( )4 .
解:(1)(-0.1)3
=(-0.1)×(-0.1)×(-0.1)
= 0.01×(-0.1)
= -0.001
(2)原式
3.一个数的平方等于36那么这个数是 ;0的5次方是 .
±6
0
【当堂检测】
四、典型例题
例3.有一根铁丝长100cm,第一次截去一半,第二次截去剩下部分的一半,如此截下去,第五次后剩下的铁丝有多长?
分析:第一次截完后剩下之前长度的 ,
后面每次截完后剩下上一次长度的 ;
解:根据题意得100×( )5 =100× = (cm);
答:第五次后剩下的铁丝有 cm .
【当堂检测】
4.看过电视剧《西游记》的同学,一定很喜欢孙悟空,孙悟空的金箍棒能随意伸缩,假设它最短时只有1厘米,第1次变化后变成3厘米,第2次变化后变成9厘米,第3次变化后变成27厘米……照此规律变化下去,到第5次变化后金箍棒的长是 厘米;第n次变化是 厘米.
243
3n
五、课堂总结
1.乘方的概念:
n个相同的因数a相乘,即a·a·a·…·a 记做an,
读做a的n次方.
n个a
an
底数
幂
指数
2.乘方符号的确定:
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
显然,正数的任何次幂都是整数,0的任何次幂都是0.
第一章 有理数
1.5 有理数的乘方
1.5.1 乘方 第1课时
1.理解并掌握有理数的乘方、幂、底数、指数的概念及意义;
2.能够正确进行有理数的乘方运算;(重点)
3.经历从乘法到乘方的推导过程,从中感受转化的数学思想.
一、学习目标
二、新课导入
小学我们学了正方形的面积公式和正方形的体积公式,它们分别是什么?
猜想:n个a相乘怎么记?
边长为a的正方形的面积是 a·a,
简记作a2,读作a的平方(或二次方)
棱长为a的正方体的体积是a·a·a,
简记作a3,读作a的立方(或三次方)
三、概念剖析
求n个相同因数的积的运算,叫做乘方;乘方的结果叫做幂.
一般地,n个相同的因数a相乘,即a·a·a·…·a 记做an,读做a的n次方.
n个a
三、概念剖析
an
底数
幂
指数
an中a叫做底数,n叫做指数,an看作是
a的n次方结果时,也可以读作a的n次幂.
例如:94,底数是9,指数是4,读做9的4次方,或9的4次幂;
一个数可以看作这个数本身的一次方;
例如:5就是51,指数是1通常省略不写.
例1.计算:(1)(-2)3; (2)(-2)4 ; (3)33 .
解:(1)(-2)3 = (-2)×(-2)×(-2)= 4×(-2) = -8;
(2)(-2)4 = (-2)×(-2)×(-2)×(-2) = 16;
(3) 33 = 3×3×3 = 27.
你发现了什么规律?
四、典型例题
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
显然,正数的任何次幂都是正数,0的任何次幂都是0.
四、典型例题
1.计算:(1)(-3)4 ; (2)(-6)3 .
解:(1)(-3)4 = (-3)×(-3)×(-3)×(-3) = 81;
(2)(-6)3 = (-6)×(-6)×(-6) = -216.
【当堂检测】
四、典型例题
例2.计算(1)(-0.2)4 ; (2)∣-4∣3 .
解:(1)(-0.2)4 = (-0.2)×(-0.2)×(-0.2)×(-0.2) = 0.0016;
(2)|-4|3 = 43 = 4×4×4 = 64.
【当堂检测】
2.计算:(1)(-0.1)3 ; (2)( )4 .
解:(1)(-0.1)3
=(-0.1)×(-0.1)×(-0.1)
= 0.01×(-0.1)
= -0.001
(2)原式
3.一个数的平方等于36那么这个数是 ;0的5次方是 .
±6
0
【当堂检测】
四、典型例题
例3.有一根铁丝长100cm,第一次截去一半,第二次截去剩下部分的一半,如此截下去,第五次后剩下的铁丝有多长?
分析:第一次截完后剩下之前长度的 ,
后面每次截完后剩下上一次长度的 ;
解:根据题意得100×( )5 =100× = (cm);
答:第五次后剩下的铁丝有 cm .
【当堂检测】
4.看过电视剧《西游记》的同学,一定很喜欢孙悟空,孙悟空的金箍棒能随意伸缩,假设它最短时只有1厘米,第1次变化后变成3厘米,第2次变化后变成9厘米,第3次变化后变成27厘米……照此规律变化下去,到第5次变化后金箍棒的长是 厘米;第n次变化是 厘米.
243
3n
五、课堂总结
1.乘方的概念:
n个相同的因数a相乘,即a·a·a·…·a 记做an,
读做a的n次方.
n个a
an
底数
幂
指数
2.乘方符号的确定:
根据有理数的乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数.
显然,正数的任何次幂都是整数,0的任何次幂都是0.
