3.1.2 等式的性质 课件(共35张PPT)2023-2024学年人教版七年级数学上册
文档属性
| 名称 | 3.1.2 等式的性质 课件(共35张PPT)2023-2024学年人教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 360.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 15:28:14 | ||
图片预览






文档简介
(共35张PPT)
第三章 一元一次方程
3.1 从算式到方程
3.1.2 等式的性质
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1、理解等式的两条基本性质。
2、会用等式的基本性质解简单的一元一次程,并检验方程。
一、学习目标
二、新课导入
3+2=5; 3x+5=4; a+b=b+a;
6=2×3; S=ab; x-2=7.
观察上面式子表示了什么关系?
相等关系
像这样用等号“=”来表示相等关系的式子叫作等式.
右
左
观察:
三、概念剖析
b
三、概念剖析
右
左
b
a
三、概念剖析
右
左
a
b
三、概念剖析
右
左
a
b
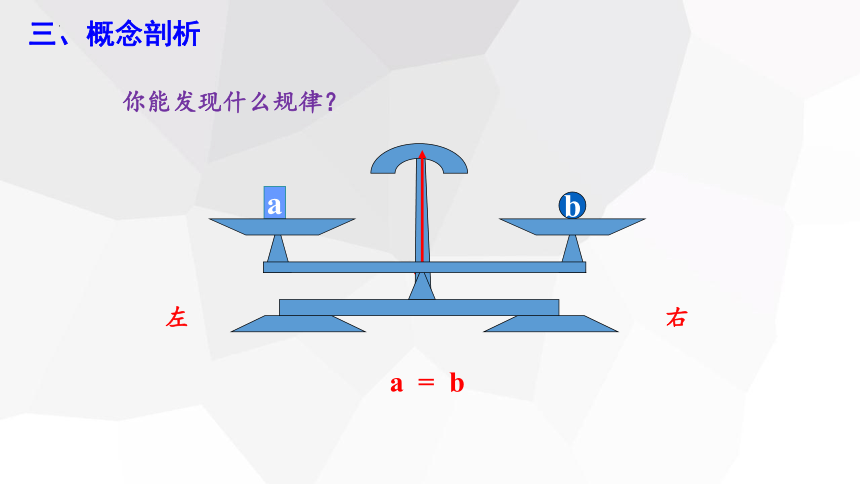
你能发现什么规律?
三、概念剖析
右
左
a = b
a
b
c
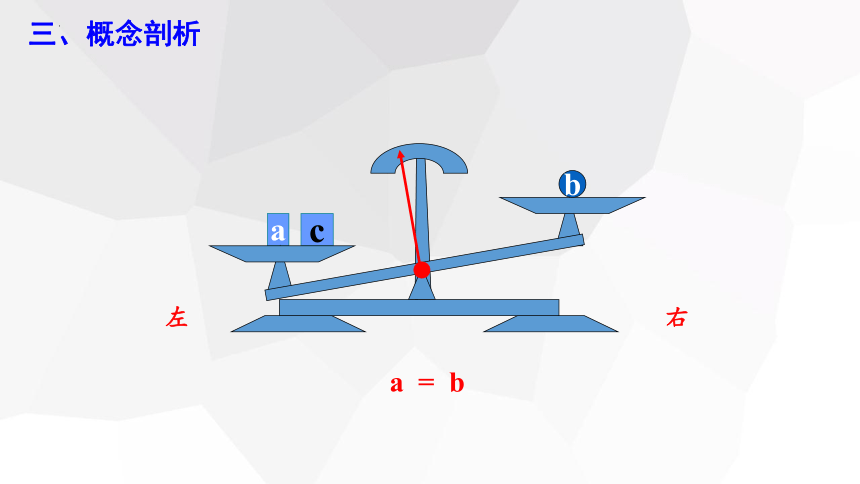
a = b
右
左
三、概念剖析
c
a
b
右
左
a = b
三、概念剖析
b
c
a
右
左
a = b
三、概念剖析
c
a
c
b
右
左
a = b
三、概念剖析
c
a
c
b
a+c b+c
=
你能发现什么规律?
右
左
a = b
三、概念剖析
c
c
b
a
右
左
a = b
三、概念剖析
c
b
a
右
左
a = b
三、概念剖析
c
b
a
右
左
a = b
三、概念剖析
a
b
右
左
a = b
三、概念剖析
你能发现什么规律?
a-c = b-c
a
b
右
左
a = b
三、概念剖析
等式的性质1:
等式的两边加(或减)同一个数(或式子),结果仍相等。
三、概念剖析
a
b
a = b
右
左
三、概念剖析
a
b
b
a
2a = 2b
右
左
三、概念剖析
a = b
a
b
a
a
b
b
右
左
三、概念剖析
a = b
3a = 3b
a
b
a
a
a
a
a
a
b
b
b
b
b
b
C个
C个
右
左
三、概念剖析
a = b
ac = bc
三、概念剖析
a = b
a
b
右
左
等式的性质2:
等式的两边乘同一个数,或除以同一个不为0的数,结果仍相等。
三、概念剖析
回答:
三、概念剖析
1.从x=y能否得到x+5=y+5 为什么
答:可以;根据等式的性质1,等式的两边加(或减)同一个数(或式子),结果仍相等.
2.从x=y能否得到 = 为什么?
答:可以;根据等式的性质2,等式的两边乘同一个数,或除以同一个不为0的数,结果仍相等.
答:不一定;如果c不为0,则根据等式的性质2可以.如果c为0则不能.
3.由a=b能不能得到 呢?为什么?
三、概念剖析
四、典型例题
例题1:用等式的性质解方程
(1)x+7=26
解:两边都减7,得x+7-7=26-7
x=19
注:“解方程”就是利用等式的性质求方程中未知数的值,把原方程化成x=a的形式(即x的系数是1为止).
四、典型例题
(2) -5x=20
解:(2)两边同除以-5,得:
所以 x=-4
(3)
两边同乘以-3得:x=-27
解:(3)两边同加5,得:
注意:
①两边必须同时进行计算;
②加(或减)的数必须是同一个数.
的解是x=-27。对吗
检验:把 x=-27代入原方程的两边
左边=4
右边=4
左边=右边
所以x=-27是原方程的解。
四、典型例题
检验方程的解
2.如果4x=-12y,4x÷4= ,
3.如果-0.2x=6,-0.2x÷(-0.2)= ,
1.如果x-3=2,x-3+3= ,
(根据等式性质1,在等式两边同加3)
2+3
-12y÷4
(根据等式性质2,在等式两边同时除以4)
(根据等式性质2,在等式两边同除-0.2)
6÷(-0.2)
【当堂检测】
【当堂检测】
4.解下列方程并检验
(1)x+8=13
解:方程两边同时减去8,
即:x+8-8=13-8
得 x=5
检验:将x=5代入方程得,
左边=5+8=13=右边
故x=5是原方程的解
(2)0.5x=6
解:方程两边同时乘以2,
即:2×0.5x=6
得 x=6
检验:将x=6代入方程得,
左边=2×0.5×6=6=右边
故x=6是原方程的解
【当堂检测】
4.解下列方程并检验
(3)3x+8=11
解:方程两边同时减去8,
即:3x+8-8=11-8
得 3x=3
两边同时除以3得:x=1
检验:将x=1代入方程得,
左边=3+8=11=右边
故x=1是原方程的解
(4)4-0.5x=6
解:方程两边同时减去4,
即:4-0.5x-4=6-4
得 -0.5x=2
两边同时乘以-2得:x=-4
检验:将x=-4代入方程得,
左边=4-0.5×(-4)=6=右边
故x=-4是原方程的解
等式性质1: 等式两边加(或减)同一个数(或式子),结果仍相等。
如果a=b 那么a+c=b+c
等式性质2: 等式两边乘同一个数或 除以同一个不为0的数,结果
仍相等。
如果a=b 那么ac=bc
如果a=b 那么
掌握关键: (1)“两边”“同一个数(或式子)”
(2)“除以同一个不为0的数”
五、课堂总结
第三章 一元一次方程
3.1 从算式到方程
3.1.2 等式的性质
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1、理解等式的两条基本性质。
2、会用等式的基本性质解简单的一元一次程,并检验方程。
一、学习目标
二、新课导入
3+2=5; 3x+5=4; a+b=b+a;
6=2×3; S=ab; x-2=7.
观察上面式子表示了什么关系?
相等关系
像这样用等号“=”来表示相等关系的式子叫作等式.
右
左
观察:
三、概念剖析
b
三、概念剖析
右
左
b
a
三、概念剖析
右
左
a
b
三、概念剖析
右
左
a
b
你能发现什么规律?
三、概念剖析
右
左
a = b
a
b
c
a = b
右
左
三、概念剖析
c
a
b
右
左
a = b
三、概念剖析
b
c
a
右
左
a = b
三、概念剖析
c
a
c
b
右
左
a = b
三、概念剖析
c
a
c
b
a+c b+c
=
你能发现什么规律?
右
左
a = b
三、概念剖析
c
c
b
a
右
左
a = b
三、概念剖析
c
b
a
右
左
a = b
三、概念剖析
c
b
a
右
左
a = b
三、概念剖析
a
b
右
左
a = b
三、概念剖析
你能发现什么规律?
a-c = b-c
a
b
右
左
a = b
三、概念剖析
等式的性质1:
等式的两边加(或减)同一个数(或式子),结果仍相等。
三、概念剖析
a
b
a = b
右
左
三、概念剖析
a
b
b
a
2a = 2b
右
左
三、概念剖析
a = b
a
b
a
a
b
b
右
左
三、概念剖析
a = b
3a = 3b
a
b
a
a
a
a
a
a
b
b
b
b
b
b
C个
C个
右
左
三、概念剖析
a = b
ac = bc
三、概念剖析
a = b
a
b
右
左
等式的性质2:
等式的两边乘同一个数,或除以同一个不为0的数,结果仍相等。
三、概念剖析
回答:
三、概念剖析
1.从x=y能否得到x+5=y+5 为什么
答:可以;根据等式的性质1,等式的两边加(或减)同一个数(或式子),结果仍相等.
2.从x=y能否得到 = 为什么?
答:可以;根据等式的性质2,等式的两边乘同一个数,或除以同一个不为0的数,结果仍相等.
答:不一定;如果c不为0,则根据等式的性质2可以.如果c为0则不能.
3.由a=b能不能得到 呢?为什么?
三、概念剖析
四、典型例题
例题1:用等式的性质解方程
(1)x+7=26
解:两边都减7,得x+7-7=26-7
x=19
注:“解方程”就是利用等式的性质求方程中未知数的值,把原方程化成x=a的形式(即x的系数是1为止).
四、典型例题
(2) -5x=20
解:(2)两边同除以-5,得:
所以 x=-4
(3)
两边同乘以-3得:x=-27
解:(3)两边同加5,得:
注意:
①两边必须同时进行计算;
②加(或减)的数必须是同一个数.
的解是x=-27。对吗
检验:把 x=-27代入原方程的两边
左边=4
右边=4
左边=右边
所以x=-27是原方程的解。
四、典型例题
检验方程的解
2.如果4x=-12y,4x÷4= ,
3.如果-0.2x=6,-0.2x÷(-0.2)= ,
1.如果x-3=2,x-3+3= ,
(根据等式性质1,在等式两边同加3)
2+3
-12y÷4
(根据等式性质2,在等式两边同时除以4)
(根据等式性质2,在等式两边同除-0.2)
6÷(-0.2)
【当堂检测】
【当堂检测】
4.解下列方程并检验
(1)x+8=13
解:方程两边同时减去8,
即:x+8-8=13-8
得 x=5
检验:将x=5代入方程得,
左边=5+8=13=右边
故x=5是原方程的解
(2)0.5x=6
解:方程两边同时乘以2,
即:2×0.5x=6
得 x=6
检验:将x=6代入方程得,
左边=2×0.5×6=6=右边
故x=6是原方程的解
【当堂检测】
4.解下列方程并检验
(3)3x+8=11
解:方程两边同时减去8,
即:3x+8-8=11-8
得 3x=3
两边同时除以3得:x=1
检验:将x=1代入方程得,
左边=3+8=11=右边
故x=1是原方程的解
(4)4-0.5x=6
解:方程两边同时减去4,
即:4-0.5x-4=6-4
得 -0.5x=2
两边同时乘以-2得:x=-4
检验:将x=-4代入方程得,
左边=4-0.5×(-4)=6=右边
故x=-4是原方程的解
等式性质1: 等式两边加(或减)同一个数(或式子),结果仍相等。
如果a=b 那么a+c=b+c
等式性质2: 等式两边乘同一个数或 除以同一个不为0的数,结果
仍相等。
如果a=b 那么ac=bc
如果a=b 那么
掌握关键: (1)“两边”“同一个数(或式子)”
(2)“除以同一个不为0的数”
五、课堂总结
