2023-2024学年人教版七年级数学上册1.5.2 科学计数法 课件(共15张PPT)
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册1.5.2 科学计数法 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第一章 有理数
1.5 有理数的乘方
1.5.2 科学记数法
1.理解科学记数法的意义,学会用科学记数法表示比10大的数;
2.经历用科学记数法表示大数的过程,体验科学记数法表示大数
的优越性.
一、学习目标
二、新课导入
2019年,世界人口达到 7600 000 000
太阳半径约696 000 000米
生活中的大数
二、新课导入
光速飞船速度约300 000 000米/秒
中国高铁线路总长度突破20 000 000米
思考:在上面的例子中,我们遇到了很多非常大的数,读和记都很不方便,
有没有一种简单的方法来处理这种情况呢?
那么100 000可以写成 ,10 000 000可以写成 ;
102 = ,103 = ,104 = ;
三、概念剖析
填一填:
1后面有11个零呢?
100
1000
10000
105
1011
107
(一)10n 的特征
一般地,10的n次幂,在1的后面有几个0 就等于10的几次方.
三、概念剖析
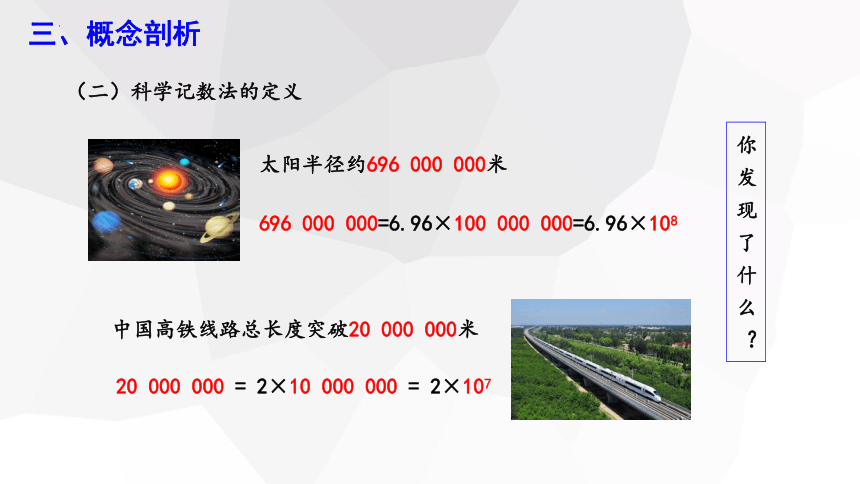
(二)科学记数法的定义
太阳半径约696 000 000米
696 000 000=6.96×100 000 000=6.96×108
中国高铁线路总长度突破20 000 000米
20 000 000 = 2×10 000 000 = 2×107
你 发 现 了 什 么 ?
三、概念剖析
把一个大于10的数记a×10n的形式,其中a是整数位数只有一位的数这种记数方法叫做科学记数法.
注意:科学记数法的形式为a×10n ,其中1≤a<10,n 为正整数.
四、典型例题
(一)用科学记数法表示数
例1.用科学记数法表示下列各数:
(1)150 000 000;
(2)-123 000 000.
解:(1)150 000 000=1.5×108;
(2)-123 000 000=-1.23×108.
四、典型例题
例2.将下列用科学计数法表示的数字还原成原数
(1)1.35×106;
(2)-2.61×107.
解:(1)1.35×106 = 1 350 000;
(2)-2.61×107 = -26 100 000.
【当堂检测】
1.用科学记数法表示下列各数:
① 800 000 = ; ② -30 000 = ;
③ 65.54 = ; ④ -21 050 000 = .
6.554×10
8×105
-3×104
-2.105×107
【当堂检测】
2.已知下列用科学记数法表示的数,写出原来的数:
① 3.14×103 =____________; ② -6.28×107 = ;
③ -5.12×106 =___________; ④ 2.004×102 =____________.
3 140
-62 800 000
-5 120 000
200.4
四、典型例题
例3.据测算,我国每天因土地沙漠化造成的经济损失约为150 000 000元,若一年按365天计算,用科学记数法表示我国一年因土地沙漠化造成的经济损失.
(二)科学记数法的实际应用
解:150 000 000×365 = 54 750 000 000 = 5.475×1010元;
答:我国一年因土地沙漠化造成的经济损失为5.475×1010元.
四、典型例题
例4.科学家研究发现,每公顷的森林可吸收二氧化碳约1.5吨,我国人工林累计面积达
48 000 000公顷,这48 000 000公顷人工林可吸收多少吨二氧化碳.(用科学记数法表示)
解:48 000 000×1.5 = 72 000 000 = 7.2×107 吨;
答:48 000 000 公顷人工林可吸收 7.2×107 吨二氧化碳.
【当堂检测】
3.共享单车为市民短距离出行带来了极大便利.据2018年“深圳互联网自行车发展评估报告”披露,深圳市日均使用共享单车2590000人次,其中
2 590 000用科学记数法表示为( )
A.259×104 B.25.9×105
C.2.59×106 D.0.259×107
C
五、课堂总结
1.遇到较大的数时可用科学记数法来表示.
2.用科学记数法a×10n表示大数关键要注意两点:
(1)1≤a<10;
(2)当大数是大于10的整数时,n为整数位数减去1.
一般形式: a×10n( 1≤a<10,n为正整数)
第一章 有理数
1.5 有理数的乘方
1.5.2 科学记数法
1.理解科学记数法的意义,学会用科学记数法表示比10大的数;
2.经历用科学记数法表示大数的过程,体验科学记数法表示大数
的优越性.
一、学习目标
二、新课导入
2019年,世界人口达到 7600 000 000
太阳半径约696 000 000米
生活中的大数
二、新课导入
光速飞船速度约300 000 000米/秒
中国高铁线路总长度突破20 000 000米
思考:在上面的例子中,我们遇到了很多非常大的数,读和记都很不方便,
有没有一种简单的方法来处理这种情况呢?
那么100 000可以写成 ,10 000 000可以写成 ;
102 = ,103 = ,104 = ;
三、概念剖析
填一填:
1后面有11个零呢?
100
1000
10000
105
1011
107
(一)10n 的特征
一般地,10的n次幂,在1的后面有几个0 就等于10的几次方.
三、概念剖析
(二)科学记数法的定义
太阳半径约696 000 000米
696 000 000=6.96×100 000 000=6.96×108
中国高铁线路总长度突破20 000 000米
20 000 000 = 2×10 000 000 = 2×107
你 发 现 了 什 么 ?
三、概念剖析
把一个大于10的数记a×10n的形式,其中a是整数位数只有一位的数这种记数方法叫做科学记数法.
注意:科学记数法的形式为a×10n ,其中1≤a<10,n 为正整数.
四、典型例题
(一)用科学记数法表示数
例1.用科学记数法表示下列各数:
(1)150 000 000;
(2)-123 000 000.
解:(1)150 000 000=1.5×108;
(2)-123 000 000=-1.23×108.
四、典型例题
例2.将下列用科学计数法表示的数字还原成原数
(1)1.35×106;
(2)-2.61×107.
解:(1)1.35×106 = 1 350 000;
(2)-2.61×107 = -26 100 000.
【当堂检测】
1.用科学记数法表示下列各数:
① 800 000 = ; ② -30 000 = ;
③ 65.54 = ; ④ -21 050 000 = .
6.554×10
8×105
-3×104
-2.105×107
【当堂检测】
2.已知下列用科学记数法表示的数,写出原来的数:
① 3.14×103 =____________; ② -6.28×107 = ;
③ -5.12×106 =___________; ④ 2.004×102 =____________.
3 140
-62 800 000
-5 120 000
200.4
四、典型例题
例3.据测算,我国每天因土地沙漠化造成的经济损失约为150 000 000元,若一年按365天计算,用科学记数法表示我国一年因土地沙漠化造成的经济损失.
(二)科学记数法的实际应用
解:150 000 000×365 = 54 750 000 000 = 5.475×1010元;
答:我国一年因土地沙漠化造成的经济损失为5.475×1010元.
四、典型例题
例4.科学家研究发现,每公顷的森林可吸收二氧化碳约1.5吨,我国人工林累计面积达
48 000 000公顷,这48 000 000公顷人工林可吸收多少吨二氧化碳.(用科学记数法表示)
解:48 000 000×1.5 = 72 000 000 = 7.2×107 吨;
答:48 000 000 公顷人工林可吸收 7.2×107 吨二氧化碳.
【当堂检测】
3.共享单车为市民短距离出行带来了极大便利.据2018年“深圳互联网自行车发展评估报告”披露,深圳市日均使用共享单车2590000人次,其中
2 590 000用科学记数法表示为( )
A.259×104 B.25.9×105
C.2.59×106 D.0.259×107
C
五、课堂总结
1.遇到较大的数时可用科学记数法来表示.
2.用科学记数法a×10n表示大数关键要注意两点:
(1)1≤a<10;
(2)当大数是大于10的整数时,n为整数位数减去1.
一般形式: a×10n( 1≤a<10,n为正整数)
