2023-2024学年人教版七年级数学上册3.3 去括号去分母 第1课时 课件(共15张PPT)
文档属性
| 名称 | 2023-2024学年人教版七年级数学上册3.3 去括号去分母 第1课时 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 407.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第三章 一元一次方程
3.3 解一元一次方程(二)
3.3.1 去括号
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.掌握去括号解一元一次方程的方法
2.会应用去括号、移项、合并同类项、系数化为1的方法解一元一次方程
3.通过解方程明确数学的化归思想
一、学习目标
二、新课导入
生活中,我们在吃鸡蛋等带壳的食物的时候,要先去壳;而在我们的数学中,解形如6x-3(x+2)=3这样带“壳”的方程的时候也要先去掉这层壳,方便我们“大快朵颐”,怎么来去“壳”呢?
例1:某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
提示:月平均用电量×n(月数)=n个月用电量
所有分量之和=总量
三、典型例题
下面我们通过实际的例子来详细学习“去壳”的过程
分析:若设上半年每月平均用电x度,
则下半年每月平均用电 度
上半年共用电 度,
下半年共用电 度.
因为全年共用了15万度电,
所以,可列方程_________________________.
(x-2000)
6(x-2000)
6x
6x+ 6(x-2000)=150000
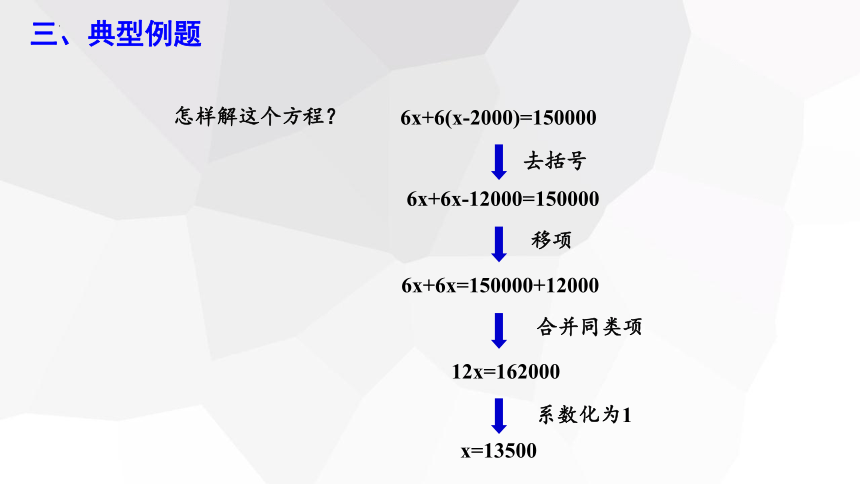
三、典型例题
6x+6(x-2000)=150000
6x+6x-12000=150000
x=13500
去括号
合并同类项
移项
6x+6x=150000+12000
系数化为1
12x=162000
怎样解这个方程?
三、典型例题
去括号解一元一次方程的一般步骤及注意事项
步骤 注意事项
去括号 注意符号,防止漏乘;
移项 移项要变号,防止漏项;
合并同类项 系数为1或-1时,记得省略1;
系数化为1 方程两边都除以系数,分子、分母不要写倒了;
三、典型例题
例2:解方程
去括号,得2x-x-10=5x+2x-2
移项,得2x-x-5x-2x=-2+10
合并同类项,得-6x=8
系数化为1,得x=-4/3
解:
三、典型例题
3x-7(x-1)= 3-2(x+3).
解:去括号,得3x-7x+7=3-2x-6
移项,得3x-7x+2x=3-6-7
合并同类项,得-2x=-10
系数化为1,得x=5
2x-(x+10)=5x+2(x-1)
(1)6x=-2(3x-5)+10; (2)-2(x+5)=3(x-5)-6
1.解下列方程
解:
(1)6x=-2(3x-5)+10
6x=-6x+10+10
6x+6x=10+10
12x=20
(2)-2(x+5)=3(x-5)-6
-2x-10=3x-15-6
-2x-3x=-15-6+10
-5x=-11
【当堂检测】
三、典型例题
例3:一艘船从甲码头到乙码头顺流而行,用了2 h;从乙码头返回甲码头逆流而行,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的平均速度.
分析:我们知道这艘船往返路程不变.
顺流速度=船在静水中速度+水流速度
顺流时间=2 h
逆流速度=船在静水中速度-水流速度
逆流时间=2.5 h
等量关系:往返路程不变
解:设船在静水中的平均速度为x km/h,则顺流速度为(x+3)km/h,逆流速度为(x-3)km/h.
根据往返路程相等,可列方程:
2(x+3)=2.5(x-3).
去括号,得: 2x+6=2.5x-7.5.
移项及合并同类项,得: -0.5x=-13.5.
系数化,1,得: x=27.
答:船在静水中的平均速度为27 km/h.
三、典型例题
2. 某轮船从A码头到B码头顺水航行3小时,返航时用4.5小时,已知轮船在静水中的速度为4千米/小时,求水流速度为多少?
解:顺流航行的路程=逆流航行的路程;设水流速度为x千米/时,则顺流速度为 千米/时,逆流速度为 千米/时,
(x+4)
(4-x)
由题意得: 3(x+4)=4.5(4-x)
解之得: x=0.8.
答:水流速度为0.8千米/时.
【当堂检测】
3. 七年级170名学生参加植树活动,如果每个男生平均一天能挖树坑3个,每个女生平均一天能种树7棵,正好能使每个树坑种上一棵树,则该年级的男生,女生各有多少人?
解:设该年级男生有x人,则女生有(170-x)人.由题意得:
3x=7(170-x)
系数化为1: x=119
则女生为170-119=51(人)
答:男生有119人,女生有51人.
去括号: 3x=1190-7x
移项及合并: 10x=1190
【当堂检测】
本节课学习了什么?
1.解一元一次方程的步骤:
去括号 移项 合并同类项 系数化为1
(1)去括号法则:①去括号,看符号;②是“十”,不变号;③是“-”,全变号.
(2)括号前有因数时,不要漏乘如:2(x-3)= 2x-6
四、课堂总结
2.需要注意的是:
第三章 一元一次方程
3.3 解一元一次方程(二)
3.3.1 去括号
学习导航
学习目标
新课导入
概念剖析
典型例题
当堂检测
课堂总结
1.掌握去括号解一元一次方程的方法
2.会应用去括号、移项、合并同类项、系数化为1的方法解一元一次方程
3.通过解方程明确数学的化归思想
一、学习目标
二、新课导入
生活中,我们在吃鸡蛋等带壳的食物的时候,要先去壳;而在我们的数学中,解形如6x-3(x+2)=3这样带“壳”的方程的时候也要先去掉这层壳,方便我们“大快朵颐”,怎么来去“壳”呢?
例1:某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2 000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
提示:月平均用电量×n(月数)=n个月用电量
所有分量之和=总量
三、典型例题
下面我们通过实际的例子来详细学习“去壳”的过程
分析:若设上半年每月平均用电x度,
则下半年每月平均用电 度
上半年共用电 度,
下半年共用电 度.
因为全年共用了15万度电,
所以,可列方程_________________________.
(x-2000)
6(x-2000)
6x
6x+ 6(x-2000)=150000
三、典型例题
6x+6(x-2000)=150000
6x+6x-12000=150000
x=13500
去括号
合并同类项
移项
6x+6x=150000+12000
系数化为1
12x=162000
怎样解这个方程?
三、典型例题
去括号解一元一次方程的一般步骤及注意事项
步骤 注意事项
去括号 注意符号,防止漏乘;
移项 移项要变号,防止漏项;
合并同类项 系数为1或-1时,记得省略1;
系数化为1 方程两边都除以系数,分子、分母不要写倒了;
三、典型例题
例2:解方程
去括号,得2x-x-10=5x+2x-2
移项,得2x-x-5x-2x=-2+10
合并同类项,得-6x=8
系数化为1,得x=-4/3
解:
三、典型例题
3x-7(x-1)= 3-2(x+3).
解:去括号,得3x-7x+7=3-2x-6
移项,得3x-7x+2x=3-6-7
合并同类项,得-2x=-10
系数化为1,得x=5
2x-(x+10)=5x+2(x-1)
(1)6x=-2(3x-5)+10; (2)-2(x+5)=3(x-5)-6
1.解下列方程
解:
(1)6x=-2(3x-5)+10
6x=-6x+10+10
6x+6x=10+10
12x=20
(2)-2(x+5)=3(x-5)-6
-2x-10=3x-15-6
-2x-3x=-15-6+10
-5x=-11
【当堂检测】
三、典型例题
例3:一艘船从甲码头到乙码头顺流而行,用了2 h;从乙码头返回甲码头逆流而行,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的平均速度.
分析:我们知道这艘船往返路程不变.
顺流速度=船在静水中速度+水流速度
顺流时间=2 h
逆流速度=船在静水中速度-水流速度
逆流时间=2.5 h
等量关系:往返路程不变
解:设船在静水中的平均速度为x km/h,则顺流速度为(x+3)km/h,逆流速度为(x-3)km/h.
根据往返路程相等,可列方程:
2(x+3)=2.5(x-3).
去括号,得: 2x+6=2.5x-7.5.
移项及合并同类项,得: -0.5x=-13.5.
系数化,1,得: x=27.
答:船在静水中的平均速度为27 km/h.
三、典型例题
2. 某轮船从A码头到B码头顺水航行3小时,返航时用4.5小时,已知轮船在静水中的速度为4千米/小时,求水流速度为多少?
解:顺流航行的路程=逆流航行的路程;设水流速度为x千米/时,则顺流速度为 千米/时,逆流速度为 千米/时,
(x+4)
(4-x)
由题意得: 3(x+4)=4.5(4-x)
解之得: x=0.8.
答:水流速度为0.8千米/时.
【当堂检测】
3. 七年级170名学生参加植树活动,如果每个男生平均一天能挖树坑3个,每个女生平均一天能种树7棵,正好能使每个树坑种上一棵树,则该年级的男生,女生各有多少人?
解:设该年级男生有x人,则女生有(170-x)人.由题意得:
3x=7(170-x)
系数化为1: x=119
则女生为170-119=51(人)
答:男生有119人,女生有51人.
去括号: 3x=1190-7x
移项及合并: 10x=1190
【当堂检测】
本节课学习了什么?
1.解一元一次方程的步骤:
去括号 移项 合并同类项 系数化为1
(1)去括号法则:①去括号,看符号;②是“十”,不变号;③是“-”,全变号.
(2)括号前有因数时,不要漏乘如:2(x-3)= 2x-6
四、课堂总结
2.需要注意的是:
