第一章 有理数复习课课件(共38张PPT) 2023-2024学年人教版七年级数学上册
文档属性
| 名称 | 第一章 有理数复习课课件(共38张PPT) 2023-2024学年人教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 597.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 00:00:00 | ||
图片预览










文档简介
(共38张PPT)
第一章 有理数
复习课
学习导航
学习目标
知识结构
概念剖析
典型例题
当堂检测
课堂总结
1.会用正负数表示实际问题中的数,会用科学记数法表示数,会用
一、学习目标
数轴上的点表示有理数,并比较有理数的大小;
3.能进行有理数的加减、乘除、乘方的混合运算,并解决实际问题;
2.能借助数轴理解相反数和绝对值的意义,知道倒数的概念;
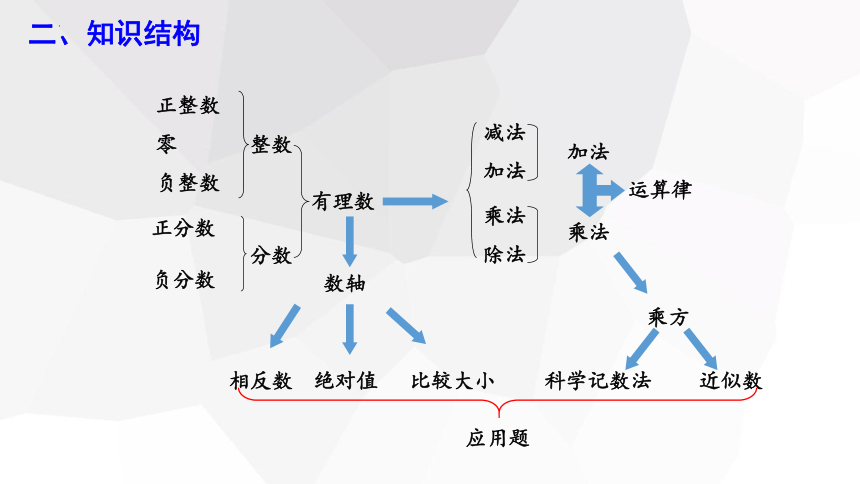
二、知识结构
有理数
整数
分数
正整数
零
负整数
正分数
负分数
数轴
相反数
绝对值
比较大小
减法
加法
乘法
除法
加法
乘法
运算律
乘方
科学记数法
应用题
近似数
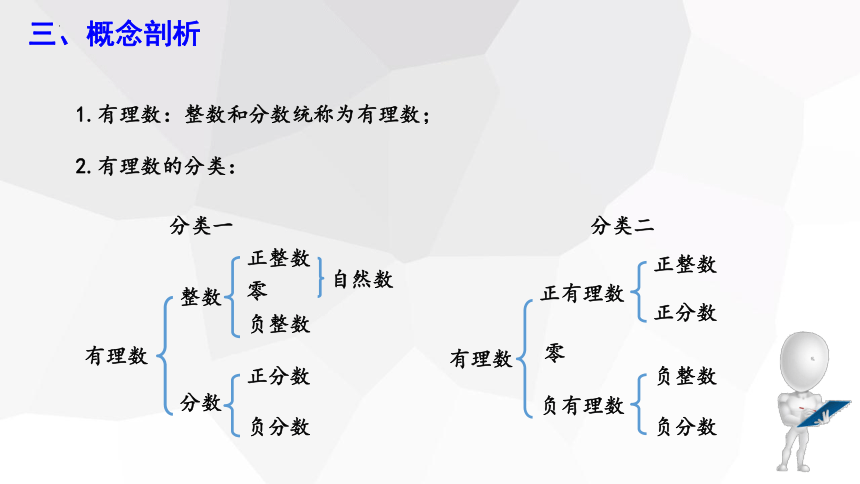
1.有理数:整数和分数统称为有理数;
2.有理数的分类:
三、概念剖析
有理数
整数
分数
零
正整数
负整数
正分数
负分数
自然数
分类一
有理数
正整数
正分数
零
正有理数
负有理数
负整数
负分数
分类二
三、概念剖析
3.数轴:规定了原点、正方向和单位长度的直线叫做数轴;
4.相反数:绝对值相同、符号相反的两个数互为相反数;零的相反数是零.
从数轴上看,表示互为相反数的两个点,分别在原点的两侧,
并到原点的距离相等.
三、概念剖析
即
从数轴上看,一个数的绝对值就是表示这个数的点到原点的
距离.因此,绝对值是一个非负数.
5.绝对值:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,
零的绝对值是零;
三、概念剖析
6. 有理数大小的比较:
方法1:正数都大于零,负数都小于零,正数大于 一切负数,
两个正数,绝对值大的数大,两个负数,绝对值大的反而小;
方法2:在数轴上表示的两个数,右边的数总比左边的数大.
三、概念剖析
7. 有理数的加减法:
有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数
的符号,并用较大的绝对值减去较小的绝对值
(3)互为相反数的两数相加,结果为0
(4)一个数同0相加,仍得这个数.
有理数的减法法则:减去一个数,等于加上这个数的相反数
三、概念剖析
倒数:乘积是1的两个数互为倒数.
8. 有理数的乘除法:
有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
有理数除法法则:除以一个不等于0的数,等于乘以这个数的倒数.
三、概念剖析
科学记数法:一般地,一个大于0的数可以写成a×10n的形式,其1≤a<10,
n为整数,这种记数法叫做科学记数法.
9. 有理数的乘方:
一般地,n个相同的因数a相乘,即a·a·a·…·a 记作an,读作a的n次方.
n个a
an中a叫做底数,n叫做指数,an看作是a的n次方结果时,也可以读作a的n次幂.
近似数:与实际相符的数叫做准确数,与实际相接近的数叫做近似数.
四、典型例题
(一)有理数的分类
例1.把下列各数填在相应的大括号内:
1,-0.1,-789,25,3.14,0,-20,-3.14,200%,
正整数集 { } 负整数集 { }
正分数集 { } 负分数集 { }
正有理数集{ }
负有理数集{ }
1、25、200%
-789、-20
-0.1,-3.14
-0.1、-789、-20、-3.14
3.14、
1、25、3.14、200%、
总结:有理数的分类分为两种.按定义分类分为整数和分数两大类,其中整
数又包括正整数、负整数和零,分数又包括正分数和负分数;
按性质符号分为正有理数、负有理数和零三大类,其中正有理数又包
括正整数和正分数,负有理数又包括负整数和负分数.
四、典型例题
【当堂检测】
1.下列各数:-6、1.9、0、-1、5.4、-2.2、+5、 、-1.9
其中正数有____个,负数有____个,正分数有____个,负
分数有____个,自然数有____个,整数有____个.
4
4
2
2
3
4
四、典型例题
(二)数轴
例2.在数轴上表示下列有理数:
3,-4, 4, 0,-6
0
2
4
6
-6
-4
-2
-4
4
3
-6
0
总结:一般地,设a是一个正数,则数轴上表示数a的点在原点的右边,与原
点的距离是a个单位长度;表示数-a的点在原点的左边,与原点的距
离是a个单位长度.
四、典型例题
【当堂检测】
2.如图,点M表示的数是9,那么点N表示的数是 .
0
M
N
-3
四、典型例题
(三)相反数
例3.-12的相反数是( )
A.12 B.-12 C.-21 D.
A
总结:(1)通常用a与-a表示一对相反数;
(2)a-b+c的相反数为-a+b-c;
(3)a与b互为相反数 a+b=0 ;
(4)互为相反数的两个数绝对值相等|-a|=|a|;
(5)|a|=|b| a=b或a=-b(a与b互为相反数).
四、典型例题
【当堂检测】
3.若-a=-6,则-a的相反数是 ,-(-3)的相反数是 .
6
-3
四、典型例题
(四)绝对值
例4.求以下各数的绝对值.12, , -7.5, 0.
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
总结:求一个数的绝对值,只要利用绝对值符号来表示一个数的
绝对值,然后再利用绝对值的性质进行化简即可.即“一添二去”.
(添绝对值符号,再去掉绝对值符号)
四、典型例题
【当堂检测】
4.填空
(1)若|a|=3,则a= , |a+1|=0,则a= ;
(2)若|a-5|+|b+3|=0,则a= ,b= ;
(3)若|x+2|+|y-2|=0,则x= ,y= .
±3
-1
5
-3
-2
2
四、典型例题
(五)有理数加减法
例5.计算
(1)(-3)+(-9)+6+(-1) (2)(-5)-(-8)-(-3)
解:(1)(-3)+(-9)+6+(-1)
=(-12)+6+(-1)
=(-6)+(-1)
=-7
(2)(-5)-(-8)-(-3)
=3-(-3)
=6
四、典型例题
例6.计算(-0.5)-(-3)+2.5-7.5 .
解:原式=-0.5+3+2.5+(-7.5)
=2.5+2.5+(-7.5)
=5+(-7.5)
=-2.5
(五)有理数加减法
总结:有理数加减混合运算首先要将式中的减法转化为加法,再运用
有理数的加法运算律进行运算.
四、典型例题
【当堂检测】
5.某公交车上原有乘客22人,经过4个站点时上下车情况如下(上车为正、下车为负)(-6,+3),(-5,+4),(-3,+1),(-4,+1),问此时车上还有多少乘客?
解:根据题意列出式子:22+(-6)+3+(-5)+4+(-3)+1+(-4)+1=13人
答:此时车上还有乘客13人.
四、典型例题
(六)有理数的乘除法
例7.计算( ) ×( )÷( )÷2
解:原式=
( )×( )×( )×
=( )× ×( )×( )
=
四、典型例题
(六)有理数的乘除法
例8.计算(-3)×[(-5)+9]÷2
解:原式= (-3)×[(-5)+9]÷2
=(-3)×4÷2
=(-12)÷2
=-6
总结:有理数的加减乘除混合运算,如无括号指出先做什么运算,
则按照“先乘除,后加减”的顺序进行.
四、典型例题
【当堂检测】
6.计算9÷3×(-5)-6÷( - )
解:原式
【当堂检测】
7.计算:[(-4)×( )÷( )+(-3)×( )]×(-2)+(-6)
解:原式=( - )×(-2)+(-6)
=(-9)×(-2)+(-6)
=18+(-6)
=12
四、典型例题
(七)有理数的乘方
例9.计算 4×(-2)3 -3 ×(-1)+13
解:原式=4×(-8)-(-3)+13
= -32+3+13
= -16
四、典型例题
(七)有理数的乘方
例10.用科学记数法表示下列各数
(1)330000 (2)463.56
解:(1)3.3×105 (2)4.6356×102
总结:1.进行有理数混合运算时:先乘方,再乘除,最后加减
2.用科学记数法a×10n表示大数需要注意两点:一是1≤a<10;
二是当大数是大于10的整数时,n为整数位数减去1.
3.求一个数的近似数,用四舍五入法,要求精确到哪一位就四
舍五入到哪一位.
四、典型例题
【当堂检测】
8.计算(-6)3 +[22 -(1+32)×5]
解:原式=(-216)+(4-10×5)
=(-216)+(-46)
= -262
【当堂检测】
9.将3.141×108精确到万位.
解:3.141×108 = 3.1410×108
五、课堂总结
有理数
整数
分数
正整数
零
负整数
正分数
负分数
数轴
相反数
绝对值
比较大小
减法
加法
乘法
除法
加法
乘法
运算律
乘方
科学记数法
应用题
近似数
第一章 有理数
复习课
学习导航
学习目标
知识结构
概念剖析
典型例题
当堂检测
课堂总结
1.会用正负数表示实际问题中的数,会用科学记数法表示数,会用
一、学习目标
数轴上的点表示有理数,并比较有理数的大小;
3.能进行有理数的加减、乘除、乘方的混合运算,并解决实际问题;
2.能借助数轴理解相反数和绝对值的意义,知道倒数的概念;
二、知识结构
有理数
整数
分数
正整数
零
负整数
正分数
负分数
数轴
相反数
绝对值
比较大小
减法
加法
乘法
除法
加法
乘法
运算律
乘方
科学记数法
应用题
近似数
1.有理数:整数和分数统称为有理数;
2.有理数的分类:
三、概念剖析
有理数
整数
分数
零
正整数
负整数
正分数
负分数
自然数
分类一
有理数
正整数
正分数
零
正有理数
负有理数
负整数
负分数
分类二
三、概念剖析
3.数轴:规定了原点、正方向和单位长度的直线叫做数轴;
4.相反数:绝对值相同、符号相反的两个数互为相反数;零的相反数是零.
从数轴上看,表示互为相反数的两个点,分别在原点的两侧,
并到原点的距离相等.
三、概念剖析
即
从数轴上看,一个数的绝对值就是表示这个数的点到原点的
距离.因此,绝对值是一个非负数.
5.绝对值:一个正数的绝对值是它本身,一个负数的绝对值是它的相反数,
零的绝对值是零;
三、概念剖析
6. 有理数大小的比较:
方法1:正数都大于零,负数都小于零,正数大于 一切负数,
两个正数,绝对值大的数大,两个负数,绝对值大的反而小;
方法2:在数轴上表示的两个数,右边的数总比左边的数大.
三、概念剖析
7. 有理数的加减法:
有理数的加法法则:
(1)同号两数相加,取相同的符号,并把绝对值相加;
(2)绝对值不相等的异号两数相加,取绝对值较大的加数
的符号,并用较大的绝对值减去较小的绝对值
(3)互为相反数的两数相加,结果为0
(4)一个数同0相加,仍得这个数.
有理数的减法法则:减去一个数,等于加上这个数的相反数
三、概念剖析
倒数:乘积是1的两个数互为倒数.
8. 有理数的乘除法:
有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数同0相乘,都得0.
有理数除法法则:除以一个不等于0的数,等于乘以这个数的倒数.
三、概念剖析
科学记数法:一般地,一个大于0的数可以写成a×10n的形式,其1≤a<10,
n为整数,这种记数法叫做科学记数法.
9. 有理数的乘方:
一般地,n个相同的因数a相乘,即a·a·a·…·a 记作an,读作a的n次方.
n个a
an中a叫做底数,n叫做指数,an看作是a的n次方结果时,也可以读作a的n次幂.
近似数:与实际相符的数叫做准确数,与实际相接近的数叫做近似数.
四、典型例题
(一)有理数的分类
例1.把下列各数填在相应的大括号内:
1,-0.1,-789,25,3.14,0,-20,-3.14,200%,
正整数集 { } 负整数集 { }
正分数集 { } 负分数集 { }
正有理数集{ }
负有理数集{ }
1、25、200%
-789、-20
-0.1,-3.14
-0.1、-789、-20、-3.14
3.14、
1、25、3.14、200%、
总结:有理数的分类分为两种.按定义分类分为整数和分数两大类,其中整
数又包括正整数、负整数和零,分数又包括正分数和负分数;
按性质符号分为正有理数、负有理数和零三大类,其中正有理数又包
括正整数和正分数,负有理数又包括负整数和负分数.
四、典型例题
【当堂检测】
1.下列各数:-6、1.9、0、-1、5.4、-2.2、+5、 、-1.9
其中正数有____个,负数有____个,正分数有____个,负
分数有____个,自然数有____个,整数有____个.
4
4
2
2
3
4
四、典型例题
(二)数轴
例2.在数轴上表示下列有理数:
3,-4, 4, 0,-6
0
2
4
6
-6
-4
-2
-4
4
3
-6
0
总结:一般地,设a是一个正数,则数轴上表示数a的点在原点的右边,与原
点的距离是a个单位长度;表示数-a的点在原点的左边,与原点的距
离是a个单位长度.
四、典型例题
【当堂检测】
2.如图,点M表示的数是9,那么点N表示的数是 .
0
M
N
-3
四、典型例题
(三)相反数
例3.-12的相反数是( )
A.12 B.-12 C.-21 D.
A
总结:(1)通常用a与-a表示一对相反数;
(2)a-b+c的相反数为-a+b-c;
(3)a与b互为相反数 a+b=0 ;
(4)互为相反数的两个数绝对值相等|-a|=|a|;
(5)|a|=|b| a=b或a=-b(a与b互为相反数).
四、典型例题
【当堂检测】
3.若-a=-6,则-a的相反数是 ,-(-3)的相反数是 .
6
-3
四、典型例题
(四)绝对值
例4.求以下各数的绝对值.12, , -7.5, 0.
解:
|12|=12;
| |= ;
|-7.5|=7.5;
|0|=0.
总结:求一个数的绝对值,只要利用绝对值符号来表示一个数的
绝对值,然后再利用绝对值的性质进行化简即可.即“一添二去”.
(添绝对值符号,再去掉绝对值符号)
四、典型例题
【当堂检测】
4.填空
(1)若|a|=3,则a= , |a+1|=0,则a= ;
(2)若|a-5|+|b+3|=0,则a= ,b= ;
(3)若|x+2|+|y-2|=0,则x= ,y= .
±3
-1
5
-3
-2
2
四、典型例题
(五)有理数加减法
例5.计算
(1)(-3)+(-9)+6+(-1) (2)(-5)-(-8)-(-3)
解:(1)(-3)+(-9)+6+(-1)
=(-12)+6+(-1)
=(-6)+(-1)
=-7
(2)(-5)-(-8)-(-3)
=3-(-3)
=6
四、典型例题
例6.计算(-0.5)-(-3)+2.5-7.5 .
解:原式=-0.5+3+2.5+(-7.5)
=2.5+2.5+(-7.5)
=5+(-7.5)
=-2.5
(五)有理数加减法
总结:有理数加减混合运算首先要将式中的减法转化为加法,再运用
有理数的加法运算律进行运算.
四、典型例题
【当堂检测】
5.某公交车上原有乘客22人,经过4个站点时上下车情况如下(上车为正、下车为负)(-6,+3),(-5,+4),(-3,+1),(-4,+1),问此时车上还有多少乘客?
解:根据题意列出式子:22+(-6)+3+(-5)+4+(-3)+1+(-4)+1=13人
答:此时车上还有乘客13人.
四、典型例题
(六)有理数的乘除法
例7.计算( ) ×( )÷( )÷2
解:原式=
( )×( )×( )×
=( )× ×( )×( )
=
四、典型例题
(六)有理数的乘除法
例8.计算(-3)×[(-5)+9]÷2
解:原式= (-3)×[(-5)+9]÷2
=(-3)×4÷2
=(-12)÷2
=-6
总结:有理数的加减乘除混合运算,如无括号指出先做什么运算,
则按照“先乘除,后加减”的顺序进行.
四、典型例题
【当堂检测】
6.计算9÷3×(-5)-6÷( - )
解:原式
【当堂检测】
7.计算:[(-4)×( )÷( )+(-3)×( )]×(-2)+(-6)
解:原式=( - )×(-2)+(-6)
=(-9)×(-2)+(-6)
=18+(-6)
=12
四、典型例题
(七)有理数的乘方
例9.计算 4×(-2)3 -3 ×(-1)+13
解:原式=4×(-8)-(-3)+13
= -32+3+13
= -16
四、典型例题
(七)有理数的乘方
例10.用科学记数法表示下列各数
(1)330000 (2)463.56
解:(1)3.3×105 (2)4.6356×102
总结:1.进行有理数混合运算时:先乘方,再乘除,最后加减
2.用科学记数法a×10n表示大数需要注意两点:一是1≤a<10;
二是当大数是大于10的整数时,n为整数位数减去1.
3.求一个数的近似数,用四舍五入法,要求精确到哪一位就四
舍五入到哪一位.
四、典型例题
【当堂检测】
8.计算(-6)3 +[22 -(1+32)×5]
解:原式=(-216)+(4-10×5)
=(-216)+(-46)
= -262
【当堂检测】
9.将3.141×108精确到万位.
解:3.141×108 = 3.1410×108
五、课堂总结
有理数
整数
分数
正整数
零
负整数
正分数
负分数
数轴
相反数
绝对值
比较大小
减法
加法
乘法
除法
加法
乘法
运算律
乘方
科学记数法
应用题
近似数
