18.2.3正方形课件
图片预览




文档简介
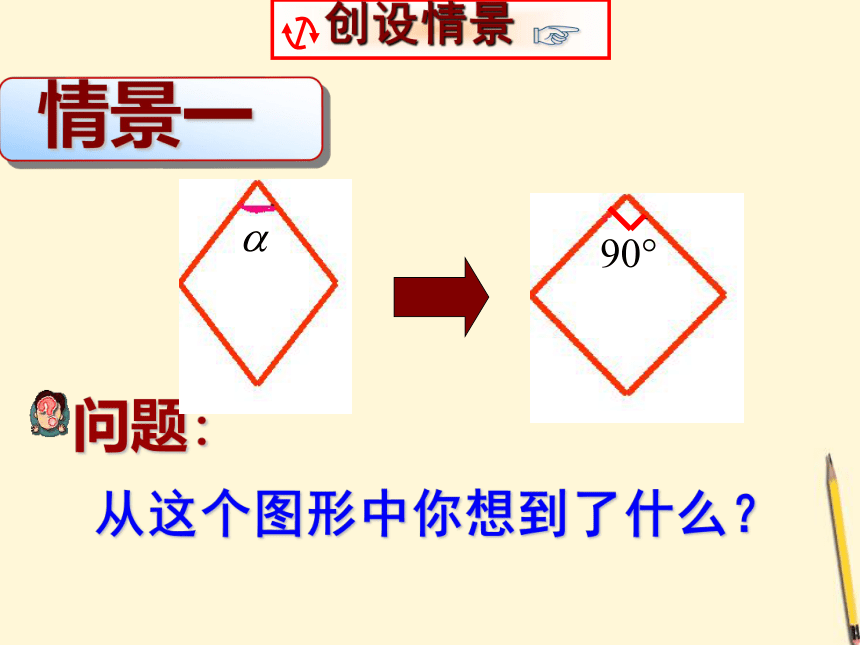
课件39张PPT。 正方形的定义及性质情景一新知探究情景一新知探究情景一新知探究 创设情景?问题: 从这个图形中你想到了什么?
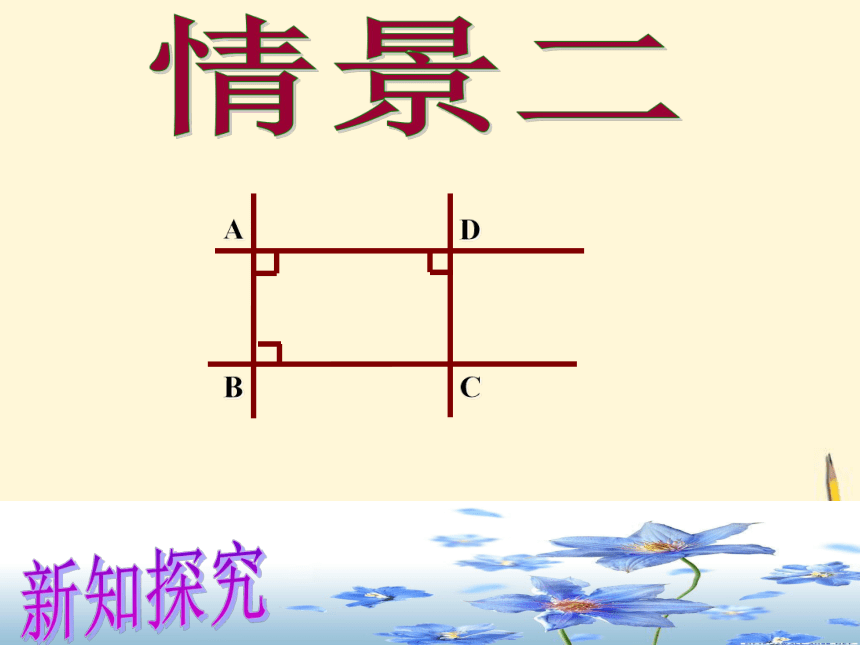
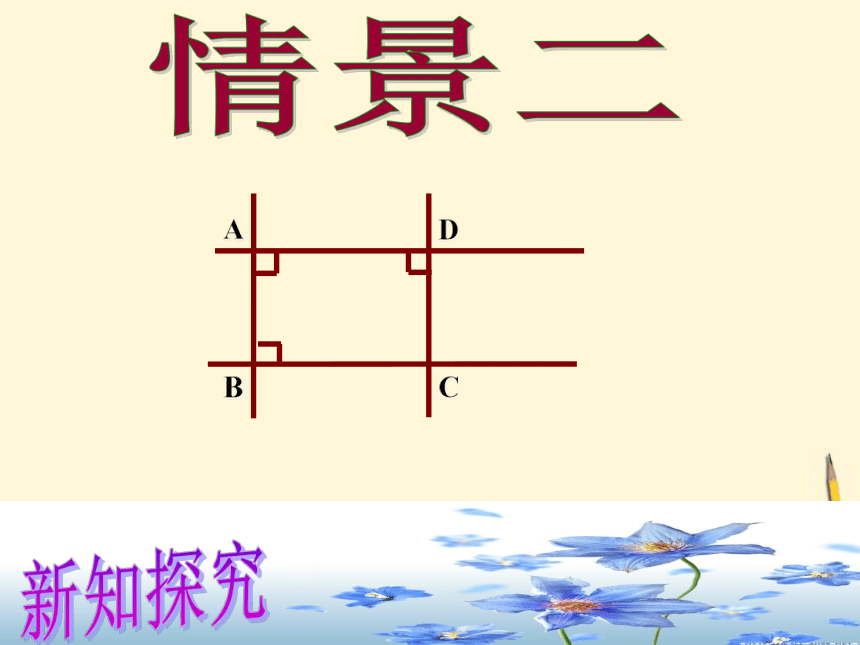
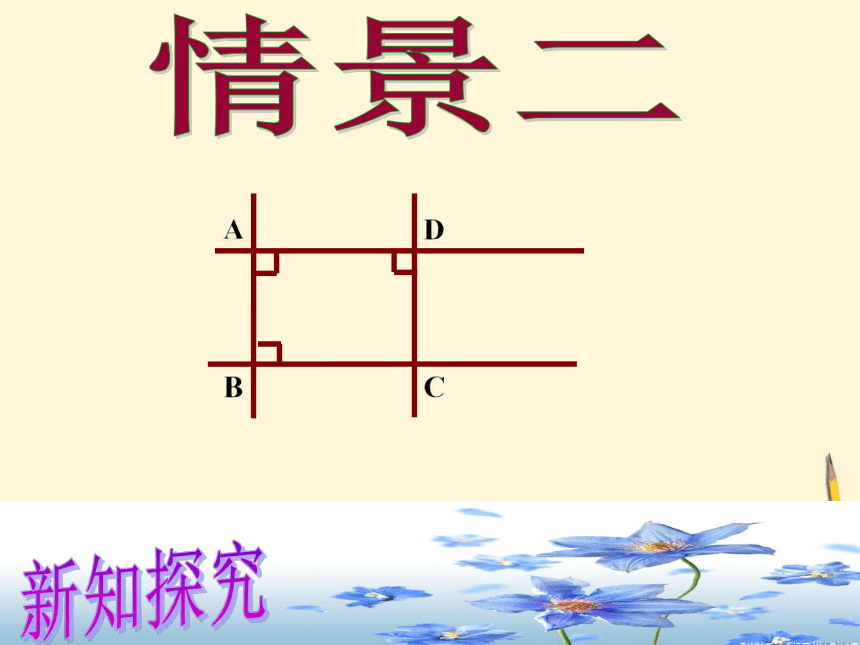
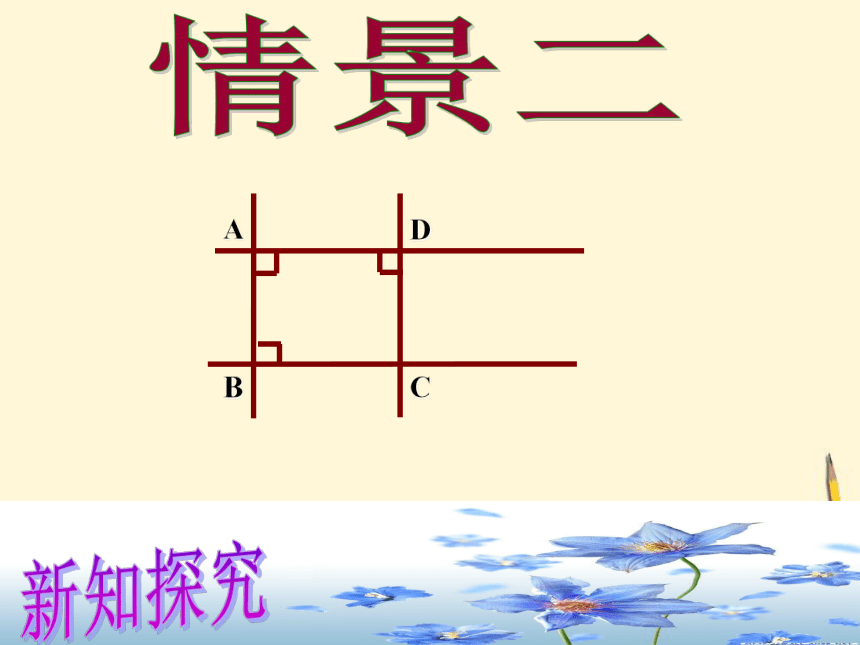
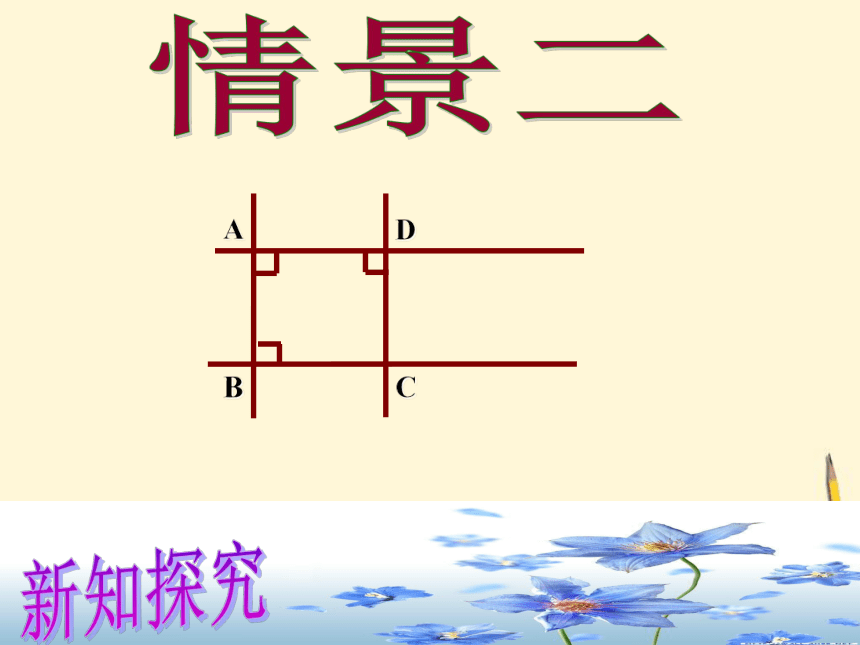
ABCD情景二新知探究ABCD情景二新知探究ABCD情景二新知探究AB情景二新知探究AB情景二新知探究AB情景二新知探究AB情景二新知探究ABCD情景二新知探究ABCDAB邻边相等的矩形想一想:正方形是怎样的矩形?矩形正方形新知探究菱形正方形一个角是直角的菱形想一想:正方形是怎样的菱形?新知探究有一个角是直角有一组邻边相等回忆如何给正方形下定义?给正方形下个定义
_______________________________ 的平行四边形是正方形。_______________的菱形是正方形。_________________的矩形是正方形。有一组邻边相等且有一个角是直角有一个角是直角有一组邻边相等正方形的定义:平行四边形矩形菱形正方形对称性特征 也是中心对称图形,对称中心为点O它是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角有人说正方形是一个完美的图形,为什呢?回顾平行四边形,矩形,菱形的性质,完成表格前三列对边平行且相等四条边相等对边平行且四条边相等对角相等四个角都是直角四个角都是直角对角线互相平分对角线相等对角线互相垂直,每条对角线平分一组对角对角线相等且互相垂直平分,每条对角线平分一组对角中心对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形图形性质分类正方形类
比
归
纳√(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )快速反应判断题:(2)正方形一定是矩形.( )
(3)正方形一定是菱形.( )
(4)菱形一定是正方形.( )
(5)矩形一定是正方形.( )
(6)正方形、矩形、菱形都是平行四边形. ( )√√√×××(7)正方形是轴对称图形,一共有2条对称轴( )正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD选择题:1、如图:正方形ABCD的周长为15cm,则矩形EFCG的周长为 cm。 7.5练一练 2.已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______. 练一练2246363.已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=______, 例1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.已知:四边形ABCD是矩形,对角线AC、BD相交于点O.求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.证明:∵四边形ABCD是正方形并且△ABO≌△BCO≌△CDO≌△DAO∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形,∴AC=BD,AC⊥BD,AO=CO=BO=DO. 例2、如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有:例2、如图,正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:∴OA-OM=OB-ON∴OM=ON∴∠OMN=∠1=∠3=∠ONM=45°又∵MN∥AB∠1=∠2=∠3=45°∴OA=OB AB=BC∵四边形ABCD是正方形即:AM=BN∴△ABM≌△BCN∴BM=CN3、已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF3、已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°证明:∴DM=DF∴Rt△CDM≌Rt△ADF (AAS)又∵CD=AD,∠ADF=∠MDC=Rt∠∴∠1=∠2∵∠CMD=∠AME∴∠ADC=∠AEM=90°∵CE⊥AF 四边形ABCD是正方形∴∠MFD=45°4、如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB (2) BH⊥AF 5、如图,已知正方形ABCD,延长AB到E,作AG⊥EC于G,AG交BC于F,
求证:AF=CE。 12补充练习:
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC= cm,求正方形DEFG的边长. 3、如图4-54,正方形ABCD,AB=4a,M为AB的中点,ED=3AE。
(1)求ME的长。
(2)求证△EMC为直角三角形。 4、已知:如图4-53,点A'、B'、C'、D'分别是正方形ABCD四条边上的点,并且AA'=BB'=CC'=DD'。
求证:四边形A‘B’C‘D’是正方形 5.如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 6、已知正方形ABCD的边长为4,E为BC边上一点,且BE=1,P为AC上一点,求PE+PB的最小值.
7、在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想。
ABCD情景二新知探究ABCD情景二新知探究ABCD情景二新知探究AB情景二新知探究AB情景二新知探究AB情景二新知探究AB情景二新知探究ABCD情景二新知探究ABCDAB邻边相等的矩形想一想:正方形是怎样的矩形?矩形正方形新知探究菱形正方形一个角是直角的菱形想一想:正方形是怎样的菱形?新知探究有一个角是直角有一组邻边相等回忆如何给正方形下定义?给正方形下个定义
_______________________________ 的平行四边形是正方形。_______________的菱形是正方形。_________________的矩形是正方形。有一组邻边相等且有一个角是直角有一个角是直角有一组邻边相等正方形的定义:平行四边形矩形菱形正方形对称性特征 也是中心对称图形,对称中心为点O它是轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,两组对角相等,对角线互相平分(2)具有矩形的一切性质四个角都是直角,对角线相等(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角有人说正方形是一个完美的图形,为什呢?回顾平行四边形,矩形,菱形的性质,完成表格前三列对边平行且相等四条边相等对边平行且四条边相等对角相等四个角都是直角四个角都是直角对角线互相平分对角线相等对角线互相垂直,每条对角线平分一组对角对角线相等且互相垂直平分,每条对角线平分一组对角中心对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形既是中心对称图形又是轴对称图形图形性质分类正方形类
比
归
纳√(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形( )快速反应判断题:(2)正方形一定是矩形.( )
(3)正方形一定是菱形.( )
(4)菱形一定是正方形.( )
(5)矩形一定是正方形.( )
(6)正方形、矩形、菱形都是平行四边形. ( )√√√×××(7)正方形是轴对称图形,一共有2条对称轴( )正方形具有而矩形不一定具有的性质是( )
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.2.正方形具有而菱形不一定具有的性质( )
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等. BD选择题:1、如图:正方形ABCD的周长为15cm,则矩形EFCG的周长为 cm。 7.5练一练 2.已知:正方形ABCD对角线AC、BD相 交于点O,且AB=2cm,则AC= ,
正方形的面积S=______. 练一练2246363.已知:在正方形ABCD中,对角线AC、
BD相交于点O,且AC=6 cm,
面积S=________.则边长AB=______, 例1.求证:正方形的两条对角线把正方形分成四个全等的等腰直角三角形.已知:四边形ABCD是矩形,对角线AC、BD相交于点O.求证:△ABO、△BCO、△CDO、△DAO是全等的等腰直角三角形.证明:∵四边形ABCD是正方形并且△ABO≌△BCO≌△CDO≌△DAO∴ △ABO、△BCO、△CDO、△DAO都是等腰直角三角形,∴AC=BD,AC⊥BD,AO=CO=BO=DO. 例2、如图(3),正方形ABCD中,AC、BD相交于O,
分析:要证明BM=CN,大家观察
图形可以考虑证哪两个三角形全等 ?
MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。
你能完成证明吗???
AB=BC,∠1=∠2=45 ° 条件够吗? 还需要的条件是 AM=BN
△ABM≌△BCN
你所要证明的两个三角形已经满足
了哪些条件?
由正方形可以得到的条件有:例2、如图,正方形ABCD中,AC、BD相交于O,MN∥AB且MN分别交OA、OB于M、N,求证:BM=CN。 证明:∴OA-OM=OB-ON∴OM=ON∴∠OMN=∠1=∠3=∠ONM=45°又∵MN∥AB∠1=∠2=∠3=45°∴OA=OB AB=BC∵四边形ABCD是正方形即:AM=BN∴△ABM≌△BCN∴BM=CN3、已知:如图(4)在正方形ABCD中,F为CD延长线
上一点,CE⊥AF于E,交AD于M,
求证:∠MFD=45° 分析:
欲证∠MFD=45°,由于
△MDF是直角三角形,只须证△MDF是等腰三角形,即只要证 _____=_____要证MD=FD,大家只须证得哪两个三角形全等?
试一试
看能不能完成证明???△CMD≌△ADF3、已知:如图(4)在正方形ABCD中,F为CD延长线上一点,CE⊥AF于E,交AD于M, 求证:∠MFD=45°证明:∴DM=DF∴Rt△CDM≌Rt△ADF (AAS)又∵CD=AD,∠ADF=∠MDC=Rt∠∴∠1=∠2∵∠CMD=∠AME∴∠ADC=∠AEM=90°∵CE⊥AF 四边形ABCD是正方形∴∠MFD=45°4、如图,在AB上取一点C,以AC、BC为正方形的一边在同一侧作正方形AEDC和BCFG连结AF、BD延长BD交AF于H。 求证:(1) △ACF≌△DCB (2) BH⊥AF 5、如图,已知正方形ABCD,延长AB到E,作AG⊥EC于G,AG交BC于F,
求证:AF=CE。 12补充练习:
1、如图,正方形ABCD的边长为4cm,则图中阴影部分的面积为 平方厘米.2、如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E、F在边AB上,点G在边BC上.
(1)求证AE=BF;
(2)若BC= cm,求正方形DEFG的边长. 3、如图4-54,正方形ABCD,AB=4a,M为AB的中点,ED=3AE。
(1)求ME的长。
(2)求证△EMC为直角三角形。 4、已知:如图4-53,点A'、B'、C'、D'分别是正方形ABCD四条边上的点,并且AA'=BB'=CC'=DD'。
求证:四边形A‘B’C‘D’是正方形 5.如图,△ABC的外面作正方形ABDE和ACFG,连结BG、CE,交点为N。 求证:∠CEA=∠ABG 6、已知正方形ABCD的边长为4,E为BC边上一点,且BE=1,P为AC上一点,求PE+PB的最小值.
7、在正方形ABCD中,AC是对角线,AE平分∠BAC,试猜想AB、AC、BE之间的关系,并证明你的猜想。
