1.2.1充分条件与必要条件(广东省茂名市)
文档属性
| 名称 | 1.2.1充分条件与必要条件(广东省茂名市) |  | |
| 格式 | rar | ||
| 文件大小 | 339.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-05 23:51:00 | ||
图片预览




文档简介
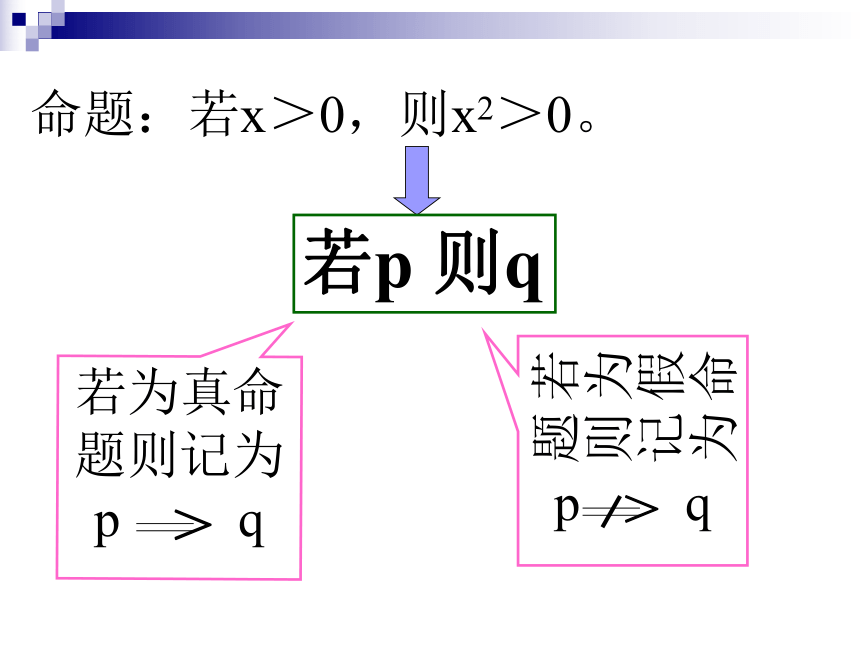
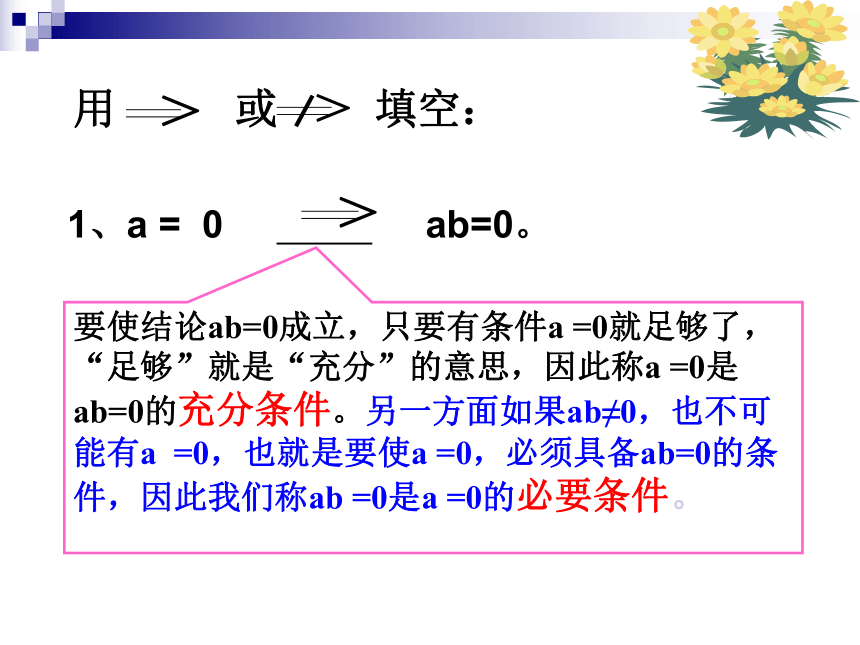
课件15张PPT。1.2 充分条件与必要条件命题:若x>0,则x2>0。若p 则q 1、a = 0 ab=0。
2、ab =0 a =0。
3、两个角相等 两个角是对顶角。
4、两个角是对顶角 两个角相等。要使结论ab=0成立,只要有条件a =0就足够了,“足够”就是“充分”的意思,因此称a =0是ab=0的充分条件。另一方面如果ab≠0,也不可能有a =0,也就是要使a =0,必须具备ab=0的条件,因此我们称ab =0是a =0的必要条件。
则“x > a2 + b2” 是“x > 2ab”的充分条件,例如:(1)由x>0则“x>0”是 “x2>0”的充分条件, x2>0,(2) 若x > a2 + b2x > 2ab “x > 2ab”是“x > a2 + b2”的必要条件。 “x2>0”是 “x>0”的必要条件;例1 下列“若p,则q”形式的命题中,哪些命题中
的p是q的充分条件?
(1)若x=1,则x2-4x+3 =0;
(2)若f(x)=x,则f(x)为增函数;
(3)若x为无理数,则x2为无理数。例2 下列“若p,则q”形式的命题中,哪些命题中的
q 是p的必要条件?
(1)若x=y,则x2 =y2;
(2)若两个三角形全等,则这两个三角形的面积相等;
(3)若a>b,则ac>bc。是是否是是否课堂练习: 2、填空:
(1)“a、b是偶数”是“a+b是偶数”的 。
(2) “ab>0”是“a、b都是负数”的 。
(3)“两个三角形的面积相等”是“这两个三角
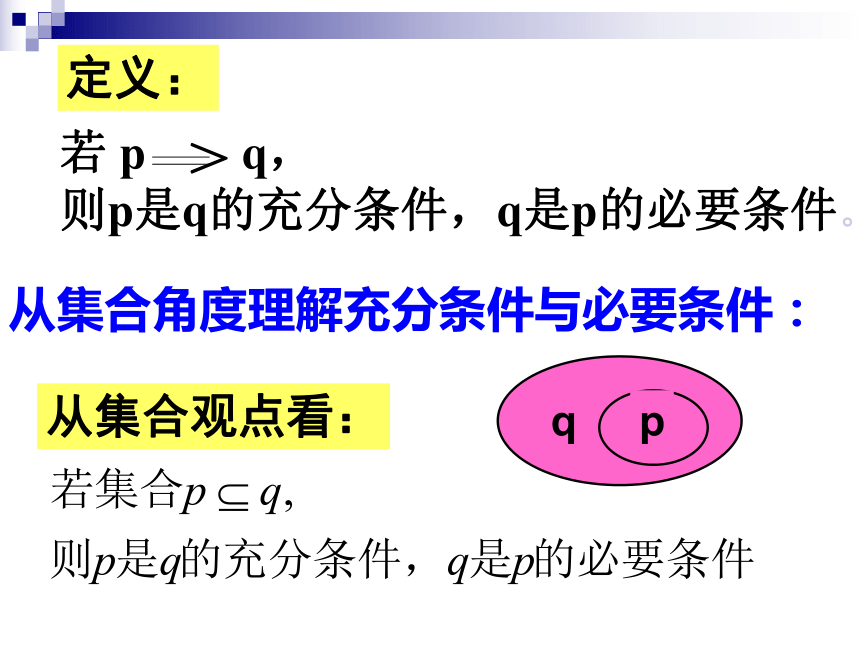
形全等”的 。 充分条件必要条件必要条件1、课本:P10从集合角度理解充分条件与必要条件:从集合观点看:思考?已知 p: 整数a是6的倍数
q: 整数a是2和3的倍数
那么: p是 q的什么条件? q 又是p的什么条件?-----① p q:p是q的充分条件,q是p的必要条件② q p :q是p的充分条件,p是q 的必要条件由① ② 得: p q也就是说: p是q 的充要条件, q是p的充要条件.即: p与q互为充要条件例3 : 下列各题中,哪些p是q的充要条件?
(1)p: b=0,q: 函数f(x)=ax2+bx+c 是偶函数;
(2) p: x>0,y>0, q: xy>0 ;
(3) p: a>b, q: a+c>b+c.练习:判断下列命题中,哪些 p是 q的充要
条件? p q
(1)x2>1 x< -1
(2)|x-2|<3 - x2 +4x+5 >0
(3)A=B sinA=sinB
(4)a=2 直线ax+2y=0平行于直线x+y=1
是否否是充分条件、必要条件和充要条件的联系与区别: 1、从定义上看:(1)若p q, 但q p,(2)若q p, 但p q,(3)若p q, 但q p,(4)若p q, 但q p,则p是q的充分不必要条件则p是q的必要不充分条件 则p是q的充要条件 则p是q的 既不充分也不
必要条件小结:2、从集合与集合之间的关系上看:若命题p、q分别以集合A、B的形式出现,则:(1)若A B,(2)若B A ,(3)若A = B ,(4)若A B ,且 B A ,则p是q的充分不必要条件则p是q的必要不充分条件 则p是q的充要条件 则p是q的既不充分也 不必要条件判别充要条件问题的:1、步骤 :(1)认清条件和结论。(2)考察 p q和q p的真假。2、判别的技巧:(1)可先简化命题。(2)否定一个命题只要举出一个反例即可。 (3)将命题转化为等价的逆否命题后再判断。
2、ab =0 a =0。
3、两个角相等 两个角是对顶角。
4、两个角是对顶角 两个角相等。要使结论ab=0成立,只要有条件a =0就足够了,“足够”就是“充分”的意思,因此称a =0是ab=0的充分条件。另一方面如果ab≠0,也不可能有a =0,也就是要使a =0,必须具备ab=0的条件,因此我们称ab =0是a =0的必要条件。
则“x > a2 + b2” 是“x > 2ab”的充分条件,例如:(1)由x>0则“x>0”是 “x2>0”的充分条件, x2>0,(2) 若x > a2 + b2x > 2ab “x > 2ab”是“x > a2 + b2”的必要条件。 “x2>0”是 “x>0”的必要条件;例1 下列“若p,则q”形式的命题中,哪些命题中
的p是q的充分条件?
(1)若x=1,则x2-4x+3 =0;
(2)若f(x)=x,则f(x)为增函数;
(3)若x为无理数,则x2为无理数。例2 下列“若p,则q”形式的命题中,哪些命题中的
q 是p的必要条件?
(1)若x=y,则x2 =y2;
(2)若两个三角形全等,则这两个三角形的面积相等;
(3)若a>b,则ac>bc。是是否是是否课堂练习: 2、填空:
(1)“a、b是偶数”是“a+b是偶数”的 。
(2) “ab>0”是“a、b都是负数”的 。
(3)“两个三角形的面积相等”是“这两个三角
形全等”的 。 充分条件必要条件必要条件1、课本:P10从集合角度理解充分条件与必要条件:从集合观点看:思考?已知 p: 整数a是6的倍数
q: 整数a是2和3的倍数
那么: p是 q的什么条件? q 又是p的什么条件?-----① p q:p是q的充分条件,q是p的必要条件② q p :q是p的充分条件,p是q 的必要条件由① ② 得: p q也就是说: p是q 的充要条件, q是p的充要条件.即: p与q互为充要条件例3 : 下列各题中,哪些p是q的充要条件?
(1)p: b=0,q: 函数f(x)=ax2+bx+c 是偶函数;
(2) p: x>0,y>0, q: xy>0 ;
(3) p: a>b, q: a+c>b+c.练习:判断下列命题中,哪些 p是 q的充要
条件? p q
(1)x2>1 x< -1
(2)|x-2|<3 - x2 +4x+5 >0
(3)A=B sinA=sinB
(4)a=2 直线ax+2y=0平行于直线x+y=1
是否否是充分条件、必要条件和充要条件的联系与区别: 1、从定义上看:(1)若p q, 但q p,(2)若q p, 但p q,(3)若p q, 但q p,(4)若p q, 但q p,则p是q的充分不必要条件则p是q的必要不充分条件 则p是q的充要条件 则p是q的 既不充分也不
必要条件小结:2、从集合与集合之间的关系上看:若命题p、q分别以集合A、B的形式出现,则:(1)若A B,(2)若B A ,(3)若A = B ,(4)若A B ,且 B A ,则p是q的充分不必要条件则p是q的必要不充分条件 则p是q的充要条件 则p是q的既不充分也 不必要条件判别充要条件问题的:1、步骤 :(1)认清条件和结论。(2)考察 p q和q p的真假。2、判别的技巧:(1)可先简化命题。(2)否定一个命题只要举出一个反例即可。 (3)将命题转化为等价的逆否命题后再判断。
