等腰三角形(2)(辽宁省鞍山市)
文档属性
| 名称 | 等腰三角形(2)(辽宁省鞍山市) |  | |
| 格式 | rar | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-10-07 20:31:00 | ||
图片预览



文档简介
课件12张PPT。 东汉末年,吴、蜀、魏三分天下,吴国与蜀国
曾联合攻打魏国。如图所示,(蜀国沿BA行进,
吴国沿CA行进)当时测得∠B= ∠C,
如果蜀、吴军队以同样的速度同时出发,能不能大约同时赶
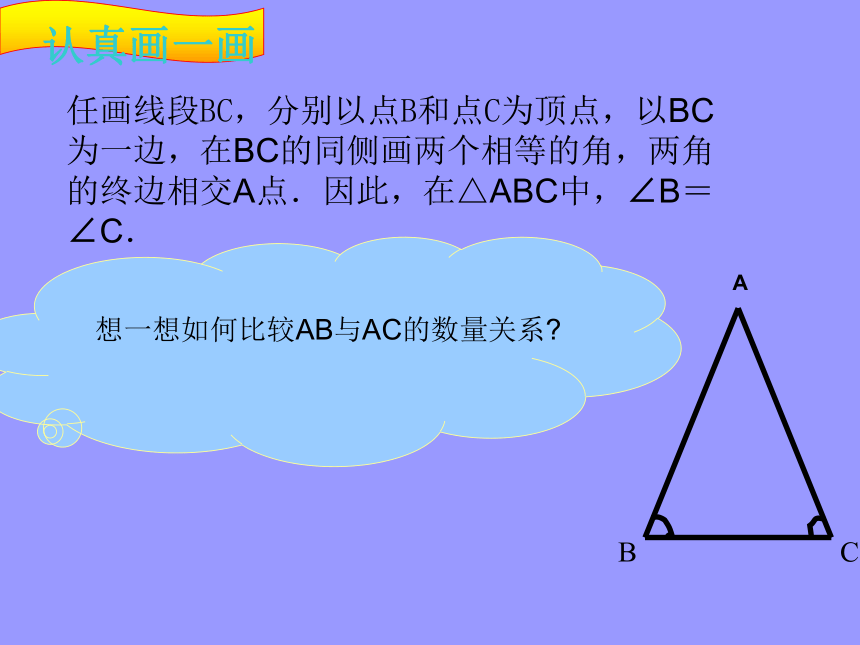
到魏国进行袭击?对于一个三角形,如果有两个角相等,那么它们所对的边有什么关系?一、问题情境BCA任画线段BC,分别以点B和点C为顶点,以BC为一边,在BC的同侧画两个相等的角,两角的终边相交A点.因此,在△ABC中,∠B=∠C.想一想如何比较AB与AC的数量关系?
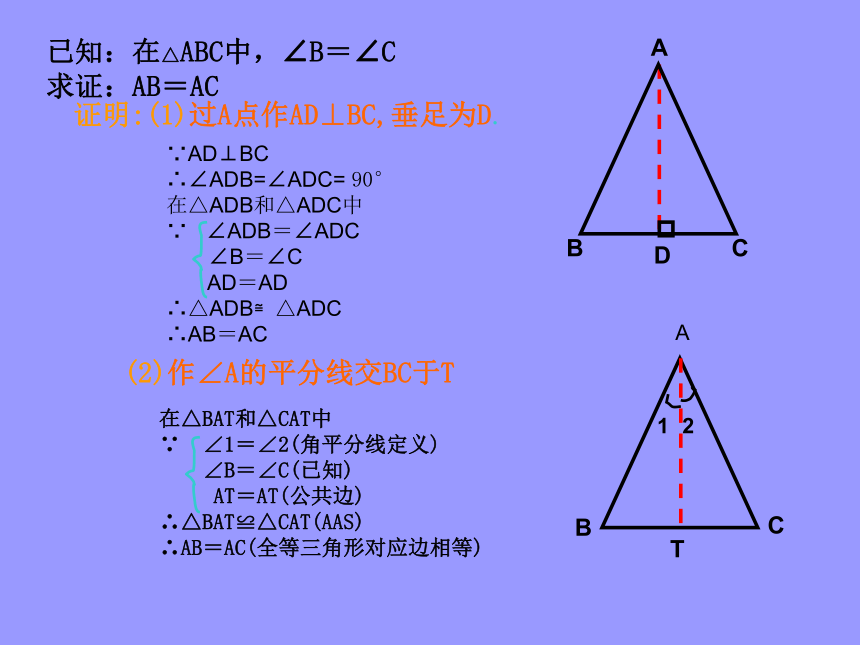
已知:在△ABC中,∠B=∠C 求证:AB=AC (2)作∠A的平分线交BC于TABCT在△BAT和△CAT中
∵ ∠1=∠2(角平分线定义)
∠B=∠C(已知)
AT=AT(公共边)
∴△BAT≌△CAT(AAS)
∴AB=AC(全等三角形对应边相等)证明:(1)过A点作AD⊥BC,垂足为D.ABCD∵AD⊥BC
∴∠ADB=∠ADC= 90°
在△ADB和△ADC中
∵ ∠ADB=∠ADC
∠B=∠C
AD=AD
∴△ADB≌△ADC
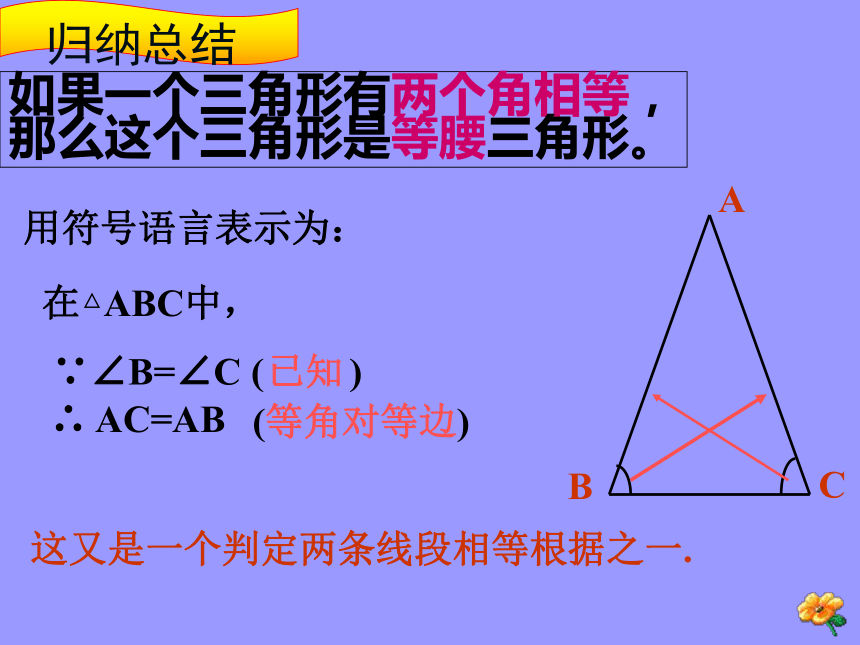
∴AB=AC12已知(等角对等边)如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。 在△ABC中, ∵∠B=∠C ( ) ∴ AC=AB 用符号语言表示为:这又是一个判定两条线段相等根据之一.
例:已知三角形一个外角的平分线平行于三角形 的一 边,请根据描述画出图形并写出几个你认为正确的结论。已知:∠CAE是△ABC 的外角, ∠1= ∠2, AD∥BC
结论: 第一层次:①∠1=∠B②∠2=∠C第二层次:③∠B=∠C第三层次:④AB=AC(两直线平行,同位角相等)(两直线平行,内错角相等)(等角对等边)清华探险队去野外考察,带了一根高为5m的标杆AB,如图,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,如果你是队长你知道需要多长的绳子吗?解:选取比例尺为1:100 (1cm代表1m)
<1> 作线段DE=4cm<2> 作线段DE的垂直平分线MN,与DE交于点B
<3> 在MN上截取BC=2.5cm<4> 连接CD,CE, ΔCDE就是所求等腰三角形<5> 量CD的长,计算出要求的绳长有两边相等的三角形是等腰三角形。2.等边对等角。3. 三线合一。4.是轴对称图形.2.等角对等边。1.有两边相等的三角形
是等腰三角形。1.两腰相等. 3.二线合一则等腰请把这个三角形纸片折成两个三角形,使其中一个三角形是等腰三角形!110°20°50°ACD2. 在△ABC中,已知AB=AC, BO平分∠ABC,CO平分
∠ACB ,过点O作直线EF//BC交AB于E ,交AC于F
<1>请问图中有多少个等腰三角形?说明理由
<2>线段EF和线段EB,FC之间有没有关系?若有,是什么关系?
<3>如果AB不等于AC,其它条件不变,这种关系还存在吗?FE0BCAEF 本软件:
设计:陈雪芬
制作:陈雪芬
感谢诸位老师的指导!
曾联合攻打魏国。如图所示,(蜀国沿BA行进,
吴国沿CA行进)当时测得∠B= ∠C,
如果蜀、吴军队以同样的速度同时出发,能不能大约同时赶
到魏国进行袭击?对于一个三角形,如果有两个角相等,那么它们所对的边有什么关系?一、问题情境BCA任画线段BC,分别以点B和点C为顶点,以BC为一边,在BC的同侧画两个相等的角,两角的终边相交A点.因此,在△ABC中,∠B=∠C.想一想如何比较AB与AC的数量关系?
已知:在△ABC中,∠B=∠C 求证:AB=AC (2)作∠A的平分线交BC于TABCT在△BAT和△CAT中
∵ ∠1=∠2(角平分线定义)
∠B=∠C(已知)
AT=AT(公共边)
∴△BAT≌△CAT(AAS)
∴AB=AC(全等三角形对应边相等)证明:(1)过A点作AD⊥BC,垂足为D.ABCD∵AD⊥BC
∴∠ADB=∠ADC= 90°
在△ADB和△ADC中
∵ ∠ADB=∠ADC
∠B=∠C
AD=AD
∴△ADB≌△ADC
∴AB=AC12已知(等角对等边)如果一个三角形有两个角相等,
那么这个三角形是等腰三角形。 在△ABC中, ∵∠B=∠C ( ) ∴ AC=AB 用符号语言表示为:这又是一个判定两条线段相等根据之一.
例:已知三角形一个外角的平分线平行于三角形 的一 边,请根据描述画出图形并写出几个你认为正确的结论。已知:∠CAE是△ABC 的外角, ∠1= ∠2, AD∥BC
结论: 第一层次:①∠1=∠B②∠2=∠C第二层次:③∠B=∠C第三层次:④AB=AC(两直线平行,同位角相等)(两直线平行,内错角相等)(等角对等边)清华探险队去野外考察,带了一根高为5m的标杆AB,如图,为了将它固定,需要由它的中点C向地面上与点B距离相等的D、E两点拉两条绳子,使得点D、B、E在一条直线上,量得DE=4m,如果你是队长你知道需要多长的绳子吗?解:选取比例尺为1:100 (1cm代表1m)
<1> 作线段DE=4cm<2> 作线段DE的垂直平分线MN,与DE交于点B
<3> 在MN上截取BC=2.5cm<4> 连接CD,CE, ΔCDE就是所求等腰三角形<5> 量CD的长,计算出要求的绳长有两边相等的三角形是等腰三角形。2.等边对等角。3. 三线合一。4.是轴对称图形.2.等角对等边。1.有两边相等的三角形
是等腰三角形。1.两腰相等. 3.二线合一则等腰请把这个三角形纸片折成两个三角形,使其中一个三角形是等腰三角形!110°20°50°ACD2. 在△ABC中,已知AB=AC, BO平分∠ABC,CO平分
∠ACB ,过点O作直线EF//BC交AB于E ,交AC于F
<1>请问图中有多少个等腰三角形?说明理由
<2>线段EF和线段EB,FC之间有没有关系?若有,是什么关系?
<3>如果AB不等于AC,其它条件不变,这种关系还存在吗?FE0BCAEF 本软件:
设计:陈雪芬
制作:陈雪芬
感谢诸位老师的指导!
