等腰三角形的性质
图片预览




文档简介
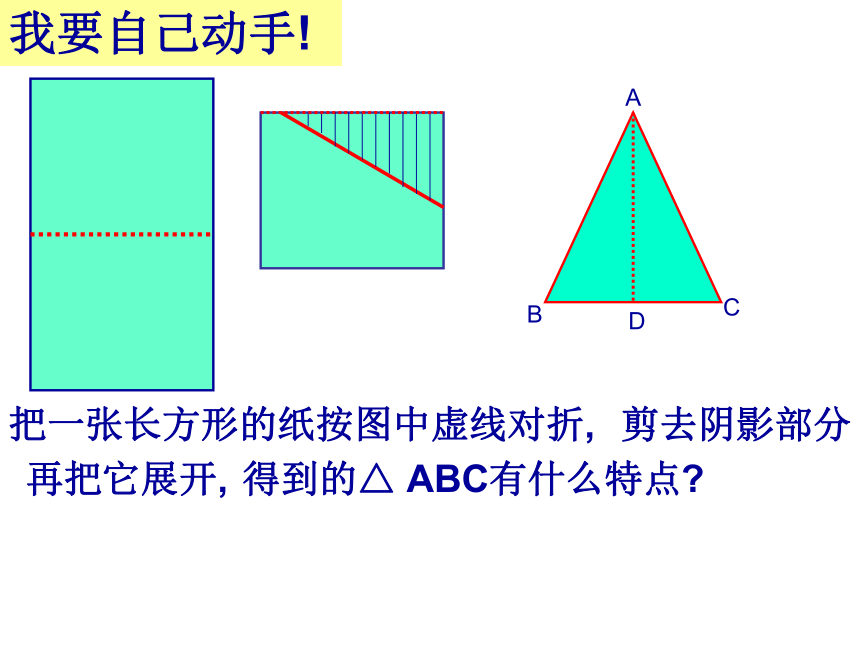
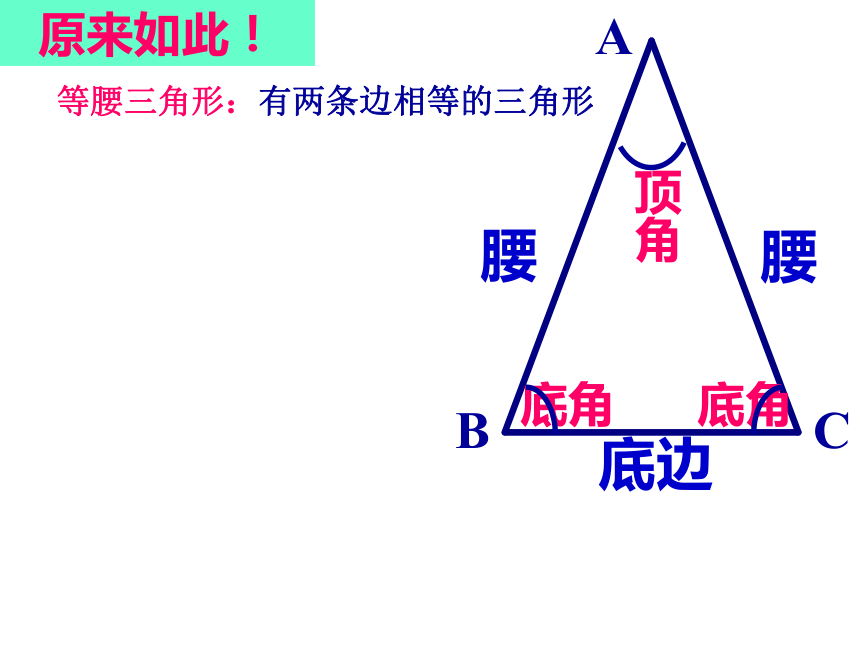
课件26张PPT。点线面体加减乘除描绘宏伟蓝图谋算千秋功业14.3.1等腰三角形我要自己动手!把一张长方形的纸按图中虚线对折,剪去阴影部分再把它展开,得到的△ ABC有什么特点?底边原来如此!等腰三角形:有两条边相等的三角形4、已知等腰三角形一边的长为3,另一边的长为5,
求它的周长。解:分两种情况:
(1)当腰长为3时,有3+3>5符合要求,
∴此时三角形的周长为3×2+5=11;
(2)当腰长为5时,有5+5>3符合要求,
∴此时三角形的周长为5×2+3=13.跟踪练习:
等腰三角形的两边长分别为2和7,那么它
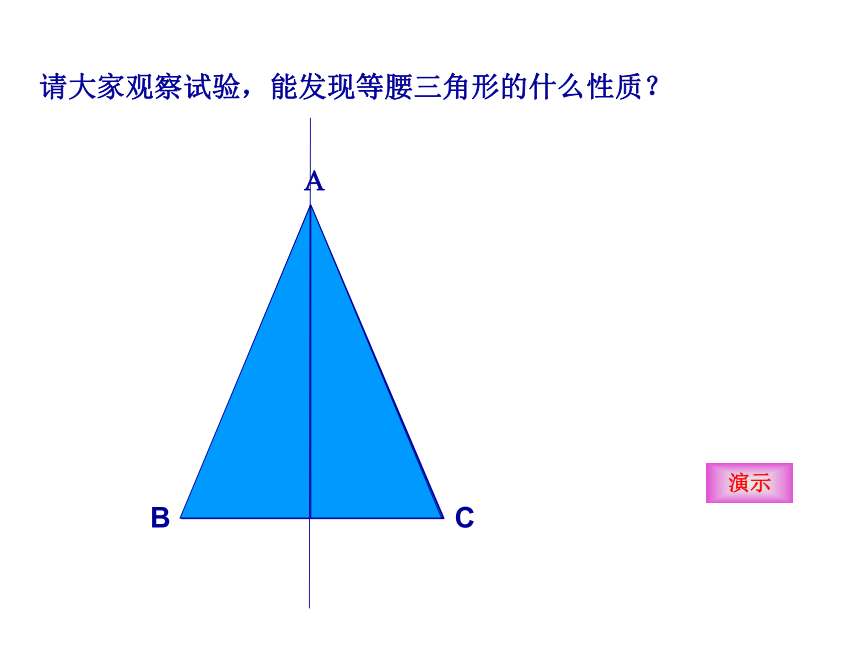
的周长是多少?请大家观察试验,能发现等腰三角形的什么性质?演示ABCD你知道吗?把剪出的等腰三角形ABC沿折痕对折,两旁的部分重合吗?这说明了什么?等腰三角形是轴对称图形.找出重合的线段和角。重合的角∠B∠C等腰三角形的两个底角相等(“等边对等角”)∠BAD∠CAD∠ADB∠ADC重合的线段BDCD等腰三角形的顶角平分线、底边上的高、底边上的中线相互重合。
(“三线合一”)等腰三角形的性质:顶角平分线所在的直线是它的对称轴.
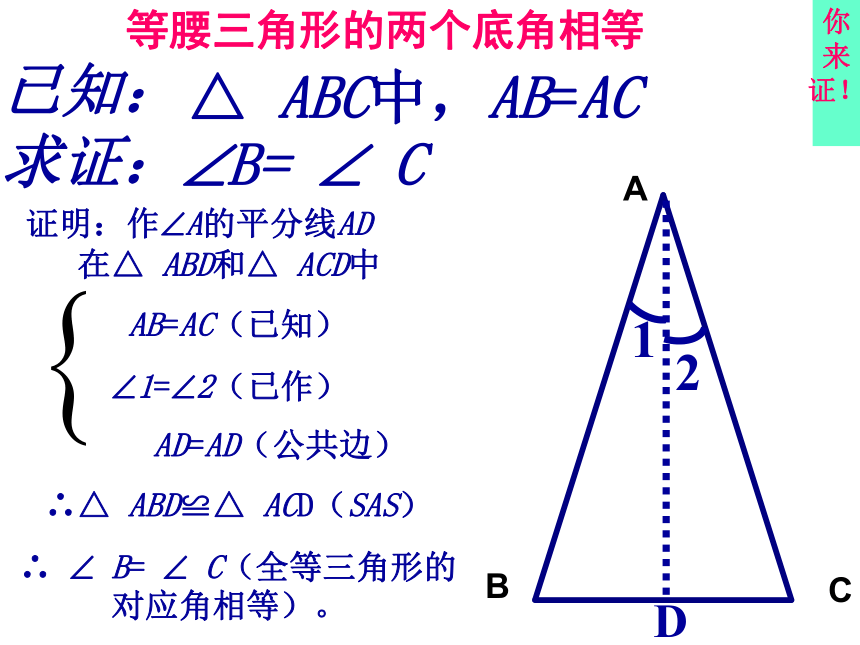
已知:
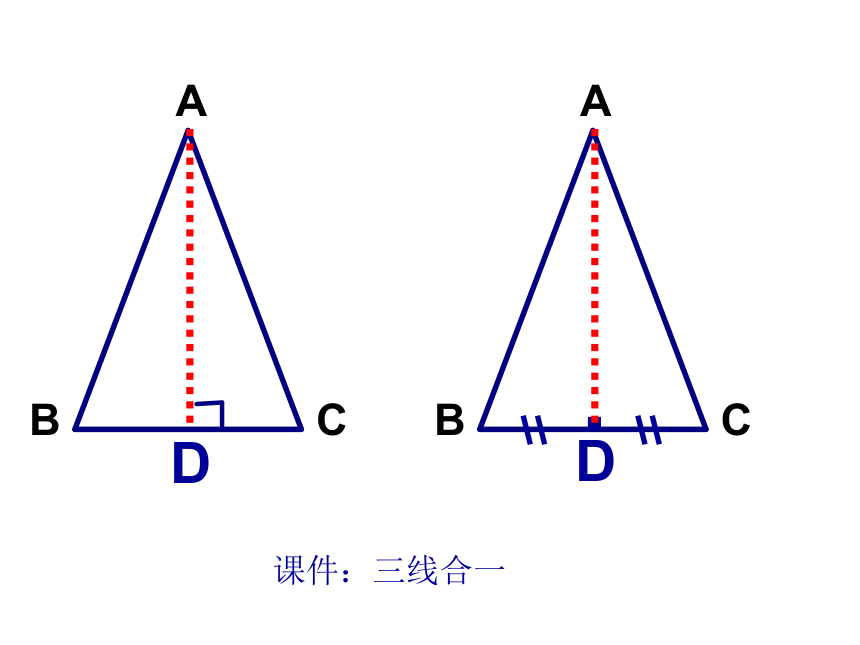
求证:证明:作?A的平分线AD 等腰三角形的两个底角相等?B= ? C△ ABC中,AB=AC你来证!课件:三线合一等腰三角形的性质定理等腰三角形的两个底角相等(简写成“等边对等角”) 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边. 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.“三线合一”在△ ABC中,AB=AC=BC,利用已有的知识,如何推导出
∠A、 ∠B 、∠C 的度数. 推论2 等边三角形的各角都相等,并且每一个角都
等于60 o .
判断下列语句是否正确。1.等腰三角形的角平分线、中线和高互相重合。( )
2.有一个角是60°的等腰三角形,其它两个内角也为60°. ( )
3.等腰三角形的底角都是锐角. ( )
4.钝角三角形不可能是等腰三角形 . ( )××作业巩固练习等腰三角形一个角为80°,它的另外两个角为
__________________.
解:分两种情况:
(1)当顶角为80°时,它的另外两个角为
__________________;
(2)当底角为80°时,它的另外两个角为
__________________.
50° , 50°80° , 20°⒈等腰三角形一个底角为70°,它的顶角为______.⒉等腰三角形一个角为70°,它的另外两个角为
__________________.⒊等腰三角形一个角为110°,它的另外两个角为_______.① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°
⑤0°<底角<90°结论:在等腰三角形中,40 °35 °,35 °70°,40°或55°,55° 4. 根据等腰三角形性质定理的推论,在△ABC中, AB=AC时, (1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD1、等腰三角形的一个底角等于75度,求它的顶角。2、等腰三角形的顶角等于50度,求它的底角。抢答!你一定行!3、如上图,求等腰三角形的底角的度数等腰三角形一个角为70°,求它的另外两个角。注意:锐角既可以作顶角,也可以作底角20分等腰三角形一个角为110°,求它的另外两个角。10分巩固练习1.填空题:
(1)如图,在△ ABC中,AB=AC,外角∠ ACD=100,则∠ B=____度
变式
(1)等腰三角形的一内角为100°,则它的顶角是_____
(2)等腰三角形的一外角为100°,则它的底角是_____ 已知:房屋顶角∠BAC=100。,过房顶A 的立柱AD⊥BC,房椽AB=AC,求顶架上∠B,∠C, ∠BAD,∠CAD的度数?20分例1 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
已知:如图, △ ABC中, ∠ABC=50 o,
∠ACB=80 o,延长CB至D,使BD=BA,
延长BC至E,使CE=CA .连结AD、AE.
求∠D、∠E、∠DAE的度数 .例:已知:在△ABC中,
AB=AC,点D在AC上,
且BD=BC=AD。①图中共有几个等腰三角形?②找出图中所有相等的角。三个: △ABC △ABD △BCD∠ABD= ∠BAD∠BDC= ∠C3= ∠ABC③∠3与∠A有什么关系?∠3=2 ∠A例:已知:在△ABC中,
AB=AC,点D在AC上,
且BD=BC=AD。求△ABC各角的度数1解:∵AB=AC ∴∠ABC=∠C= ∠1BD=BC=AD∠2= ∠A(等边对等角)设∠A=X,则∠1= ∠A+∠2=2X∴∠ABC=∠C= ∠1=2xxx2x2x2x在△ABC中:∠ABC+∠C+ ∠A=2x+2x+x=
180°∴x=36 °∴∠A=36 ° ∠ABC=∠C=72 °等腰三角形的性质定理等腰三角形的两个底角相等(简写成“等边对等角”) 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边. 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.“三线合一”本节课你的收获是什么?小结大家谈 本节课你学到了什么?
求它的周长。解:分两种情况:
(1)当腰长为3时,有3+3>5符合要求,
∴此时三角形的周长为3×2+5=11;
(2)当腰长为5时,有5+5>3符合要求,
∴此时三角形的周长为5×2+3=13.跟踪练习:
等腰三角形的两边长分别为2和7,那么它
的周长是多少?请大家观察试验,能发现等腰三角形的什么性质?演示ABCD你知道吗?把剪出的等腰三角形ABC沿折痕对折,两旁的部分重合吗?这说明了什么?等腰三角形是轴对称图形.找出重合的线段和角。重合的角∠B∠C等腰三角形的两个底角相等(“等边对等角”)∠BAD∠CAD∠ADB∠ADC重合的线段BDCD等腰三角形的顶角平分线、底边上的高、底边上的中线相互重合。
(“三线合一”)等腰三角形的性质:顶角平分线所在的直线是它的对称轴.
已知:
求证:证明:作?A的平分线AD 等腰三角形的两个底角相等?B= ? C△ ABC中,AB=AC你来证!课件:三线合一等腰三角形的性质定理等腰三角形的两个底角相等(简写成“等边对等角”) 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边. 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.“三线合一”在△ ABC中,AB=AC=BC,利用已有的知识,如何推导出
∠A、 ∠B 、∠C 的度数. 推论2 等边三角形的各角都相等,并且每一个角都
等于60 o .
判断下列语句是否正确。1.等腰三角形的角平分线、中线和高互相重合。( )
2.有一个角是60°的等腰三角形,其它两个内角也为60°. ( )
3.等腰三角形的底角都是锐角. ( )
4.钝角三角形不可能是等腰三角形 . ( )××作业巩固练习等腰三角形一个角为80°,它的另外两个角为
__________________.
解:分两种情况:
(1)当顶角为80°时,它的另外两个角为
__________________;
(2)当底角为80°时,它的另外两个角为
__________________.
50° , 50°80° , 20°⒈等腰三角形一个底角为70°,它的顶角为______.⒉等腰三角形一个角为70°,它的另外两个角为
__________________.⒊等腰三角形一个角为110°,它的另外两个角为_______.① 顶角+2×底角=180°② 顶角=180°-2×底角③ 底角=(180°-顶角)÷2④0°<顶角<180°
⑤0°<底角<90°结论:在等腰三角形中,40 °35 °,35 °70°,40°或55°,55° 4. 根据等腰三角形性质定理的推论,在△ABC中, AB=AC时, (1) ∵AD⊥BC,∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD1、等腰三角形的一个底角等于75度,求它的顶角。2、等腰三角形的顶角等于50度,求它的底角。抢答!你一定行!3、如上图,求等腰三角形的底角的度数等腰三角形一个角为70°,求它的另外两个角。注意:锐角既可以作顶角,也可以作底角20分等腰三角形一个角为110°,求它的另外两个角。10分巩固练习1.填空题:
(1)如图,在△ ABC中,AB=AC,外角∠ ACD=100,则∠ B=____度
变式
(1)等腰三角形的一内角为100°,则它的顶角是_____
(2)等腰三角形的一外角为100°,则它的底角是_____ 已知:房屋顶角∠BAC=100。,过房顶A 的立柱AD⊥BC,房椽AB=AC,求顶架上∠B,∠C, ∠BAD,∠CAD的度数?20分例1 已知:如图,房屋的顶角∠BAC=100 o, 过屋顶A的立柱AD ? BC , 屋椽AB=AC. 求顶架上∠B、∠C、∠BAD、
∠CAD的度数.
已知:如图, △ ABC中, ∠ABC=50 o,
∠ACB=80 o,延长CB至D,使BD=BA,
延长BC至E,使CE=CA .连结AD、AE.
求∠D、∠E、∠DAE的度数 .例:已知:在△ABC中,
AB=AC,点D在AC上,
且BD=BC=AD。①图中共有几个等腰三角形?②找出图中所有相等的角。三个: △ABC △ABD △BCD∠ABD= ∠BAD∠BDC= ∠C3= ∠ABC③∠3与∠A有什么关系?∠3=2 ∠A例:已知:在△ABC中,
AB=AC,点D在AC上,
且BD=BC=AD。求△ABC各角的度数1解:∵AB=AC ∴∠ABC=∠C= ∠1BD=BC=AD∠2= ∠A(等边对等角)设∠A=X,则∠1= ∠A+∠2=2X∴∠ABC=∠C= ∠1=2xxx2x2x2x在△ABC中:∠ABC+∠C+ ∠A=2x+2x+x=
180°∴x=36 °∴∠A=36 ° ∠ABC=∠C=72 °等腰三角形的性质定理等腰三角形的两个底角相等(简写成“等边对等角”) 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边. 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.“三线合一”本节课你的收获是什么?小结大家谈 本节课你学到了什么?
