12.1平方差公式课件
图片预览





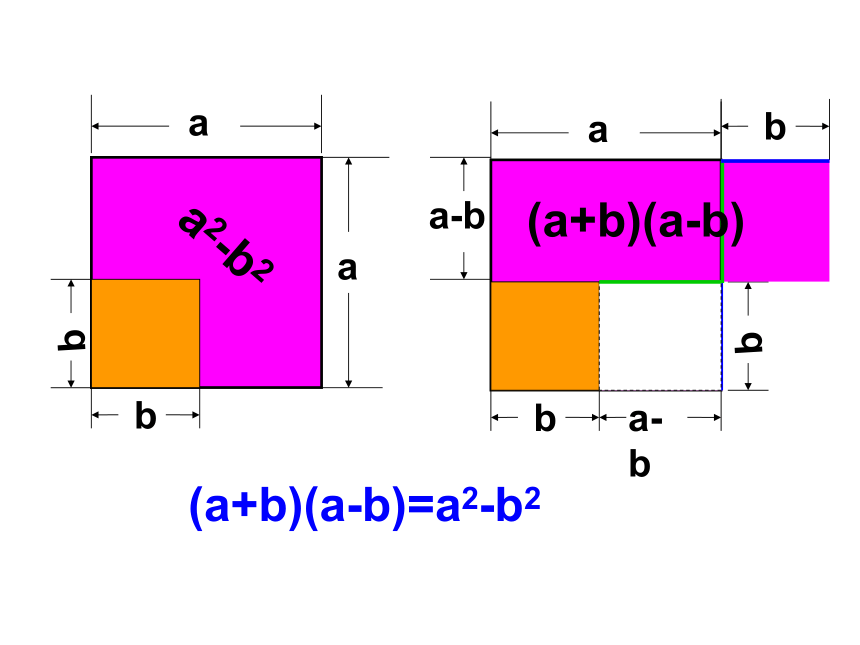


文档简介
课件23张PPT。12.1平方差公式
1、会推导平方差公式:(a+b)(a-b)=a2-b2,
了解公式的几何解释,并能运用公式进行计算。
2、经历探索平方差公式的过程,发展符号意识,体会特殊→一般→特殊的认识规律和数形结合思想。
3、通过自主探究,合作交流活动,体验合作学习的快乐。
【学习重点和难点】
1、学习重点:平方差公式的推导和应用
2、学习难点:平方差公式的几何拼图验证及灵 活运用平方差公式学习目标 你能回答多项式的乘法法则吗?① (x + 2)( x-2)
②(1 + 3a)( 1-3a)
③(m+ 5n)( m-5n)
④(3y + z)(3y-z)算一算,比一比,看谁算得又快又准 =x2 - 4=1 -9a2=m2 - 25n2= 9y2 - z2=x2 - 22=12-(3a)2=m2 - (5n)2=(3y)2 - z2(a+b)(a-b)=a2-b2你能证明(a+b)(a-b)=a2-b2吗?1、利用多项式的乘法法则验证: (a+b)(a-b)2、利用图形的面积证明。 =a2-ab+ab-b2
= a2-b2
a2-b2(a+b)(a-b)=a2-b2(a+b)(a-b)平方差公式:(a+b)(a?b)=a2?b2 两数和与这两数差的积,等于这两数的平方差.
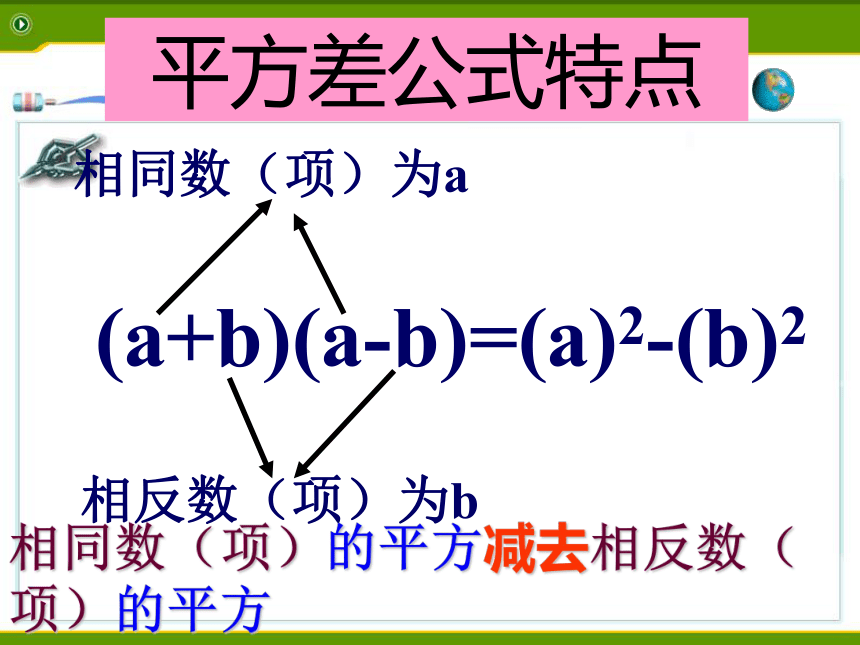
(a+b)(a-b)=(a)2-(b)2相反数(项)为b 相同数(项)为a 平方差公式特点相同数(项)的平方减去相反数(项)的平方★结构特点数学表达式1.左边是两个二项式相乘,并且有一项完全相同;另一项互为相反数2.右边是乘式中两项的平方差,即(相同项)2 -(相反项)2a、b可以表示数,还可以表示单项式或多项式。概念挖掘★字母a、b的代表性:
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
?(4)(a-b)(-a-b)= _________a2-b2a2-b2b2-a2b2-a2相同项的平方减去相反项的平方1、参照平方差公式“(a+b)(a-b)=a2-b2”填空。(1+x)(1-x)(-3+a)(-3-a)(0.3x-1)(1+0.3x)(1+a)(-1+a)aba2-b21x-3a12-x2(-3)2-a2a1a2-12 0.3x1( 0.3x)2-12(a-b)(a+b)2、利用平方差公式填表。3、判断下列式子是否可用平方差公式。 (1)(-a+b)(a+b)
(2) (-2a+b)(-2a-b)
(3) (-a+b)(a-b)
(4) (a+b)(a-c)(是) (是)(否)(否)解:(1) (3x+2y )( 3x-2y)
=(3x)2-(2y)2
=9x2-4y2 (2) (-7+2m2)(-7-2m2)
=(-7)2-(2m2)2
=49-4m4
(3) (X-1)(X+1)(X2+1)
=(X2-1)(X2+1)
=x4-1
例2、计算:
1、102 ×98
2、 ( y+2)( y-2 ) - ( y-1 )( y+5)解:1、原式= ( 100+2)( 100-2 ) =10000-4= 1002 - 22
=9996例2、计算:
1、102 ×98解:2、原式=y2 – 22 - ( y2 +5y-y-5)= y2 – 4 – (y2 +4y-5)
= y2 – 4 – y2 -4y+5
=-4y+1
注:合并同类项,化到最简。
2、随堂练习1、2、3、4、(1) (1+3x)(1?3x)=1?3x2
(2) (3a2+b2)(3a2?b2)=3a4?b4
(3) (3x+2y)(3x?2y)=3x2?2y2指出下列计算中的错误: 第二数被平方时,未添括号。第一数被平方时,未添括号。第一数与第二数被平方时,都未添括号。火眼金睛1、 利用平方差公式计算: 挑战自我拓展应用1、什么是平方差公式?2、运用公式要注意:(1)要符合公式特征才能运用平方差公式;(2)有些式子表面不能应用公式,但实质能应用公式,要注意变形。小结:通过本节课的学习你有什么收获?1、小莹同学在计算 时,
将积式乘以(2-1)得:
解:原式=
=?
=
=
你能根据上题计算:
(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)(264+1)
拓展延伸,挑战自己!
1、 课本112页习题12.1第1题
课后作业谢谢大家
1、会推导平方差公式:(a+b)(a-b)=a2-b2,
了解公式的几何解释,并能运用公式进行计算。
2、经历探索平方差公式的过程,发展符号意识,体会特殊→一般→特殊的认识规律和数形结合思想。
3、通过自主探究,合作交流活动,体验合作学习的快乐。
【学习重点和难点】
1、学习重点:平方差公式的推导和应用
2、学习难点:平方差公式的几何拼图验证及灵 活运用平方差公式学习目标 你能回答多项式的乘法法则吗?① (x + 2)( x-2)
②(1 + 3a)( 1-3a)
③(m+ 5n)( m-5n)
④(3y + z)(3y-z)算一算,比一比,看谁算得又快又准 =x2 - 4=1 -9a2=m2 - 25n2= 9y2 - z2=x2 - 22=12-(3a)2=m2 - (5n)2=(3y)2 - z2(a+b)(a-b)=a2-b2你能证明(a+b)(a-b)=a2-b2吗?1、利用多项式的乘法法则验证: (a+b)(a-b)2、利用图形的面积证明。 =a2-ab+ab-b2
= a2-b2
a2-b2(a+b)(a-b)=a2-b2(a+b)(a-b)平方差公式:(a+b)(a?b)=a2?b2 两数和与这两数差的积,等于这两数的平方差.
(a+b)(a-b)=(a)2-(b)2相反数(项)为b 相同数(项)为a 平方差公式特点相同数(项)的平方减去相反数(项)的平方★结构特点数学表达式1.左边是两个二项式相乘,并且有一项完全相同;另一项互为相反数2.右边是乘式中两项的平方差,即(相同项)2 -(相反项)2a、b可以表示数,还可以表示单项式或多项式。概念挖掘★字母a、b的代表性:
(l)(-a+b)(a+b)=??_________
(2)(a-b)(b+a)= __________
(3)(-a-b)(-a+b)= ________
?(4)(a-b)(-a-b)= _________a2-b2a2-b2b2-a2b2-a2相同项的平方减去相反项的平方1、参照平方差公式“(a+b)(a-b)=a2-b2”填空。(1+x)(1-x)(-3+a)(-3-a)(0.3x-1)(1+0.3x)(1+a)(-1+a)aba2-b21x-3a12-x2(-3)2-a2a1a2-12 0.3x1( 0.3x)2-12(a-b)(a+b)2、利用平方差公式填表。3、判断下列式子是否可用平方差公式。 (1)(-a+b)(a+b)
(2) (-2a+b)(-2a-b)
(3) (-a+b)(a-b)
(4) (a+b)(a-c)(是) (是)(否)(否)解:(1) (3x+2y )( 3x-2y)
=(3x)2-(2y)2
=9x2-4y2 (2) (-7+2m2)(-7-2m2)
=(-7)2-(2m2)2
=49-4m4
(3) (X-1)(X+1)(X2+1)
=(X2-1)(X2+1)
=x4-1
例2、计算:
1、102 ×98
2、 ( y+2)( y-2 ) - ( y-1 )( y+5)解:1、原式= ( 100+2)( 100-2 ) =10000-4= 1002 - 22
=9996例2、计算:
1、102 ×98解:2、原式=y2 – 22 - ( y2 +5y-y-5)= y2 – 4 – (y2 +4y-5)
= y2 – 4 – y2 -4y+5
=-4y+1
注:合并同类项,化到最简。
2、随堂练习1、2、3、4、(1) (1+3x)(1?3x)=1?3x2
(2) (3a2+b2)(3a2?b2)=3a4?b4
(3) (3x+2y)(3x?2y)=3x2?2y2指出下列计算中的错误: 第二数被平方时,未添括号。第一数被平方时,未添括号。第一数与第二数被平方时,都未添括号。火眼金睛1、 利用平方差公式计算: 挑战自我拓展应用1、什么是平方差公式?2、运用公式要注意:(1)要符合公式特征才能运用平方差公式;(2)有些式子表面不能应用公式,但实质能应用公式,要注意变形。小结:通过本节课的学习你有什么收获?1、小莹同学在计算 时,
将积式乘以(2-1)得:
解:原式=
=?
=
=
你能根据上题计算:
(2+1)(22+1)(24+1)(28+1)(216+1)(232+1)(264+1)
拓展延伸,挑战自己!
1、 课本112页习题12.1第1题
课后作业谢谢大家
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
