2.1 整式 第2课时 课件(共15张PPT)2023-2024学年人教版七年级数学上册
文档属性
| 名称 | 2.1 整式 第2课时 课件(共15张PPT)2023-2024学年人教版七年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
2.1 整式
第2课时
第二章 整式的加减
1.理解单项式、单项式的系数和次数的概念;
2.能准确找出单项式的系数和次数.
活动1:用含有字母的式子填空.
(1)边长为m的正方形的周长为 ,面积为 ;
(2)铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价是 元;
(3)一辆汽车的速度是v km/h,t小时的行驶路程为 km;
(4)半径为r cm的圆的周长是 cm,面积为 cm2;
(5)一个长方形的长是2.5m,宽是x m,这个长方形的面积是 m2.
任务一:理解单项式有关概念
4m
m2
2.5x
πr2
2πr
vt
2.5x
同一个式子可以表示不同含义.
问题1:上述所填的式子有什么特点?
4m m2 2.5x πr πr2
问题2:观察下列式子有什么不同?
4r2 r2 -r2 πr2
问题3:观察下列式子有什么不同?
2ab 2ab2 2a2b2
数与字母、字母与字母的运算都是乘法运算.
数字因数不同
字母指数的和不同
π是常数,表示圆周率.
如果一个式子是由数或字母的积组成,那么这个式子叫做单项式.
单项式:2a2b2
单项式中的数字因数叫做单项式系数.
2+2=4
单项式中的所有字母指数的和叫做单项式的次数.
叫做四次单项式
如果一个式子是由数或字母的积组成,那么这个式子叫做单项式.
活动2:火眼金睛——快速认出下列式子中的单项式.
3x-y,0,0.72a,x2y, ,π, , ,m
√
√
√
√
√
√
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法
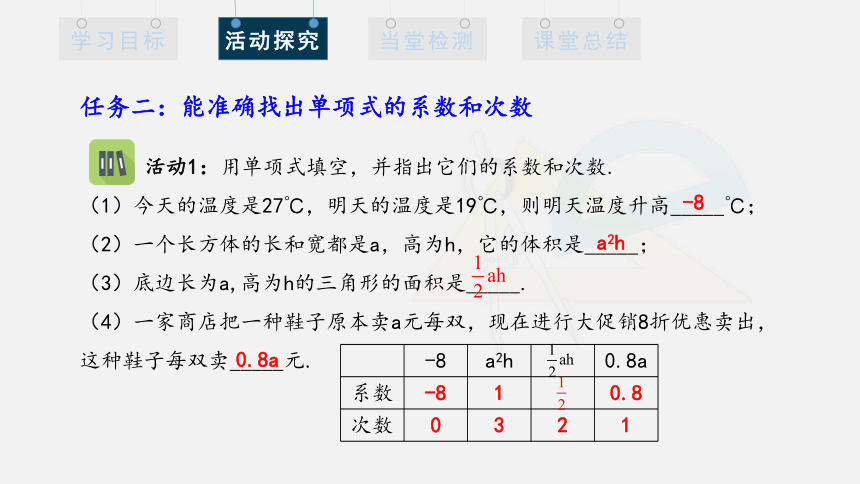
活动1:用单项式填空,并指出它们的系数和次数.
(1)今天的温度是27℃,明天的温度是19℃,则明天温度升高_____℃;
(2)一个长方体的长和宽都是a,高为h,它的体积是_____;
(3)底边长为a,高为h的三角形的面积是_____.
(4)一家商店把一种鞋子原本卖a元每双,现在进行大促销8折优惠卖出,这种鞋子每双卖_____元.
任务二:能准确找出单项式的系数和次数
-8
a2h
0.8a
-8 a2h 0.8a
系数 -8 1 0.8
次数 0 3 2 1
游戏大比拼
游戏规则:
1.组内竞争:在各组内每名学生都写出三个单项式,让组内其他学生抢答单项式的系数和次数,选出回答最优秀的学生.
2.组间竞争:各组选出一个优秀代表,把自己组举出的认为最好的三个单项式展示给大家,其他各组学生抢答,并做出评判.看哪组学生答对的最多,选出最优秀的组.
确定单项式的系数和次数时应注意:
1.圆周率π是常数;
2.当一个单项式的系数是1或-1时,“1”通常省略不写;
3.单项式的系数应包括它前面的性质符号;
4.省略1的字母指数别漏掉;
5.单项式次数只与字母的指数有关,单独一个非零的数,其次数为0.
活动小结
活动2:根据单项式的相关概念,解决问题.
(1)写出系数为–3,含有字母x、y且次数为5的单项式.
(2)若(a+3)xby2是关于x,y的五次单项式,求a,b应满足的条件.
解:(1)-3xy4,-3x2y3,-3x3y2,-3x4y;
(2)(a+3)xby2是关于x,y的五次单项式,
所以a+3≠0,b+2=5,
所以a≠-3,b=3.
练一练
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1;( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 .( )
×
×
×
×
×
√
判断下列说法是否正确:
1.下列赋予“4m”实际意义的叙述中不正确的是( )
A.若葡萄的价格是4元/千克,则4m表示买 m千克葡萄的金额
B.若m表示一个正方形的边长,则4m表示这个正方形的周长
C.若三角形的底边长为3,面积为6m,则4m表示此边上的高
D.若4和m分别表示一个两位数中的十位数字和个位数字,则4m表示这个两位数
D
2.下列各式中,是四次单项式的为( )
A.4xy B.x4y
C.-x2yz D.x4+y4
3.单项式-3xy2z3的系数与次数的和为( )
A.6 B.3
C.-3 D.-6
C
B
4.下列各组单项式中,次数相同的是( )
A.3ab与-4xy2 B.3π与a
C.-2x2y2与xy D.a3与xy2
5.若ax2yb-1是关于x,y的单项式,系数为6,次数是3,
则a= ,b= .
2
6
D
1.怎样判断一个式子是不是单项式?
2.确定单项式的系数和次数时需要注意哪些?
2.1 整式
第2课时
第二章 整式的加减
1.理解单项式、单项式的系数和次数的概念;
2.能准确找出单项式的系数和次数.
活动1:用含有字母的式子填空.
(1)边长为m的正方形的周长为 ,面积为 ;
(2)铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价是 元;
(3)一辆汽车的速度是v km/h,t小时的行驶路程为 km;
(4)半径为r cm的圆的周长是 cm,面积为 cm2;
(5)一个长方形的长是2.5m,宽是x m,这个长方形的面积是 m2.
任务一:理解单项式有关概念
4m
m2
2.5x
πr2
2πr
vt
2.5x
同一个式子可以表示不同含义.
问题1:上述所填的式子有什么特点?
4m m2 2.5x πr πr2
问题2:观察下列式子有什么不同?
4r2 r2 -r2 πr2
问题3:观察下列式子有什么不同?
2ab 2ab2 2a2b2
数与字母、字母与字母的运算都是乘法运算.
数字因数不同
字母指数的和不同
π是常数,表示圆周率.
如果一个式子是由数或字母的积组成,那么这个式子叫做单项式.
单项式:2a2b2
单项式中的数字因数叫做单项式系数.
2+2=4
单项式中的所有字母指数的和叫做单项式的次数.
叫做四次单项式
如果一个式子是由数或字母的积组成,那么这个式子叫做单项式.
活动2:火眼金睛——快速认出下列式子中的单项式.
3x-y,0,0.72a,x2y, ,π, , ,m
√
√
√
√
√
√
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法
活动1:用单项式填空,并指出它们的系数和次数.
(1)今天的温度是27℃,明天的温度是19℃,则明天温度升高_____℃;
(2)一个长方体的长和宽都是a,高为h,它的体积是_____;
(3)底边长为a,高为h的三角形的面积是_____.
(4)一家商店把一种鞋子原本卖a元每双,现在进行大促销8折优惠卖出,这种鞋子每双卖_____元.
任务二:能准确找出单项式的系数和次数
-8
a2h
0.8a
-8 a2h 0.8a
系数 -8 1 0.8
次数 0 3 2 1
游戏大比拼
游戏规则:
1.组内竞争:在各组内每名学生都写出三个单项式,让组内其他学生抢答单项式的系数和次数,选出回答最优秀的学生.
2.组间竞争:各组选出一个优秀代表,把自己组举出的认为最好的三个单项式展示给大家,其他各组学生抢答,并做出评判.看哪组学生答对的最多,选出最优秀的组.
确定单项式的系数和次数时应注意:
1.圆周率π是常数;
2.当一个单项式的系数是1或-1时,“1”通常省略不写;
3.单项式的系数应包括它前面的性质符号;
4.省略1的字母指数别漏掉;
5.单项式次数只与字母的指数有关,单独一个非零的数,其次数为0.
活动小结
活动2:根据单项式的相关概念,解决问题.
(1)写出系数为–3,含有字母x、y且次数为5的单项式.
(2)若(a+3)xby2是关于x,y的五次单项式,求a,b应满足的条件.
解:(1)-3xy4,-3x2y3,-3x3y2,-3x4y;
(2)(a+3)xby2是关于x,y的五次单项式,
所以a+3≠0,b+2=5,
所以a≠-3,b=3.
练一练
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1;( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 .( )
×
×
×
×
×
√
判断下列说法是否正确:
1.下列赋予“4m”实际意义的叙述中不正确的是( )
A.若葡萄的价格是4元/千克,则4m表示买 m千克葡萄的金额
B.若m表示一个正方形的边长,则4m表示这个正方形的周长
C.若三角形的底边长为3,面积为6m,则4m表示此边上的高
D.若4和m分别表示一个两位数中的十位数字和个位数字,则4m表示这个两位数
D
2.下列各式中,是四次单项式的为( )
A.4xy B.x4y
C.-x2yz D.x4+y4
3.单项式-3xy2z3的系数与次数的和为( )
A.6 B.3
C.-3 D.-6
C
B
4.下列各组单项式中,次数相同的是( )
A.3ab与-4xy2 B.3π与a
C.-2x2y2与xy D.a3与xy2
5.若ax2yb-1是关于x,y的单项式,系数为6,次数是3,
则a= ,b= .
2
6
D
1.怎样判断一个式子是不是单项式?
2.确定单项式的系数和次数时需要注意哪些?
