2.1 整式 第3课时 课件(共15张PPT) 2023-—2024学年人教版数学七年级上册
文档属性
| 名称 | 2.1 整式 第3课时 课件(共15张PPT) 2023-—2024学年人教版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 08:56:26 | ||
图片预览





文档简介
(共15张PPT)
2.1 整式
第3课时
第二章 整式的加减
1.理解多项式、整式的概念;
2.能准确找出多项式的系数和次数;
3.能列多项式解决问题.
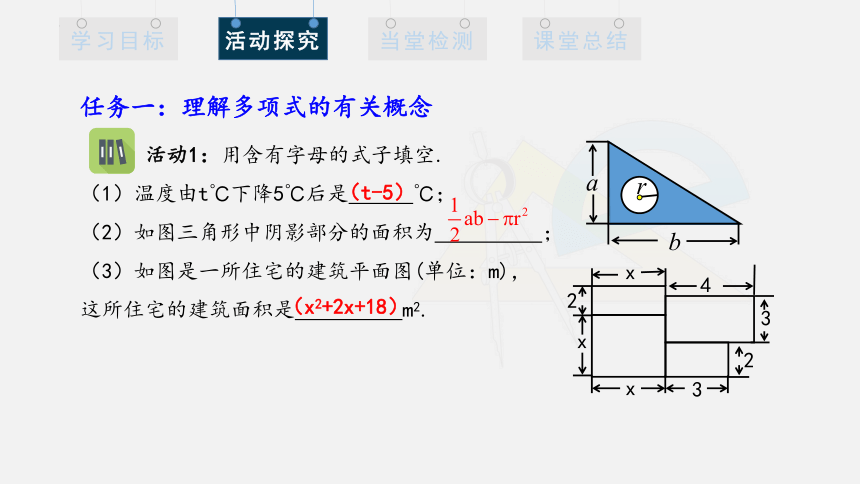
活动1:用含有字母的式子填空.
(1)温度由t℃下降5℃后是 ℃;
(2)如图三角形中阴影部分的面积为 ;
(3)如图是一所住宅的建筑平面图(单位:m),
这所住宅的建筑面积是 m2.
任务一:理解多项式的有关概念
a
b
r
x
x
x
2
4
3
2
3
(t-5)
(x2+2x+18)
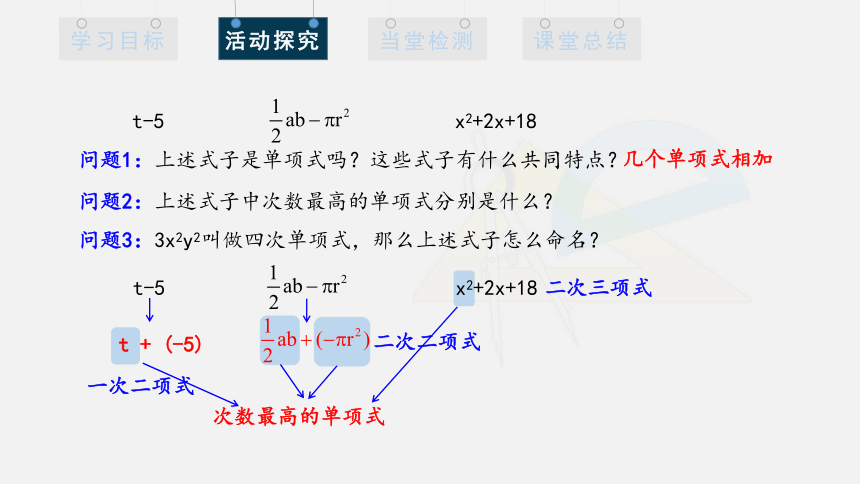
t-5 x2+2x+18
问题1:上述式子是单项式吗?这些式子有什么共同特点?
问题2:上述式子中次数最高的单项式分别是什么?
问题3:3x2y2叫做四次单项式,那么上述式子怎么命名?
t-5 x2+2x+18
次数最高的单项式
t + (-5)
二次三项式
二次二项式
一次二项式
几个单项式相加
多项式最高次项可以不唯一.
1.几个单项式的和叫做多项式.其中每个单项式的叫做多项式的项,不含字母的项叫做常数项.次数最高项的次数,叫做这个多项式的次数.
2.单项式与多项式统称整式.
新知生成
活动2:火眼金睛——指出下列式子中的单项式、多项式、整式.
x-5, , , , , ,-6, .
解:单项式:
多项式:
整式:
练一练
对于式子: , , ,3x2+5x-2,abc,0, ,m,下列说法正确的是( )
A.有5个单项式,1个多项式 B.有3个单项式,2个多项式
C.有4个单项式,2个多项式 D.有7个整式
C
活动1:指出下列多项式的项和次数,并说明多项式是几次几项式.
(1)x3-2xy3+x2y4-3y3-1;(2)7-x3-5xy;(3)3x2-x2y2+2x3y-1.
任务二:能准确找出多项式的项和次数
解:(1)项:x3、-2xy3、x2y4、-3y3、-1,
因为次数最高项为x2y4,次数为6,
所以是六次五项式;
(2)项:7、-x3、-5xy,
因为次数最高项为-x3,次数为3,
所以是三次三项式;
(3)项:3x2、-x2y2、2x3y、-1,
因为次数最高项为-x2y2,2x3y,次数为4,所以是四次四项式.
几次几项式的数字要大写.
确定多项式的项和次数时应注意:
1.多项式的各项应包括它前面的符号;
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的项的次数;
4.一个多项式的最高次项可以不唯一.
活动小结
活动2:根据多项式的相关概念,解决问题.
已知:多项式:3x2ym+(n-2)xy+16.
(1)如果多项式的次数为4次,则m为多少?
(2)如果多项式是二项式,则n为多少?
解:这个多项式的项有:3x2ym、(n-2)xy、16,
所以次数最高的项为3x2ym,次数为m+2.
(1)因为这个多项式的次数为4,所以m+2=4,所以m=2;
(2)因为这个多项式是二项式,即(n-2)xy不存在,
所以n-2=0,所以n=2.
变式:已知多项式-xym+1+x3y-2x3+3是六次四项式,单项式2a7-mbn与该多项式次数相同,求m、n的值.
解:因为多项式-xym+1+x3y-2x3+3是六次四项式,-xym+1的次数是1+m+1,x3y的次数是4,-2x3的次数是3,
所以1+m+1=6,所以m=4,
因为单项式2a7-mbn与该多项式次数相同,所以7-m+n=6,
所以7-4+n=6,所以n=3,
故m=4,n=3.
活动:如图所示, 用式子表示圆环的面积. 当R=15cm,r=10cm时,求圆环的面积(π取3.14).
任务三:列多项式解决问题
解:外圆的面积减去内圆的面积就是圆环的面积,
所以圆环的面积是πR2-πr2 .
当R=15 cm,r=10 cm时,圆环的面积(单位:cm2)是:πR2-πr2=3.14×152-3.14×102 =392.5,
答:这个圆环的面积是392.5cm2.
1.下列说法错误的是( )
A.m是单项式也是整式 B.整式一定是单项式
C. m-n是多项式也是整式 D.整式不一定是多项式
2.关于多项式6x2-3x2y3-4y3-10,下列说法正确的是( )
A.它是五次三项式 B.它的最高次项的系数为-4
C.它的常数项为10 D.它的二次项系数为6
3.如果xn-2-5x+2是关于x的三次三项式,那么n等于( )
A.3 B.4 C.5 D.6
B
D
C
4.填空.
(1)a,b分别表示长方形的长和宽,则长方形的周长l= ,面积s= ,当a=2cm,b=3cm时,l= cm, s= cm2.
(2)a,b分别表示梯形的上底和下底,h表示梯形的高,则梯形面积s= ,当a=2cm,b=4cm,h=5cm时,s= cm2.
2(a+b)
ab
10
6
15
回顾本节课,说一说你都学到了哪些知识?
整式
单项式
多项式
多项式的次数
常数项
概念
项
2.1 整式
第3课时
第二章 整式的加减
1.理解多项式、整式的概念;
2.能准确找出多项式的系数和次数;
3.能列多项式解决问题.
活动1:用含有字母的式子填空.
(1)温度由t℃下降5℃后是 ℃;
(2)如图三角形中阴影部分的面积为 ;
(3)如图是一所住宅的建筑平面图(单位:m),
这所住宅的建筑面积是 m2.
任务一:理解多项式的有关概念
a
b
r
x
x
x
2
4
3
2
3
(t-5)
(x2+2x+18)
t-5 x2+2x+18
问题1:上述式子是单项式吗?这些式子有什么共同特点?
问题2:上述式子中次数最高的单项式分别是什么?
问题3:3x2y2叫做四次单项式,那么上述式子怎么命名?
t-5 x2+2x+18
次数最高的单项式
t + (-5)
二次三项式
二次二项式
一次二项式
几个单项式相加
多项式最高次项可以不唯一.
1.几个单项式的和叫做多项式.其中每个单项式的叫做多项式的项,不含字母的项叫做常数项.次数最高项的次数,叫做这个多项式的次数.
2.单项式与多项式统称整式.
新知生成
活动2:火眼金睛——指出下列式子中的单项式、多项式、整式.
x-5, , , , , ,-6, .
解:单项式:
多项式:
整式:
练一练
对于式子: , , ,3x2+5x-2,abc,0, ,m,下列说法正确的是( )
A.有5个单项式,1个多项式 B.有3个单项式,2个多项式
C.有4个单项式,2个多项式 D.有7个整式
C
活动1:指出下列多项式的项和次数,并说明多项式是几次几项式.
(1)x3-2xy3+x2y4-3y3-1;(2)7-x3-5xy;(3)3x2-x2y2+2x3y-1.
任务二:能准确找出多项式的项和次数
解:(1)项:x3、-2xy3、x2y4、-3y3、-1,
因为次数最高项为x2y4,次数为6,
所以是六次五项式;
(2)项:7、-x3、-5xy,
因为次数最高项为-x3,次数为3,
所以是三次三项式;
(3)项:3x2、-x2y2、2x3y、-1,
因为次数最高项为-x2y2,2x3y,次数为4,所以是四次四项式.
几次几项式的数字要大写.
确定多项式的项和次数时应注意:
1.多项式的各项应包括它前面的符号;
2.多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号;
3.要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的项的次数;
4.一个多项式的最高次项可以不唯一.
活动小结
活动2:根据多项式的相关概念,解决问题.
已知:多项式:3x2ym+(n-2)xy+16.
(1)如果多项式的次数为4次,则m为多少?
(2)如果多项式是二项式,则n为多少?
解:这个多项式的项有:3x2ym、(n-2)xy、16,
所以次数最高的项为3x2ym,次数为m+2.
(1)因为这个多项式的次数为4,所以m+2=4,所以m=2;
(2)因为这个多项式是二项式,即(n-2)xy不存在,
所以n-2=0,所以n=2.
变式:已知多项式-xym+1+x3y-2x3+3是六次四项式,单项式2a7-mbn与该多项式次数相同,求m、n的值.
解:因为多项式-xym+1+x3y-2x3+3是六次四项式,-xym+1的次数是1+m+1,x3y的次数是4,-2x3的次数是3,
所以1+m+1=6,所以m=4,
因为单项式2a7-mbn与该多项式次数相同,所以7-m+n=6,
所以7-4+n=6,所以n=3,
故m=4,n=3.
活动:如图所示, 用式子表示圆环的面积. 当R=15cm,r=10cm时,求圆环的面积(π取3.14).
任务三:列多项式解决问题
解:外圆的面积减去内圆的面积就是圆环的面积,
所以圆环的面积是πR2-πr2 .
当R=15 cm,r=10 cm时,圆环的面积(单位:cm2)是:πR2-πr2=3.14×152-3.14×102 =392.5,
答:这个圆环的面积是392.5cm2.
1.下列说法错误的是( )
A.m是单项式也是整式 B.整式一定是单项式
C. m-n是多项式也是整式 D.整式不一定是多项式
2.关于多项式6x2-3x2y3-4y3-10,下列说法正确的是( )
A.它是五次三项式 B.它的最高次项的系数为-4
C.它的常数项为10 D.它的二次项系数为6
3.如果xn-2-5x+2是关于x的三次三项式,那么n等于( )
A.3 B.4 C.5 D.6
B
D
C
4.填空.
(1)a,b分别表示长方形的长和宽,则长方形的周长l= ,面积s= ,当a=2cm,b=3cm时,l= cm, s= cm2.
(2)a,b分别表示梯形的上底和下底,h表示梯形的高,则梯形面积s= ,当a=2cm,b=4cm,h=5cm时,s= cm2.
2(a+b)
ab
10
6
15
回顾本节课,说一说你都学到了哪些知识?
整式
单项式
多项式
多项式的次数
常数项
概念
项
