11.1.2 三角形的高、中线与角平分线&11.1.3 三角形的稳定性 课件(共28张PPT) 2023—2024学年人教版数学八年级上册
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线&11.1.3 三角形的稳定性 课件(共28张PPT) 2023—2024学年人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 860.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 08:59:57 | ||
图片预览






文档简介
(共28张PPT)
八年级·数学·人教版·上册
11.1 与三角形有关的线段
11.1.3 三角形的稳定性
1.知道三角形的高、中线与角平分线的意义,并能熟练地画出任意三角形的高、中线与角平分线.
2.能应用三角形的高、中线和角平分线的性质进行简单的计算.
3.知道三角形的稳定性.
◎重点:三角形的高、中线和角平分线的定义及画法.
◎难点:作钝角三角形的高.
【课前准备】三角尺、自制三角形木架、四边形木架.
生活中哪些物体的结构是三角形 学生回答:房梁、建筑工地的脚手架、自行车车架、乐谱架、起重机的吊臂等.你知道为什么把它们设计成三角形吗
设置情境问题,激发学生的兴趣,让学生探索三角形的重要线段及明确三角形的稳定性.
三角形的中线、高线、角平分线
阅读课本11.1.2的内容,完成下列问题.(阅读时注意思考:三角形的中线、高线、角平分线是直线、射线还是线段)
1.填表.
定义 图形 应用
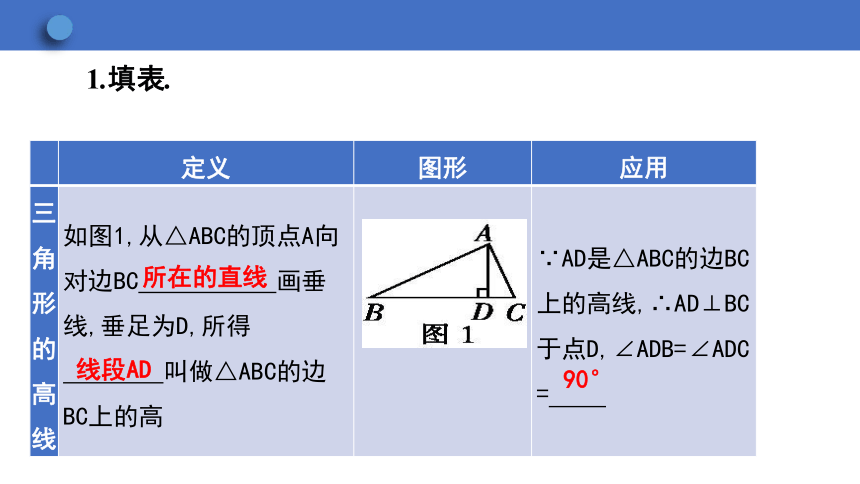
三角形的高线 如图1,从△ABC的顶点A向对边BC 画垂线,垂足为D,所得 叫做△ABC的边BC上的高 ∵AD是△ABC的边BC上的高线,∴AD⊥BC于点D,∠ADB=∠ADC
=
所在的直线
线段AD
90°
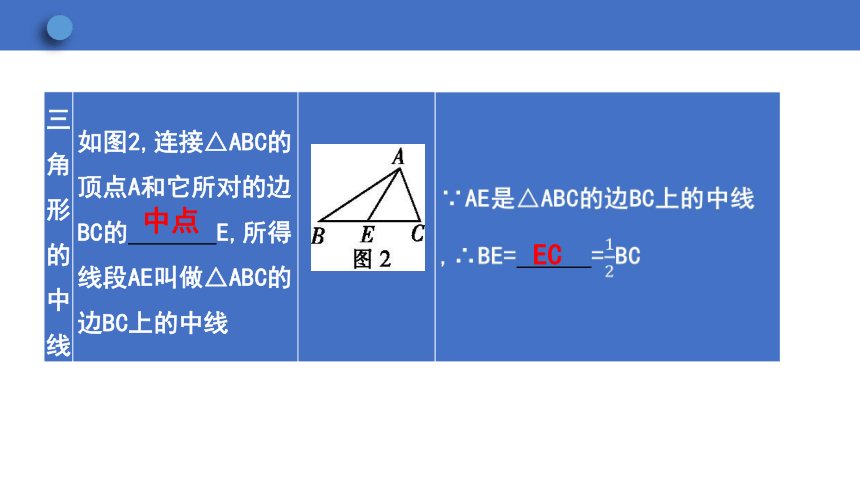
三角形的中线 如图2,连接△ABC的顶点A和它所对的边BC的 E,所得线段AE叫做△ABC的边BC上的中线 ∵AE是△ABC的边BC上的中线,∴BE= =BC
中点
EC
定义 图形 应用
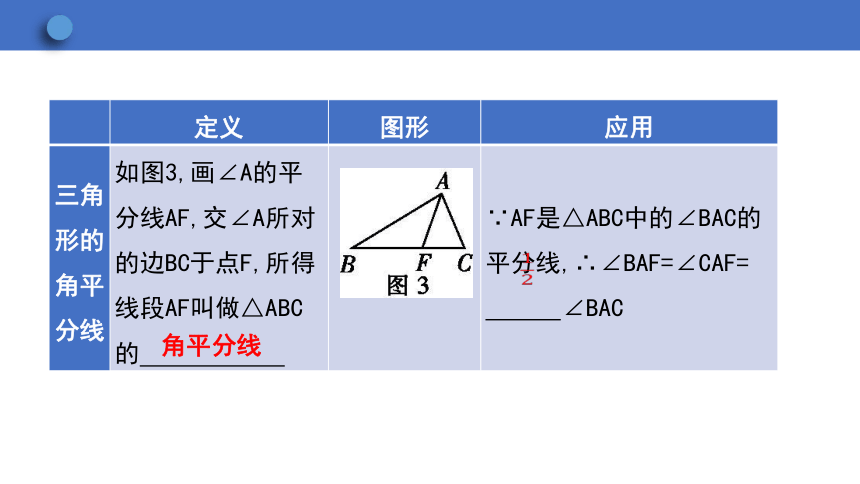
三角形的角平分线 如图3,画∠A的平分线AF,交∠A所对的边BC于点F,所得线段AF叫做△ABC的 ∵AF是△ABC中的∠BAC的平分线,∴∠BAF=∠CAF=
∠BAC
角平分线
·设计意图·
将三角形的中线、高、角平分线,用表格的形式表示出来,使它们的三种语言(文字、图形、数学符号)相结合,便于理解和区分.
2.三角形的三条中线相交于一点,这点叫做三角形的
.
重心
【讨论】上表中的图2,△ABE与△AEC的面积有什么关系 为什么
答:面积相等;因为等底同高.
·导学建议·
1.对于三角形的三条重要线段,可先让学生画图实践,再让他们相互交流画图感受,然后师生共同归纳.
2.对于三角形的高线,可让学生分别画出锐角三角形、直角三角形和钝角三角形的高.通过画图,让学生感知钝角三角形有一条高在三角形内,两条高在三角形外.对于直角三角形,有些学生会误认为直角三角形只能画斜边上的一条高,教师要给予说明三角形两条直角边也是这个三角形的高.
三角形的稳定性
阅读课本11.1.3的内容,解决下列问题.
·导学建议·
教师可让一个学生到讲台演示:1.扭动自制的三角形木架;2.扭动自制的四边形木架.
星期天,小强和爸爸用木头制作了一个长方形的大门(如图所示),但他发现这个大门摇晃、不稳定,于是小强再在木门的背面加钉了一根木条,这样做的道理是因为四边形具有
,而三角形具有 .
稳定性
不稳定性
1.三角形的角平分线、中线以及高都是 ( )
A.射线 B.直线 C.线段 D.以上都不对
C
2.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是 ( )
A.BF=CF
B.∠C+∠CAD=90°
C.∠BAF=∠CAF
D.S△ABC=2S△ABF
C
3.如图,AD⊥BC于点D,则图中以AD为其中一条高的三角形有 个.
6
识别三角形的高
1.如图,△ABC中边BC上的高是 ,△ACD中边CD上的高是 ,△BCE中边BC上的高是 ,以CF为高的三角形是
.
△ABC、△BCF、△ACF
AD
AD
EB
方法归纳交流 作钝角三角形的高时,钝角所在的两条边上的高一定在三角形的 ,而且要与指定的边 .
垂直
外部
利用三角形的面积求高
2.若在△ABC中,∠B=90°,AB=3,BC=4,AC=5,则AC边上的高为 .
方法归纳交流 当三角形中有高出现时,可考虑借助
解决问题.
稳定性的实际应用
3.如图,人字梯中间一般会设计一“拉杆”,这样做的道理是 ( )
A.三角形的任意两边之和大于第三边
B.两点确定一条直线
C.三角形具有稳定性
D.垂线段最短
C
利用三角形的中线求线段的长
4.在△ABC中, AD是BC边上的中线,△ABD的周长比△ACD的周长小5 cm,请你求出AC与AB的长度差.
解:因为△ABD的周长比△ACD的周长小5 cm.
所以(AC+AD+CD)-(AB+BD+AD)=5 cm,即AC-AB+CD-BD=5 cm.
因为AD是BC边上的中线,所以BD=CD,所以AC-AB=5 cm.
即AC与AB的长度差为5 cm.
如图,这是一块三角形优良品种试验田,现引进四种不同的种子进行对比试验,需要将这块地分成面积相等的四块.请你设计出划分方案,画图说明.
解:方法不唯一,如图,D、E、F是BC边的四等分点;O、P、Q分别是AB、BC、CA边的中点.
1.下列图形具有稳定性的是 ( )
A B C D
A
2.下列说法中错误的是 ( )
A.三角形的高、中线、角平分线都是线段
B.三角形的三条中线都在三角形内部
C.锐角三角形的三条高一定交于同一点
D.三角形的三条高、三条中线、三条角平分线都交于同一点
D
3.
如图,D是△ABC中BC上的一点,DE∥AC交AB于点E,DF∥AB交AC于点F,且∠ADE=∠ADF,AD是△ABC的角平分线吗 请说明理由.
解:AD是△ABC的角平分线.
理由:∵DE∥AC,DF∥AB,∴∠ADE=∠DAF,∠ADF=∠DAE.
又∵∠ADE=∠ADF,∴∠DAF=∠DAE,
∴AD是△BAC的角平分线.
八年级·数学·人教版·上册
11.1 与三角形有关的线段
11.1.3 三角形的稳定性
1.知道三角形的高、中线与角平分线的意义,并能熟练地画出任意三角形的高、中线与角平分线.
2.能应用三角形的高、中线和角平分线的性质进行简单的计算.
3.知道三角形的稳定性.
◎重点:三角形的高、中线和角平分线的定义及画法.
◎难点:作钝角三角形的高.
【课前准备】三角尺、自制三角形木架、四边形木架.
生活中哪些物体的结构是三角形 学生回答:房梁、建筑工地的脚手架、自行车车架、乐谱架、起重机的吊臂等.你知道为什么把它们设计成三角形吗
设置情境问题,激发学生的兴趣,让学生探索三角形的重要线段及明确三角形的稳定性.
三角形的中线、高线、角平分线
阅读课本11.1.2的内容,完成下列问题.(阅读时注意思考:三角形的中线、高线、角平分线是直线、射线还是线段)
1.填表.
定义 图形 应用
三角形的高线 如图1,从△ABC的顶点A向对边BC 画垂线,垂足为D,所得 叫做△ABC的边BC上的高 ∵AD是△ABC的边BC上的高线,∴AD⊥BC于点D,∠ADB=∠ADC
=
所在的直线
线段AD
90°
三角形的中线 如图2,连接△ABC的顶点A和它所对的边BC的 E,所得线段AE叫做△ABC的边BC上的中线 ∵AE是△ABC的边BC上的中线,∴BE= =BC
中点
EC
定义 图形 应用
三角形的角平分线 如图3,画∠A的平分线AF,交∠A所对的边BC于点F,所得线段AF叫做△ABC的 ∵AF是△ABC中的∠BAC的平分线,∴∠BAF=∠CAF=
∠BAC
角平分线
·设计意图·
将三角形的中线、高、角平分线,用表格的形式表示出来,使它们的三种语言(文字、图形、数学符号)相结合,便于理解和区分.
2.三角形的三条中线相交于一点,这点叫做三角形的
.
重心
【讨论】上表中的图2,△ABE与△AEC的面积有什么关系 为什么
答:面积相等;因为等底同高.
·导学建议·
1.对于三角形的三条重要线段,可先让学生画图实践,再让他们相互交流画图感受,然后师生共同归纳.
2.对于三角形的高线,可让学生分别画出锐角三角形、直角三角形和钝角三角形的高.通过画图,让学生感知钝角三角形有一条高在三角形内,两条高在三角形外.对于直角三角形,有些学生会误认为直角三角形只能画斜边上的一条高,教师要给予说明三角形两条直角边也是这个三角形的高.
三角形的稳定性
阅读课本11.1.3的内容,解决下列问题.
·导学建议·
教师可让一个学生到讲台演示:1.扭动自制的三角形木架;2.扭动自制的四边形木架.
星期天,小强和爸爸用木头制作了一个长方形的大门(如图所示),但他发现这个大门摇晃、不稳定,于是小强再在木门的背面加钉了一根木条,这样做的道理是因为四边形具有
,而三角形具有 .
稳定性
不稳定性
1.三角形的角平分线、中线以及高都是 ( )
A.射线 B.直线 C.线段 D.以上都不对
C
2.如图,在△ABC中,AD是高,AE是角平分线,AF是中线,则下列说法中错误的是 ( )
A.BF=CF
B.∠C+∠CAD=90°
C.∠BAF=∠CAF
D.S△ABC=2S△ABF
C
3.如图,AD⊥BC于点D,则图中以AD为其中一条高的三角形有 个.
6
识别三角形的高
1.如图,△ABC中边BC上的高是 ,△ACD中边CD上的高是 ,△BCE中边BC上的高是 ,以CF为高的三角形是
.
△ABC、△BCF、△ACF
AD
AD
EB
方法归纳交流 作钝角三角形的高时,钝角所在的两条边上的高一定在三角形的 ,而且要与指定的边 .
垂直
外部
利用三角形的面积求高
2.若在△ABC中,∠B=90°,AB=3,BC=4,AC=5,则AC边上的高为 .
方法归纳交流 当三角形中有高出现时,可考虑借助
解决问题.
稳定性的实际应用
3.如图,人字梯中间一般会设计一“拉杆”,这样做的道理是 ( )
A.三角形的任意两边之和大于第三边
B.两点确定一条直线
C.三角形具有稳定性
D.垂线段最短
C
利用三角形的中线求线段的长
4.在△ABC中, AD是BC边上的中线,△ABD的周长比△ACD的周长小5 cm,请你求出AC与AB的长度差.
解:因为△ABD的周长比△ACD的周长小5 cm.
所以(AC+AD+CD)-(AB+BD+AD)=5 cm,即AC-AB+CD-BD=5 cm.
因为AD是BC边上的中线,所以BD=CD,所以AC-AB=5 cm.
即AC与AB的长度差为5 cm.
如图,这是一块三角形优良品种试验田,现引进四种不同的种子进行对比试验,需要将这块地分成面积相等的四块.请你设计出划分方案,画图说明.
解:方法不唯一,如图,D、E、F是BC边的四等分点;O、P、Q分别是AB、BC、CA边的中点.
1.下列图形具有稳定性的是 ( )
A B C D
A
2.下列说法中错误的是 ( )
A.三角形的高、中线、角平分线都是线段
B.三角形的三条中线都在三角形内部
C.锐角三角形的三条高一定交于同一点
D.三角形的三条高、三条中线、三条角平分线都交于同一点
D
3.
如图,D是△ABC中BC上的一点,DE∥AC交AB于点E,DF∥AB交AC于点F,且∠ADE=∠ADF,AD是△ABC的角平分线吗 请说明理由.
解:AD是△ABC的角平分线.
理由:∵DE∥AC,DF∥AB,∴∠ADE=∠DAF,∠ADF=∠DAE.
又∵∠ADE=∠ADF,∴∠DAF=∠DAE,
∴AD是△BAC的角平分线.
