11.2.1 第1课时 三角形的内角和 课件(共29张PPT)2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 11.2.1 第1课时 三角形的内角和 课件(共29张PPT)2023-2024学年人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 731.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
八年级·数学·人教版·上册
11.2 与三角形有关的角
11.2.1 三角形的内角
第1课时 三角形的内角和(见学生用书P6)
1.会证明三角形内角和等于180°,学会规范的推理过程.
2.会应用三角形内角和定理解决一些简单的实际问题.
3.通过探索证明三角形内角和定理的活动,增强论证能力,拓宽解题思路.
◎重点:利用三角形内角和定理解答简单的数学问题.
◎难点:三角形内角和定理的探究过程.
【课前准备】每人准备一个由硬纸片剪出的三角形.
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行呀!”老大说,“这是不可能的,否则,我们这个家就再也围不起来了.”老二很纳闷地说:“为什么 ”
你们知道其中的道理吗
通过设置趣味情境问题,引导学生产生兴趣,探讨三角形内角和定理.
三角形内角和定理
阅读课本本节开始至“例1”结束,解决下列问题.
操作探究:请你将课前准备好的三角形纸片的三个内角剪下,拼在一起,看看能否拼成180°.
结论巩固 三角形的内角和等于 ,证明时常通过添加
构造平角、同旁内角建立起三个角之间的关系.在△ABC中,若已知∠A、∠B,则∠C= .
平行线
180°
180°-∠A-∠B
·导学建议·
先让学生动手操作,通过测量感受“三角形内角和是180°”,再让学生用几何方法进行证明.证明时可以让学生展示不同的证明方法.
三角形内角和定理的实际应用
阅读课本“例2”,解决下列问题.
例题也可以过点C作CF∥AD交AB于点F,则∠ACF=
.又因为AD∥BE,所以CF∥ ,所以∠BCF=
,所以∠ACB=∠ACF+∠BCF= +
= .
归纳总结 在求角的度数时,常找出三角形各角之间的关系,列出等式,求出角的度数.
90°
∠DAC
BE
∠CBE
∠DAC
∠CBE
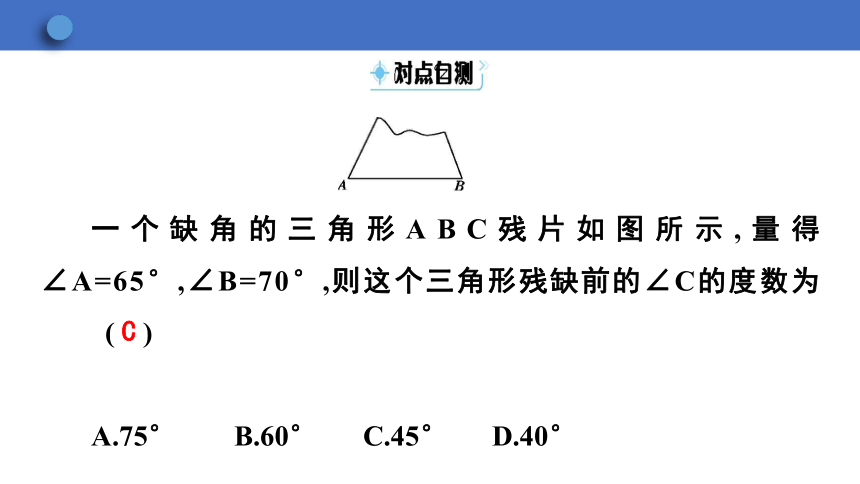
一个缺角的三角形ABC残片如图所示,量得∠A=65°,∠B=70°,则这个三角形残缺前的∠C的度数为 ( )
A.75° B.60° C.45° D.40°
C
·真实情境·
《2022年版数学课程标准》中指出:情境创设的真实性.本题以生活中常见的残片三角形为背景,将三角形的内角和融入其中.
2.在△ABC中,若∠B=∠C=2∠A,则∠A的度数为 ( )
A.72° B.45° C.36° D.30°
C
3.
如图,这是A、B、C三个村庄的平面图,已知B村在A村的南偏西65°15'方向,C村在A村的南偏东15°方向,C村在B村的北偏东85°方向,求从C村观测A、B两村的视角∠ACB的度数.
解:由题意得∠BAC=65°15'+15°=80°15',∠ABC=85°-65°15'=19°45'.
在△ABC中,∠ACB=180°-∠BAC-∠ABC=180°-80°15'-19°45'=80°.
1.如图,在△ABC中,∠A=50°,∠ABC、∠ACB的平分线交于点O,则∠BOC等于 ( )
A.65° B.115°
C.80° D.50°
B
变式演练 在任务驱动一中,若∠A=α,则∠BOC=
(用含α的式子表示).
90°+α
2.在△ABC中,∠A-∠B=30°,∠C=4∠B.求∠A、∠B、∠C的度数.
·设题目的·
根据三角形内角和定理构造方程解决问题.
·解题关键点·
先设一个角的度数为x°,再根据条件用x的式子表示另两个角的度数,利用三角形内角和定理列方程,解方程使问题得到解决.
解:设∠B=x°,则∠A=(30+x)°,∠C=4x°.
由三角形内角和定理得30+x+x+4x=180,解得x=25,∴∠A=55°,∠B=25°,∠C=100°.
方法归纳交流 当已知三角形三个内角之间的数量关系时,可由三角形内角和定理用 的方法求出各角的度数.
列方程(组)
·导学建议·
在求三角形内角时,三角形内角和等于180°容易被学生忽略,应提醒学生注意.
3.如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,则∠ADE的大小是 ( )
A.30° B.40° C.50° D.60°
B
如图,在△ABC中,AD是高,AE、BF是角平分线,交于点O,∠BAC=60°,∠C=70°,求∠CAD与∠BOA的度数.
解:因为AD是高,所以∠ADC=90°,所以∠CAD=180°-∠ADC-∠C=20°.因为∠BAC=60°,∠C=70°,所以∠ABC=180°-∠BAC -∠C=50°.因为AE是∠BAC的平分线,所以∠BAO=30°,同理∠ABO=25°,所以∠BOA=180°-∠BAO-∠ABO=125°.
如图,在△ABC中,AD是△ABC的角平分线,DE⊥AC.若∠B=40°,∠C=60°,则∠ADE的度数为 ( )
A.30° B.40°
C.50° D.60°
C
2.若三角形三个内角度数的比为1∶2∶3,则这个三角形的最小角的度数是 .
30°
3.如图,在△ABC中,∠BAC=100°,AD⊥BC于点D,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 .
14°
4.如图,已知D为△ABC边BC延长线上的一点,DF⊥AB于点F,交AC于点E,若∠A=35°,∠D=42°,则∠ACD的度数为
.
83°
5.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AD于点E.若∠C=75°,∠BED=65°,求∠BAC的度数.
解:∵AD是BC边上的高,∴∠BDE=90°.
在△BDE中,∠BED=65°,∠BDE=90°,
∴∠DBE=180°-∠BED-∠BDE=180°-65°-90°=25°.
∵BE平分∠ABC,∴∠ABC=2∠DBE=2×25°=50°.
在△ABC中,∠ABC=50°,∠C=75°,∴∠BAC=180°-∠ABC-∠C=180°-50°-75°=55°.
八年级·数学·人教版·上册
11.2 与三角形有关的角
11.2.1 三角形的内角
第1课时 三角形的内角和(见学生用书P6)
1.会证明三角形内角和等于180°,学会规范的推理过程.
2.会应用三角形内角和定理解决一些简单的实际问题.
3.通过探索证明三角形内角和定理的活动,增强论证能力,拓宽解题思路.
◎重点:利用三角形内角和定理解答简单的数学问题.
◎难点:三角形内角和定理的探究过程.
【课前准备】每人准备一个由硬纸片剪出的三角形.
在一个直角三角形里住着三个内角,平时,它们三兄弟非常团结.可是有一天,老二突然不高兴,发起脾气来,它指着老大说:“你凭什么度数最大,我也要和你一样大!”“不行呀!”老大说,“这是不可能的,否则,我们这个家就再也围不起来了.”老二很纳闷地说:“为什么 ”
你们知道其中的道理吗
通过设置趣味情境问题,引导学生产生兴趣,探讨三角形内角和定理.
三角形内角和定理
阅读课本本节开始至“例1”结束,解决下列问题.
操作探究:请你将课前准备好的三角形纸片的三个内角剪下,拼在一起,看看能否拼成180°.
结论巩固 三角形的内角和等于 ,证明时常通过添加
构造平角、同旁内角建立起三个角之间的关系.在△ABC中,若已知∠A、∠B,则∠C= .
平行线
180°
180°-∠A-∠B
·导学建议·
先让学生动手操作,通过测量感受“三角形内角和是180°”,再让学生用几何方法进行证明.证明时可以让学生展示不同的证明方法.
三角形内角和定理的实际应用
阅读课本“例2”,解决下列问题.
例题也可以过点C作CF∥AD交AB于点F,则∠ACF=
.又因为AD∥BE,所以CF∥ ,所以∠BCF=
,所以∠ACB=∠ACF+∠BCF= +
= .
归纳总结 在求角的度数时,常找出三角形各角之间的关系,列出等式,求出角的度数.
90°
∠DAC
BE
∠CBE
∠DAC
∠CBE
一个缺角的三角形ABC残片如图所示,量得∠A=65°,∠B=70°,则这个三角形残缺前的∠C的度数为 ( )
A.75° B.60° C.45° D.40°
C
·真实情境·
《2022年版数学课程标准》中指出:情境创设的真实性.本题以生活中常见的残片三角形为背景,将三角形的内角和融入其中.
2.在△ABC中,若∠B=∠C=2∠A,则∠A的度数为 ( )
A.72° B.45° C.36° D.30°
C
3.
如图,这是A、B、C三个村庄的平面图,已知B村在A村的南偏西65°15'方向,C村在A村的南偏东15°方向,C村在B村的北偏东85°方向,求从C村观测A、B两村的视角∠ACB的度数.
解:由题意得∠BAC=65°15'+15°=80°15',∠ABC=85°-65°15'=19°45'.
在△ABC中,∠ACB=180°-∠BAC-∠ABC=180°-80°15'-19°45'=80°.
1.如图,在△ABC中,∠A=50°,∠ABC、∠ACB的平分线交于点O,则∠BOC等于 ( )
A.65° B.115°
C.80° D.50°
B
变式演练 在任务驱动一中,若∠A=α,则∠BOC=
(用含α的式子表示).
90°+α
2.在△ABC中,∠A-∠B=30°,∠C=4∠B.求∠A、∠B、∠C的度数.
·设题目的·
根据三角形内角和定理构造方程解决问题.
·解题关键点·
先设一个角的度数为x°,再根据条件用x的式子表示另两个角的度数,利用三角形内角和定理列方程,解方程使问题得到解决.
解:设∠B=x°,则∠A=(30+x)°,∠C=4x°.
由三角形内角和定理得30+x+x+4x=180,解得x=25,∴∠A=55°,∠B=25°,∠C=100°.
方法归纳交流 当已知三角形三个内角之间的数量关系时,可由三角形内角和定理用 的方法求出各角的度数.
列方程(组)
·导学建议·
在求三角形内角时,三角形内角和等于180°容易被学生忽略,应提醒学生注意.
3.如图,在△ABC中,∠B+∠C=100°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,则∠ADE的大小是 ( )
A.30° B.40° C.50° D.60°
B
如图,在△ABC中,AD是高,AE、BF是角平分线,交于点O,∠BAC=60°,∠C=70°,求∠CAD与∠BOA的度数.
解:因为AD是高,所以∠ADC=90°,所以∠CAD=180°-∠ADC-∠C=20°.因为∠BAC=60°,∠C=70°,所以∠ABC=180°-∠BAC -∠C=50°.因为AE是∠BAC的平分线,所以∠BAO=30°,同理∠ABO=25°,所以∠BOA=180°-∠BAO-∠ABO=125°.
如图,在△ABC中,AD是△ABC的角平分线,DE⊥AC.若∠B=40°,∠C=60°,则∠ADE的度数为 ( )
A.30° B.40°
C.50° D.60°
C
2.若三角形三个内角度数的比为1∶2∶3,则这个三角形的最小角的度数是 .
30°
3.如图,在△ABC中,∠BAC=100°,AD⊥BC于点D,AE平分∠BAC交BC于点E.若∠C=26°,则∠DAE的度数为 .
14°
4.如图,已知D为△ABC边BC延长线上的一点,DF⊥AB于点F,交AC于点E,若∠A=35°,∠D=42°,则∠ACD的度数为
.
83°
5.如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AD于点E.若∠C=75°,∠BED=65°,求∠BAC的度数.
解:∵AD是BC边上的高,∴∠BDE=90°.
在△BDE中,∠BED=65°,∠BDE=90°,
∴∠DBE=180°-∠BED-∠BDE=180°-65°-90°=25°.
∵BE平分∠ABC,∴∠ABC=2∠DBE=2×25°=50°.
在△ABC中,∠ABC=50°,∠C=75°,∴∠BAC=180°-∠ABC-∠C=180°-50°-75°=55°.
