11.2.2 三角形的外角 课件(共31张PPT)2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 11.2.2 三角形的外角 课件(共31张PPT)2023-2024学年人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 788.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 09:03:43 | ||
图片预览











文档简介
(共31张PPT)
八年级·数学·人教版·上册
11.2 与三角形有关的角
11.2.2 三角形的外角
1.知道三角形外角的概念,会识别三角形的外角.
2.会证明三角形的外角的性质,并能运用这些性质解决简单的问题.
◎重点:三角形外角的性质及应用.
◎难点:三角形外角性质的应用.
如图,两只猎豹在A处发现有一只离群的野牛独自在O处觅食,猎豹打算用迂回的方式,由一只先从A前进到C处,然后再折回到B处截住野牛返回牛群的去路,另一只则直接从A处扑向野牛,已知∠BAC=40°,∠ABC=70°,问:猎豹从 C处要转多少度才能直达B处
三角形的外角
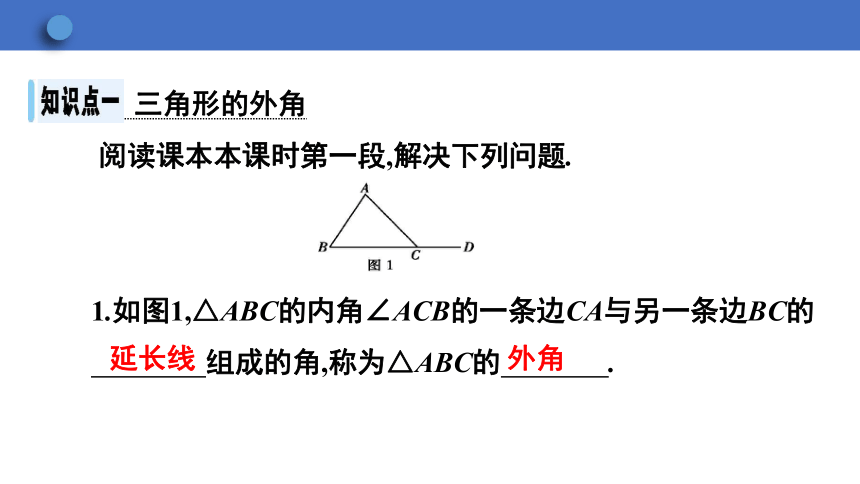
阅读课本本课时第一段,解决下列问题.
1.如图1,△ABC的内角∠ACB的一条边CA与另一条边BC的
组成的角,称为△ABC的 .
外角
延长线
2.画出一个三角形的外角,你能回答下列问题吗
(1)每个三角形有几个外角
(2)每一个顶点处相对应的外角有几个
(3)三角形每一个顶点处的外角与内角有什么关系
答:(1)每个三角形有6个外角;(2)每一个顶点处相对应的外角有2个;(3)三角形每一个顶点处的外角与内角互补.
·导学建议·
可提出问题:“如图1,△ABC的顶点C处可以画出几个外角 它们有什么关系 ”学生画图,给出结论.通过画图,使学生明白三角形某个顶点处有两个外角,它们互为对顶角.
三角形的外角的性质
阅读课本本课时“思考”至结束,解决下列问题.
1.如图1,完成如下证明过程:
证明:在△ABC中,∵∠A+∠B+∠ACB= (
),∠ACB+∠ACD= (
),∴∠ACD= + .
三角形内角和定理
180°
∠A
180°
平角的定义
∠B
2.三角形每个顶点处取一个外角,则三角形的外角和等于
.
360°
归纳总结 三角形的一个外角等于
的和.
与它不相邻的两个内角
【讨论】有同学将三角形内角和定理的推论用语言归纳为“三角形的一个外角等于两个内角的和,它也大于三角形的一个内角.”你认为他的说法对吗 为什么
答:不对,推论中必须加上“不相邻”这几个字.
·导学建议·
在归纳三角形外角的性质时,学生可能会出现“三角形的一个外角等于两个内角的和”的错误理解,可借助图形帮助学生理解关键字“不相邻”的重要性.
1.如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A的度数为 ( )
A.40° B.50° C.55° D.60°
D
2.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
C
3.如图,∠DBA=105°,∠ECA=125°,则∠A的度数为
.
50°
1.如图,∠1、∠2、∠3的大小关系为 ( )
A.∠2>∠1>∠3
B.∠1>∠3>∠2
C.∠3>∠2>∠1
D.∠1>∠2>∠3
D
方法归纳交流 三角形中比较两个角的大小常用的方法有:
通过求角的度数比较或利用三角形的外角大于任意一个与它不相邻的内角这一性质比较
2.如图,∠A=65°,∠B=75°,将△ABC沿EF折叠,使点C落到点C'处,若∠1=20°,则∠2= .
60°
连接CC',根据三角形外角的性质,可知∠1=
+ ,∠2= + ,故∠1+∠2= + .
∠C'
∠ACC'
∠EC'C
∠BCC'
∠FC'C
∠C
·导学建议·
可让学生通过不同方法求解(方法1:利用三角形的内角和;方法2:利用三角形的外角的性质 ),然后让学生比较、评价两种解法哪一种更简单.
3.(方法指导:添加辅助线,由三角形的内角和定理的推论求几个角之间的关系)如图,求证:∠BDC=∠B+∠C+∠BAC.
证明:如图,连接AD并延长至点E,则∠BDC=∠BDE+∠CDE,
而∠BDE=∠B+∠BAD,∠CDE=∠C+∠CAD,∴∠BDE+∠CDE=∠B+∠C+∠BAD+∠CAD,即∠BDC=∠B+∠C+∠BAC.
(证法不唯一,也可以通过连接BC证得)
·设计意图·
据不同的添加辅助线的方法,开拓学生的思维能力,培养一题多证的思维品质.
4.如图, D是BC延长线上一点,∠ABC、∠ACD的平分线交于点E,试探究∠E与∠A有何数量关系,并证明.
解:∠E=∠A.
证明:因为∠ABC、∠ACD的平分线交于点E,
所以∠ECD=∠ACD,∠EBC=∠ABC.
因为∠E=∠ECD-∠EBC,∠A=∠ACD-∠ABC,
所以∠E=(∠ACD-∠ABC)=∠A.
方法归纳交流 在三角形的计算中,常借助三角形的内角和定理联系 角之间的关系解决问题.
内、外
如图,将一副直角三角板这样放置,使两直角重合,则∠DFB的度数为 ( )
A.145° B.155°
C.165° D.175°
C
2.在△ABC中,∠A=x°,∠B=(2x+10)°,∠C的外角大小为(x+40)°,则x的值等于 ( )
A.15 B.20 C.30 D.40
A
3.
如图,在△ABC中,∠ABC=∠ACB,∠A=36°,P是△ABC内一点,且∠1=∠2,则∠BPC的度数为 .
108°
4.
如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)如果∠B=35°,∠E=20°,求∠BAC的度数.
(2)求证:∠BAC=∠B+2∠E.
解:(1)∵∠B=35°,∠E=20°,∴∠ECD=∠B+∠E=55°.
∵CE是△ABC的外角∠ACD的平分线,
∴∠ACD=2∠ECD=110°,
∴∠BAC=∠ACD-∠B=75°.
(2)证明:∵CE平分∠ACD,∴∠ACE=∠DCE.
∵∠DCE=∠B+∠E,∴∠ACE=∠B+∠E.
∵∠BAC=∠ACE+∠E,∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
八年级·数学·人教版·上册
11.2 与三角形有关的角
11.2.2 三角形的外角
1.知道三角形外角的概念,会识别三角形的外角.
2.会证明三角形的外角的性质,并能运用这些性质解决简单的问题.
◎重点:三角形外角的性质及应用.
◎难点:三角形外角性质的应用.
如图,两只猎豹在A处发现有一只离群的野牛独自在O处觅食,猎豹打算用迂回的方式,由一只先从A前进到C处,然后再折回到B处截住野牛返回牛群的去路,另一只则直接从A处扑向野牛,已知∠BAC=40°,∠ABC=70°,问:猎豹从 C处要转多少度才能直达B处
三角形的外角
阅读课本本课时第一段,解决下列问题.
1.如图1,△ABC的内角∠ACB的一条边CA与另一条边BC的
组成的角,称为△ABC的 .
外角
延长线
2.画出一个三角形的外角,你能回答下列问题吗
(1)每个三角形有几个外角
(2)每一个顶点处相对应的外角有几个
(3)三角形每一个顶点处的外角与内角有什么关系
答:(1)每个三角形有6个外角;(2)每一个顶点处相对应的外角有2个;(3)三角形每一个顶点处的外角与内角互补.
·导学建议·
可提出问题:“如图1,△ABC的顶点C处可以画出几个外角 它们有什么关系 ”学生画图,给出结论.通过画图,使学生明白三角形某个顶点处有两个外角,它们互为对顶角.
三角形的外角的性质
阅读课本本课时“思考”至结束,解决下列问题.
1.如图1,完成如下证明过程:
证明:在△ABC中,∵∠A+∠B+∠ACB= (
),∠ACB+∠ACD= (
),∴∠ACD= + .
三角形内角和定理
180°
∠A
180°
平角的定义
∠B
2.三角形每个顶点处取一个外角,则三角形的外角和等于
.
360°
归纳总结 三角形的一个外角等于
的和.
与它不相邻的两个内角
【讨论】有同学将三角形内角和定理的推论用语言归纳为“三角形的一个外角等于两个内角的和,它也大于三角形的一个内角.”你认为他的说法对吗 为什么
答:不对,推论中必须加上“不相邻”这几个字.
·导学建议·
在归纳三角形外角的性质时,学生可能会出现“三角形的一个外角等于两个内角的和”的错误理解,可借助图形帮助学生理解关键字“不相邻”的重要性.
1.如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A的度数为 ( )
A.40° B.50° C.55° D.60°
D
2.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是 ( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
C
3.如图,∠DBA=105°,∠ECA=125°,则∠A的度数为
.
50°
1.如图,∠1、∠2、∠3的大小关系为 ( )
A.∠2>∠1>∠3
B.∠1>∠3>∠2
C.∠3>∠2>∠1
D.∠1>∠2>∠3
D
方法归纳交流 三角形中比较两个角的大小常用的方法有:
通过求角的度数比较或利用三角形的外角大于任意一个与它不相邻的内角这一性质比较
2.如图,∠A=65°,∠B=75°,将△ABC沿EF折叠,使点C落到点C'处,若∠1=20°,则∠2= .
60°
连接CC',根据三角形外角的性质,可知∠1=
+ ,∠2= + ,故∠1+∠2= + .
∠C'
∠ACC'
∠EC'C
∠BCC'
∠FC'C
∠C
·导学建议·
可让学生通过不同方法求解(方法1:利用三角形的内角和;方法2:利用三角形的外角的性质 ),然后让学生比较、评价两种解法哪一种更简单.
3.(方法指导:添加辅助线,由三角形的内角和定理的推论求几个角之间的关系)如图,求证:∠BDC=∠B+∠C+∠BAC.
证明:如图,连接AD并延长至点E,则∠BDC=∠BDE+∠CDE,
而∠BDE=∠B+∠BAD,∠CDE=∠C+∠CAD,∴∠BDE+∠CDE=∠B+∠C+∠BAD+∠CAD,即∠BDC=∠B+∠C+∠BAC.
(证法不唯一,也可以通过连接BC证得)
·设计意图·
据不同的添加辅助线的方法,开拓学生的思维能力,培养一题多证的思维品质.
4.如图, D是BC延长线上一点,∠ABC、∠ACD的平分线交于点E,试探究∠E与∠A有何数量关系,并证明.
解:∠E=∠A.
证明:因为∠ABC、∠ACD的平分线交于点E,
所以∠ECD=∠ACD,∠EBC=∠ABC.
因为∠E=∠ECD-∠EBC,∠A=∠ACD-∠ABC,
所以∠E=(∠ACD-∠ABC)=∠A.
方法归纳交流 在三角形的计算中,常借助三角形的内角和定理联系 角之间的关系解决问题.
内、外
如图,将一副直角三角板这样放置,使两直角重合,则∠DFB的度数为 ( )
A.145° B.155°
C.165° D.175°
C
2.在△ABC中,∠A=x°,∠B=(2x+10)°,∠C的外角大小为(x+40)°,则x的值等于 ( )
A.15 B.20 C.30 D.40
A
3.
如图,在△ABC中,∠ABC=∠ACB,∠A=36°,P是△ABC内一点,且∠1=∠2,则∠BPC的度数为 .
108°
4.
如图,CE是△ABC的外角∠ACD的平分线,且CE交BA的延长线于点E.
(1)如果∠B=35°,∠E=20°,求∠BAC的度数.
(2)求证:∠BAC=∠B+2∠E.
解:(1)∵∠B=35°,∠E=20°,∴∠ECD=∠B+∠E=55°.
∵CE是△ABC的外角∠ACD的平分线,
∴∠ACD=2∠ECD=110°,
∴∠BAC=∠ACD-∠B=75°.
(2)证明:∵CE平分∠ACD,∴∠ACE=∠DCE.
∵∠DCE=∠B+∠E,∴∠ACE=∠B+∠E.
∵∠BAC=∠ACE+∠E,∴∠BAC=∠B+∠E+∠E=∠B+2∠E.
