11.3.2 多边形的内角和 课件(共31张PPT)2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 11.3.2 多边形的内角和 课件(共31张PPT)2023-2024学年人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 792.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 09:07:30 | ||
图片预览









文档简介
(共31张PPT)
八年级·数学·人教版·上册
11.3 多边形及其内角和
11.3.2 多边形的内角和
1.会通过不同方法探索多边形的内角和与外角和公式,并会用它们进行有关计算.
2.通过将多边形问题转化为三角形问题解决,体会化归思想的应用方法,提高分析问题和解决问题的能力.
◎重点:多边形的内角和与外角和.
◎难点:多边形的内角和公式的推导.
可用多媒体出示一组由多边形组合成的美丽图案.提出问题:
1.看完这些图案你能抽象出哪些几何图形
2.生活中有如此多的几何图形,你对它们了解多少
我们知道三角形的内角和是180度,正方形、长方形的内角和是360度,那么四边形、五边形、六边形的呢
多边形的内角和
阅读课本本课时第一段至“例1”结束,解决下列问题.
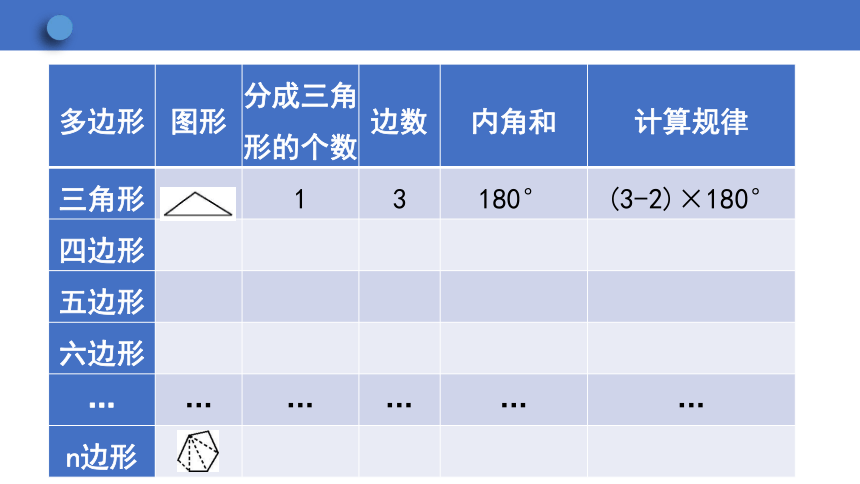
1.从多边形的一个顶点出发,可以引多少条对角线 它们将多边形分成多少个三角形 填写下表:
多边形 图形 分成三角 形的个数 边数 内角和 计算规律
三角形 1 3 180° (3-2)×180°
四边形
五边形
六边形
… … … … … …
n边形
解:
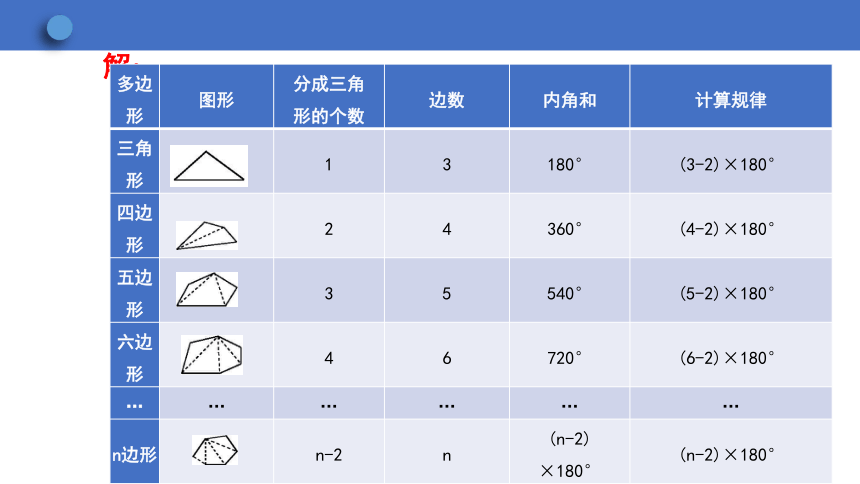
多边形 图形 分成三角 形的个数 边数 内角和 计算规律
三角形 1 3 180° (3-2)×180°
四边形 2 4 360° (4-2)×180°
五边形 3 5 540° (5-2)×180°
六边形 4 6 720° (6-2)×180°
… … … … … …
n边形 n-2 n (n-2) ×180° (n-2)×180°
·设计意图·
以表格的形式将一些简单的多边形的有关三角形、边数、内角和及计算规律列举出来,从特殊到一般找到n边形的内角和规律,培养学生的归纳能力.
2.由例题可得:如果四边形的一组对角互补,那么另一组对角 .
也互补
归纳总结 n边形的内角和等于 .
(n-2)×180°
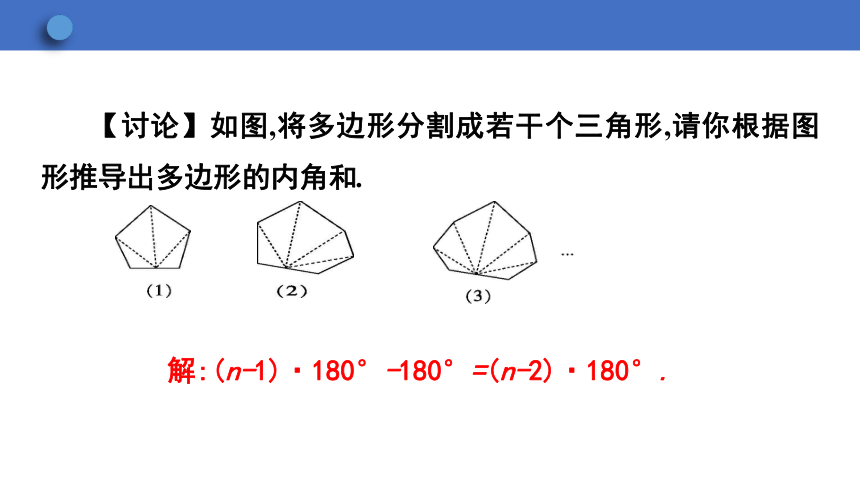
【讨论】如图,将多边形分割成若干个三角形,请你根据图形推导出多边形的内角和.
解:(n-1)·180°-180°=(n-2)·180°.
·导学建议·
可先让学生自己想,再小组交流.教师深入参与活动,必要时给予指导.可直接引导学生用添加辅助线的方法把多边形转化为三角形,最后找学生说出探索过程,其他同学补充,并说出不同观点.
多边形的外角和
阅读课本“例2”至本课时结束,仿照“例2”的探究过程,探究n(n≥3)边形的外角和.
答:因为n边形的一个外角与它相邻的内角的和是180°,n边形的n个外角加上与它相邻的内角,所得总和是n×180°,因为n边形的内角和是(n-2)×180°,∴n边形的外角和是n×180°-(n-2)×180°=360°.
归纳总结 多边形的外角和等于 .
360°
·导学建议·
预习导学部分建议用20分钟完成,以学生自主探索为主,教师巡视,必要时给予指导.
1.六边形的内角和为 ( )
A.360° B.540° C.720° D.1080°
C
2.正十二边形的一个内角的度数为 ( )
A.30° B.150° C.360° D.1800°
B
3.正十边形的每一个外角的度数为 .
36°
1.下列度数中,不可能是某个多边形的内角和的是 ( )
A.180° B.270° C.2700° D.720°
B
方法归纳交流 根据n边形内角和是(n-2)×180°可得一个多边形的内角和一定是 的倍数.
180
2.若一个四边形四个内角的度数之比为1∶3∶4∶2,则这四个内角的度数分别是 .
36°、108°、144°、72°
3.已知一个多边形的内角和是它的外角和的2倍,求这个多边形的边数.
解:设这个多边形的边数为n,则(n-2)·`180°=2×360°,解得n=6,所以这个多边形的边数是6.
4.如图,小明沿一个五边形广场的周围按逆时针方向跑步.
(1)他每跑完一圈,身体转过的角度之和是多少
(2)在图中,你能求出∠1+∠2+∠3+∠4+∠5的度数吗
·真实情境·
《2022年版数学课程标准》中指出:情境创设的真实性.本题以生活中常见的广场跑步为背景,将多边形的外角和融入其中.
解:(1)他每跑完一圈,身体转过的角度之和是360°.
(2)∠1+∠2+∠3+∠4+∠5=360°.
方法归纳交流 多边形无论边数是多少,每个顶点处取一个外角,这些外角的和都是 .
360°
1.一个多边形每一个外角都等于18°,则这个多边形的边数为 ( )
A.10 B.12 C.16 D.20
D
2.如图,在五边形ABCDE中,若去掉一个30°的角后,得到一个六边形BCDEMN,则∠1+∠2的度数为 ( )
A.210° B.110° C.150° D.100°
A
3.一个多边形的每个内角都相等,并且它的一个外角与一个内角的比为1∶3,则这个多边形为 边形.
八
4.已知两个多边形的内角总和是1800°,并且这两个多边形的边数之比为2∶5,求这两个多边形的边数.
解:设这两个多边形的边数分别为2n,5n,则180°(2n-2)+180°(5n-2)=1800°,
解得n=2,
所以2×2=4,5×2=10.
即这两个多边形的边数分别为4,10.
5.(1)如图1,图2,试研究其中∠1、∠2与∠3、∠4之间的数量关系.
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式.
解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,∴∠1+∠2=360°-(∠5+∠6),
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
八年级·数学·人教版·上册
11.3 多边形及其内角和
11.3.2 多边形的内角和
1.会通过不同方法探索多边形的内角和与外角和公式,并会用它们进行有关计算.
2.通过将多边形问题转化为三角形问题解决,体会化归思想的应用方法,提高分析问题和解决问题的能力.
◎重点:多边形的内角和与外角和.
◎难点:多边形的内角和公式的推导.
可用多媒体出示一组由多边形组合成的美丽图案.提出问题:
1.看完这些图案你能抽象出哪些几何图形
2.生活中有如此多的几何图形,你对它们了解多少
我们知道三角形的内角和是180度,正方形、长方形的内角和是360度,那么四边形、五边形、六边形的呢
多边形的内角和
阅读课本本课时第一段至“例1”结束,解决下列问题.
1.从多边形的一个顶点出发,可以引多少条对角线 它们将多边形分成多少个三角形 填写下表:
多边形 图形 分成三角 形的个数 边数 内角和 计算规律
三角形 1 3 180° (3-2)×180°
四边形
五边形
六边形
… … … … … …
n边形
解:
多边形 图形 分成三角 形的个数 边数 内角和 计算规律
三角形 1 3 180° (3-2)×180°
四边形 2 4 360° (4-2)×180°
五边形 3 5 540° (5-2)×180°
六边形 4 6 720° (6-2)×180°
… … … … … …
n边形 n-2 n (n-2) ×180° (n-2)×180°
·设计意图·
以表格的形式将一些简单的多边形的有关三角形、边数、内角和及计算规律列举出来,从特殊到一般找到n边形的内角和规律,培养学生的归纳能力.
2.由例题可得:如果四边形的一组对角互补,那么另一组对角 .
也互补
归纳总结 n边形的内角和等于 .
(n-2)×180°
【讨论】如图,将多边形分割成若干个三角形,请你根据图形推导出多边形的内角和.
解:(n-1)·180°-180°=(n-2)·180°.
·导学建议·
可先让学生自己想,再小组交流.教师深入参与活动,必要时给予指导.可直接引导学生用添加辅助线的方法把多边形转化为三角形,最后找学生说出探索过程,其他同学补充,并说出不同观点.
多边形的外角和
阅读课本“例2”至本课时结束,仿照“例2”的探究过程,探究n(n≥3)边形的外角和.
答:因为n边形的一个外角与它相邻的内角的和是180°,n边形的n个外角加上与它相邻的内角,所得总和是n×180°,因为n边形的内角和是(n-2)×180°,∴n边形的外角和是n×180°-(n-2)×180°=360°.
归纳总结 多边形的外角和等于 .
360°
·导学建议·
预习导学部分建议用20分钟完成,以学生自主探索为主,教师巡视,必要时给予指导.
1.六边形的内角和为 ( )
A.360° B.540° C.720° D.1080°
C
2.正十二边形的一个内角的度数为 ( )
A.30° B.150° C.360° D.1800°
B
3.正十边形的每一个外角的度数为 .
36°
1.下列度数中,不可能是某个多边形的内角和的是 ( )
A.180° B.270° C.2700° D.720°
B
方法归纳交流 根据n边形内角和是(n-2)×180°可得一个多边形的内角和一定是 的倍数.
180
2.若一个四边形四个内角的度数之比为1∶3∶4∶2,则这四个内角的度数分别是 .
36°、108°、144°、72°
3.已知一个多边形的内角和是它的外角和的2倍,求这个多边形的边数.
解:设这个多边形的边数为n,则(n-2)·`180°=2×360°,解得n=6,所以这个多边形的边数是6.
4.如图,小明沿一个五边形广场的周围按逆时针方向跑步.
(1)他每跑完一圈,身体转过的角度之和是多少
(2)在图中,你能求出∠1+∠2+∠3+∠4+∠5的度数吗
·真实情境·
《2022年版数学课程标准》中指出:情境创设的真实性.本题以生活中常见的广场跑步为背景,将多边形的外角和融入其中.
解:(1)他每跑完一圈,身体转过的角度之和是360°.
(2)∠1+∠2+∠3+∠4+∠5=360°.
方法归纳交流 多边形无论边数是多少,每个顶点处取一个外角,这些外角的和都是 .
360°
1.一个多边形每一个外角都等于18°,则这个多边形的边数为 ( )
A.10 B.12 C.16 D.20
D
2.如图,在五边形ABCDE中,若去掉一个30°的角后,得到一个六边形BCDEMN,则∠1+∠2的度数为 ( )
A.210° B.110° C.150° D.100°
A
3.一个多边形的每个内角都相等,并且它的一个外角与一个内角的比为1∶3,则这个多边形为 边形.
八
4.已知两个多边形的内角总和是1800°,并且这两个多边形的边数之比为2∶5,求这两个多边形的边数.
解:设这两个多边形的边数分别为2n,5n,则180°(2n-2)+180°(5n-2)=1800°,
解得n=2,
所以2×2=4,5×2=10.
即这两个多边形的边数分别为4,10.
5.(1)如图1,图2,试研究其中∠1、∠2与∠3、∠4之间的数量关系.
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式.
解:(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°,∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,∴∠1+∠2=360°-(∠5+∠6),
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
