第十一章 三角形 复习课 课件(共26张PPT)2023-2024学年人教版数学八年级上册
文档属性
| 名称 | 第十一章 三角形 复习课 课件(共26张PPT)2023-2024学年人教版数学八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 772.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 09:11:47 | ||
图片预览








文档简介
(共26张PPT)
八年级·数学·人教版·上册
第十一章 复习课
第十一章 复习课
1.知道三角形的高、中线及角平分线,多边形的边、角、对角线,正多边形等概念,会画三角形的中线、高、角平分线.
2.知道三角形及多边形的外角和内角的性质,并能简单应用.
◎重点:能熟练应用三角形的边、角的有关知识解决问题.
◎难点:应用三角形的边、角关系解决问题.
请回顾一下,这一章我们学习了哪些知识
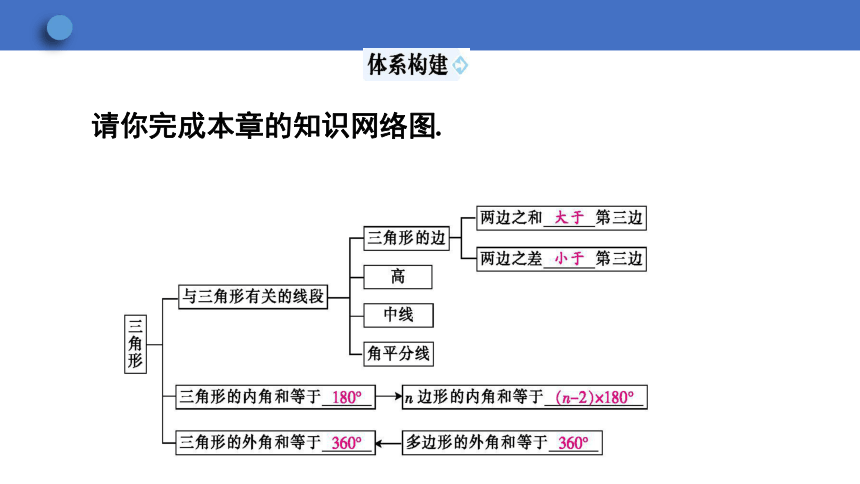
请你完成本章的知识网络图.
1.由不在 的三条线段 相接所组成的图形叫做三角形.
2.三角形两边的和 第三边,三角形两边的差
第三边.
3.三角形的内角和等于 ,三角形的一个外角等于
,三角形的一个外角
与它不相邻的任何一个内角.
首尾顺次
同一条直线上
大于
大于
小于
180°
与它不相邻的两个内角的和
4.直角三角形两锐角 ,有两个角 的三角形是直角三角形.
5.n边形从一个顶点出发可以作 条对角线,将n边形分成 个三角形,n边形共有 条对角线.
互余
互余
(n-3)
(n-2)
6.各个角都 ,各条边都 的多边形叫做正多边形.
7.n边形的内角和等于 ,任意多边形的外角和等于 .
相等
360°
相等
(n-2)×180°
·导学建议·
知识网络图可由学生自己总结,让学生理顺本章知识,形成系统.
与三角形有关的线段
1.如图, E、F、G分别是AB、BC、AC边上的中点,则S△ABC= S△FGC.
4
2.三条线段a=5,b=3,c的值为整数,若由a、b、c为边可组成三角形,则c可取的值的个数为 ( )
A.1 B.3 C.5 D.无数
C
变式演练 等腰三角形的周长为30 cm,一边长为12 cm,则底边长为 .
6 cm或12 cm
方法归纳交流 已知三角形的两边,则已知两边的 <三角形的第三边<已知两边的 .
和
差
·导学建议·
重点关注:解“变式演练”时,学生对分类讨论的思想方法能否正确运用.
三角形及多边形的内外角和
3.若正n边形的一个内角等于144°,则n的值为 ( )
A.8 B.9 C.10 D.11
C
4.已知在△ABC中,∠A=40°,∠B-∠C=40°,则∠B=
,∠C= .
50°
90°
变式演练 如果三角形的一个角等于其他两个角的差,那么这个三角形是 三角形.
直角
5.一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数是多少
解:设这个多边形的边数是n,根据题意得(n-2)×180°=2×360°+180°,解得n=7.
答:这个多边形的边数是7.
6.
如图,在△ABC中,∠A∶∠ABC∶∠ACB=3∶4∶5, BD、CE分别是边AC、AB上的高, BD、CE相交于点H,求△ABC各内角的度数及∠BHC的度数.
解:设∠A=3x,则∠ABC=4x,∠ACB=5x,所以3x+4x+5x=180°,解得x=15°,即∠A=45°,∠ABC=60°,∠ACB=75°.在Rt△ACE中,因为∠A=45°,所以∠ACE=
45°,所以∠BHC=∠BDC+∠ACE=90°+45°=135°.
方法归纳交流 在利用三角形内角和定理求角时,常通过
求解.
列方程
·导学建议·
提醒学生:“三角形内角和是180°”在题目中是隐含条件,做题时勿忽略.
三角形的稳定性
7.造房子时屋顶常用三角结构,从数学角度来看,是应用了三角形的 ,而活动挂架则用了四边形的 .
不稳定性
稳定性
(1)如图1,∠1+∠2与∠B+∠C有什么关系
(2)把图1中的△ABC沿DE折叠,得到图2,填空:∠1+∠2 ∠B+∠C(填“>”、“<”或“=”),当∠A=40°时,∠B+∠C+∠1+∠2= .
(3)图3是由图1的△ABC沿DE折叠得到的,若∠A=30°,则x+y=360-(∠B+∠C+∠1+∠2)=360- = ,猜想∠BDA+∠CEA与∠A的关系是什么,并证明你的猜想.
解:(1)相等.
(2)=,280°.
(3)300,60,∠BDA+∠CEA=2∠A,证明略.
·导学建议·
合作探究部分建议用25分钟左右的时间完成.在本节教学中,应该留给学生充分的思考、操作的时间和空间,备选问题根据学情选用.
八年级·数学·人教版·上册
第十一章 复习课
第十一章 复习课
1.知道三角形的高、中线及角平分线,多边形的边、角、对角线,正多边形等概念,会画三角形的中线、高、角平分线.
2.知道三角形及多边形的外角和内角的性质,并能简单应用.
◎重点:能熟练应用三角形的边、角的有关知识解决问题.
◎难点:应用三角形的边、角关系解决问题.
请回顾一下,这一章我们学习了哪些知识
请你完成本章的知识网络图.
1.由不在 的三条线段 相接所组成的图形叫做三角形.
2.三角形两边的和 第三边,三角形两边的差
第三边.
3.三角形的内角和等于 ,三角形的一个外角等于
,三角形的一个外角
与它不相邻的任何一个内角.
首尾顺次
同一条直线上
大于
大于
小于
180°
与它不相邻的两个内角的和
4.直角三角形两锐角 ,有两个角 的三角形是直角三角形.
5.n边形从一个顶点出发可以作 条对角线,将n边形分成 个三角形,n边形共有 条对角线.
互余
互余
(n-3)
(n-2)
6.各个角都 ,各条边都 的多边形叫做正多边形.
7.n边形的内角和等于 ,任意多边形的外角和等于 .
相等
360°
相等
(n-2)×180°
·导学建议·
知识网络图可由学生自己总结,让学生理顺本章知识,形成系统.
与三角形有关的线段
1.如图, E、F、G分别是AB、BC、AC边上的中点,则S△ABC= S△FGC.
4
2.三条线段a=5,b=3,c的值为整数,若由a、b、c为边可组成三角形,则c可取的值的个数为 ( )
A.1 B.3 C.5 D.无数
C
变式演练 等腰三角形的周长为30 cm,一边长为12 cm,则底边长为 .
6 cm或12 cm
方法归纳交流 已知三角形的两边,则已知两边的 <三角形的第三边<已知两边的 .
和
差
·导学建议·
重点关注:解“变式演练”时,学生对分类讨论的思想方法能否正确运用.
三角形及多边形的内外角和
3.若正n边形的一个内角等于144°,则n的值为 ( )
A.8 B.9 C.10 D.11
C
4.已知在△ABC中,∠A=40°,∠B-∠C=40°,则∠B=
,∠C= .
50°
90°
变式演练 如果三角形的一个角等于其他两个角的差,那么这个三角形是 三角形.
直角
5.一个多边形的内角和比它的外角和的2倍还大180°,这个多边形的边数是多少
解:设这个多边形的边数是n,根据题意得(n-2)×180°=2×360°+180°,解得n=7.
答:这个多边形的边数是7.
6.
如图,在△ABC中,∠A∶∠ABC∶∠ACB=3∶4∶5, BD、CE分别是边AC、AB上的高, BD、CE相交于点H,求△ABC各内角的度数及∠BHC的度数.
解:设∠A=3x,则∠ABC=4x,∠ACB=5x,所以3x+4x+5x=180°,解得x=15°,即∠A=45°,∠ABC=60°,∠ACB=75°.在Rt△ACE中,因为∠A=45°,所以∠ACE=
45°,所以∠BHC=∠BDC+∠ACE=90°+45°=135°.
方法归纳交流 在利用三角形内角和定理求角时,常通过
求解.
列方程
·导学建议·
提醒学生:“三角形内角和是180°”在题目中是隐含条件,做题时勿忽略.
三角形的稳定性
7.造房子时屋顶常用三角结构,从数学角度来看,是应用了三角形的 ,而活动挂架则用了四边形的 .
不稳定性
稳定性
(1)如图1,∠1+∠2与∠B+∠C有什么关系
(2)把图1中的△ABC沿DE折叠,得到图2,填空:∠1+∠2 ∠B+∠C(填“>”、“<”或“=”),当∠A=40°时,∠B+∠C+∠1+∠2= .
(3)图3是由图1的△ABC沿DE折叠得到的,若∠A=30°,则x+y=360-(∠B+∠C+∠1+∠2)=360- = ,猜想∠BDA+∠CEA与∠A的关系是什么,并证明你的猜想.
解:(1)相等.
(2)=,280°.
(3)300,60,∠BDA+∠CEA=2∠A,证明略.
·导学建议·
合作探究部分建议用25分钟左右的时间完成.在本节教学中,应该留给学生充分的思考、操作的时间和空间,备选问题根据学情选用.
