2.2.1 数轴 课件 19张PPT 2023—2024学年华东师大版数学七年级上册
文档属性
| 名称 | 2.2.1 数轴 课件 19张PPT 2023—2024学年华东师大版数学七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 50.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 10:48:17 | ||
图片预览





文档简介
(共19张PPT)
01
复习旧知
复习旧知
复习旧知
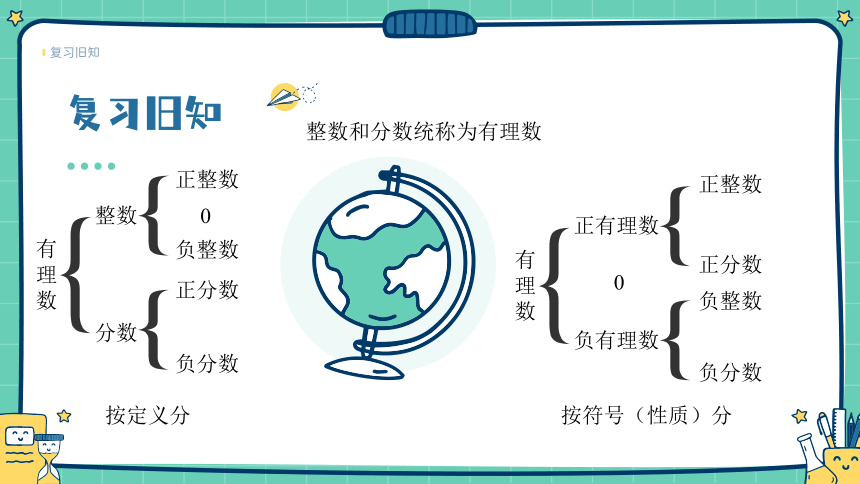
有理数
整数
分数
正整数
0
负整数
正分数
负分数
按定义分
有理数
正有理数
负有理数
0
正整数
正分数
负整数
负分数
按符号(性质)分
整数和分数统称为有理数
2.2.1 数轴
01
探究新知
探究新知
观察如图的温度计,回答下列问题:
(1)你能读出每个温度计上的温度吗?
(2)温度计刻度的基准刻度表示多少摄氏度呢?
(3)每摄氏度两条刻度线之间的距离有什么特点呢?
探究新知
画一条直线
(一般是水平直线);
任取一点作为原点,用这点表示数0;
规定原点向右为正方向,用箭头表示;
选取适当的长度作为单位长度(单位长度应统一);
在原点左右两边依次标上对应的刻度数
(一般位于直线下方)。
一画
二取
三定
四统一
五标数
探究新知
画一条直线
(一般是水平直线);
任取一点作为原点,用这点表示数0;
规定原点向右为正方向,用箭头表示;
选取适当的长度作为单位长度(单位长度应统一);
在原点左右两边依次标上对应的刻度数
(一般位于直线下方)。
一画
二取
三定
四统一
五标数
一画二取三定向,
0放中间不能忘,
线画水平两边延,
箭头指向最右边,
刻度下边数相连。
探究新知
画一条直线
(一般是水平直线);
任取一点作为原点,用这点表示数0;
规定原点向右为正方向,用箭头表示;
选取适当的长度作为单位长度(单位长度应统一);
在原点左右两边依次标上对应的刻度数
(一般位于直线下方)。
一画
二取
三定
四统一
五标数
原点
正方向
单位长度
直线
探究新知
定义:规定了原点、正方向和单位长度的直线叫做数轴。
(1)数轴是一条直线,可以向两端无限延伸。
(2)三元素:原点、正方向、单位长度,三者缺一不可。
(3)在解决具体问题时,可以灵活选取单位长度的大小。
02
想一想,练一练
想一想,练一练
例1 判断下面画的数轴是否正确,并说明理由。
-2
-1
1
2
-1
0
1
2
1
0
-1
-2
-1
0
1
2
0
-1
0
1
2
-100
0
100
200
-1
0
1
2
错
错
错
错
错
错
对
对
想一想,练一练
例2 画出数轴,并在数轴上画出表示下列各数的点:
在数轴上表示已知数
(1)先根据这个数的正负号确定它在原点的哪一边。
——正数在原点的右边,负数在原点的左边
(2)在相应的方向上确定它与原点相距几个单位长度,然后画上相应的点,在点的上边标数。
(3)任何一个有理数都可以用数轴上的一个点来表示。
数
形
想一想,练一练
例3 在下面数轴上,A、B、C、D各点分别表示什么数?
-1
0
1
2
3
4
-2
-3
-4
B
A
C
D
求数轴上已知点表示的数
(1)根据已知点是在原点的哪一边来确定它表示正数还是负数。
(2)根据该点与原点相距几个单位长度,即可知道该点表示的数。
形
数
想一想,练一练
例4 下列说法正确的是( )
A、数轴是一条带箭头的射线
B、数轴一定取向右为正方向
C、数轴是一条规定了原点、单位长度和正方向的直线
D、数轴上的原点表示有理数的起点
C
例5 数轴上表示-2的点在原点的_______侧,距原点的距离是___________,表示6的点在原点的________侧,距原点的距离是________________。
例6 离原点距离为5个单位的点表示的数是_______________。
左
右
2个单位
6个单位
5和-5
想一想,练一练
例7 数轴上一动点A先向左移动2个单位长度到达B点,再向右移动5个单位长度到达点C。若点C表示的数是1,则点A表示的数是_______。
-2
例9 小明从A地向东走了100m,然后返回向西走了30m又返回向东走了60m,问此时小明在出发点A的哪个方向?相距多远?
例8 数轴上点A和点B的距离为6,点A表示数-2,则点B表示的数为____________。
-8或4
想一想,做一做
例10 判断:
(1)数轴上的两个点可以表示同一个有理数。_______
(2)数轴上的点只能表示正数。__________
(3)两个不同的有理数,可以用数轴上同一个点表示。_______
(4)在数轴上,距离原点3个单位长度的点表示的数是3。________
×
×
×
×
例11 数轴上原点及原点左边的点表示为_______。
非正数
03
收获满满
收获满满
数轴
画法
一画:画直线
二取:取原点
三定:定正方向
四统一:统一单位长度
五标数:标上对应刻度
定义
规定了原点、正方向和单位长度的直线,叫做数轴。
应用
用数轴上的点表示给定的有理数
根据数轴上的点读出有理数
数形结合解决问题
THANKS
感谢观看
教师:周婷
01
复习旧知
复习旧知
复习旧知
有理数
整数
分数
正整数
0
负整数
正分数
负分数
按定义分
有理数
正有理数
负有理数
0
正整数
正分数
负整数
负分数
按符号(性质)分
整数和分数统称为有理数
2.2.1 数轴
01
探究新知
探究新知
观察如图的温度计,回答下列问题:
(1)你能读出每个温度计上的温度吗?
(2)温度计刻度的基准刻度表示多少摄氏度呢?
(3)每摄氏度两条刻度线之间的距离有什么特点呢?
探究新知
画一条直线
(一般是水平直线);
任取一点作为原点,用这点表示数0;
规定原点向右为正方向,用箭头表示;
选取适当的长度作为单位长度(单位长度应统一);
在原点左右两边依次标上对应的刻度数
(一般位于直线下方)。
一画
二取
三定
四统一
五标数
探究新知
画一条直线
(一般是水平直线);
任取一点作为原点,用这点表示数0;
规定原点向右为正方向,用箭头表示;
选取适当的长度作为单位长度(单位长度应统一);
在原点左右两边依次标上对应的刻度数
(一般位于直线下方)。
一画
二取
三定
四统一
五标数
一画二取三定向,
0放中间不能忘,
线画水平两边延,
箭头指向最右边,
刻度下边数相连。
探究新知
画一条直线
(一般是水平直线);
任取一点作为原点,用这点表示数0;
规定原点向右为正方向,用箭头表示;
选取适当的长度作为单位长度(单位长度应统一);
在原点左右两边依次标上对应的刻度数
(一般位于直线下方)。
一画
二取
三定
四统一
五标数
原点
正方向
单位长度
直线
探究新知
定义:规定了原点、正方向和单位长度的直线叫做数轴。
(1)数轴是一条直线,可以向两端无限延伸。
(2)三元素:原点、正方向、单位长度,三者缺一不可。
(3)在解决具体问题时,可以灵活选取单位长度的大小。
02
想一想,练一练
想一想,练一练
例1 判断下面画的数轴是否正确,并说明理由。
-2
-1
1
2
-1
0
1
2
1
0
-1
-2
-1
0
1
2
0
-1
0
1
2
-100
0
100
200
-1
0
1
2
错
错
错
错
错
错
对
对
想一想,练一练
例2 画出数轴,并在数轴上画出表示下列各数的点:
在数轴上表示已知数
(1)先根据这个数的正负号确定它在原点的哪一边。
——正数在原点的右边,负数在原点的左边
(2)在相应的方向上确定它与原点相距几个单位长度,然后画上相应的点,在点的上边标数。
(3)任何一个有理数都可以用数轴上的一个点来表示。
数
形
想一想,练一练
例3 在下面数轴上,A、B、C、D各点分别表示什么数?
-1
0
1
2
3
4
-2
-3
-4
B
A
C
D
求数轴上已知点表示的数
(1)根据已知点是在原点的哪一边来确定它表示正数还是负数。
(2)根据该点与原点相距几个单位长度,即可知道该点表示的数。
形
数
想一想,练一练
例4 下列说法正确的是( )
A、数轴是一条带箭头的射线
B、数轴一定取向右为正方向
C、数轴是一条规定了原点、单位长度和正方向的直线
D、数轴上的原点表示有理数的起点
C
例5 数轴上表示-2的点在原点的_______侧,距原点的距离是___________,表示6的点在原点的________侧,距原点的距离是________________。
例6 离原点距离为5个单位的点表示的数是_______________。
左
右
2个单位
6个单位
5和-5
想一想,练一练
例7 数轴上一动点A先向左移动2个单位长度到达B点,再向右移动5个单位长度到达点C。若点C表示的数是1,则点A表示的数是_______。
-2
例9 小明从A地向东走了100m,然后返回向西走了30m又返回向东走了60m,问此时小明在出发点A的哪个方向?相距多远?
例8 数轴上点A和点B的距离为6,点A表示数-2,则点B表示的数为____________。
-8或4
想一想,做一做
例10 判断:
(1)数轴上的两个点可以表示同一个有理数。_______
(2)数轴上的点只能表示正数。__________
(3)两个不同的有理数,可以用数轴上同一个点表示。_______
(4)在数轴上,距离原点3个单位长度的点表示的数是3。________
×
×
×
×
例11 数轴上原点及原点左边的点表示为_______。
非正数
03
收获满满
收获满满
数轴
画法
一画:画直线
二取:取原点
三定:定正方向
四统一:统一单位长度
五标数:标上对应刻度
定义
规定了原点、正方向和单位长度的直线,叫做数轴。
应用
用数轴上的点表示给定的有理数
根据数轴上的点读出有理数
数形结合解决问题
THANKS
感谢观看
教师:周婷
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
