3.3.2抛物线的简单几何性质(第一课时) 课件(共33张PPT)
文档属性
| 名称 | 3.3.2抛物线的简单几何性质(第一课时) 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1016.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-12 22:54:51 | ||
图片预览








文档简介
(共33张PPT)
3.3.2 抛物线的简单几何性质
(第一课时)
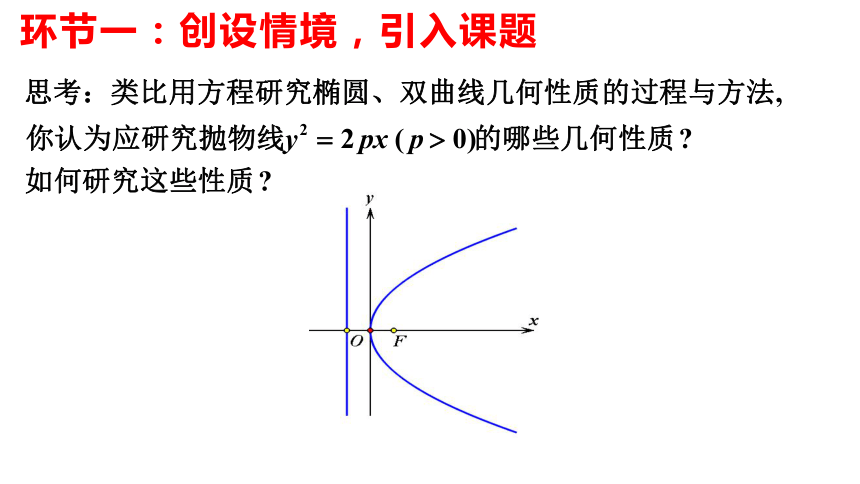
环节一:创设情境,引入课题
1. 范围
1.几何角度
2.代数角度
2. 对称性
1.几何角度
2.代数角度
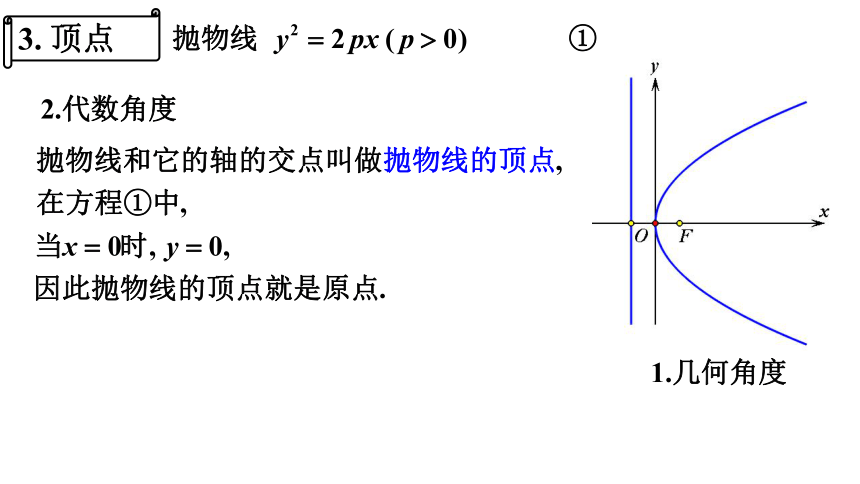
3. 顶点
1.几何角度
2.代数角度
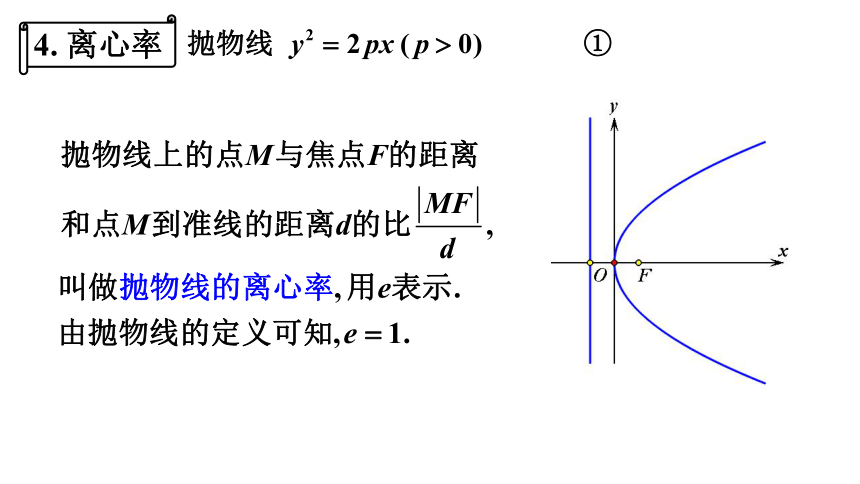
4. 离心率
(1)范围:
(2)对称性:关于x轴对称
抛物线的对称轴叫做抛物线的轴.
(3)顶点(抛物线与轴的交点):
(4)离心率:
(5)p对抛物线的影响:p越大,开口越大
抛物线的简单几何性质
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
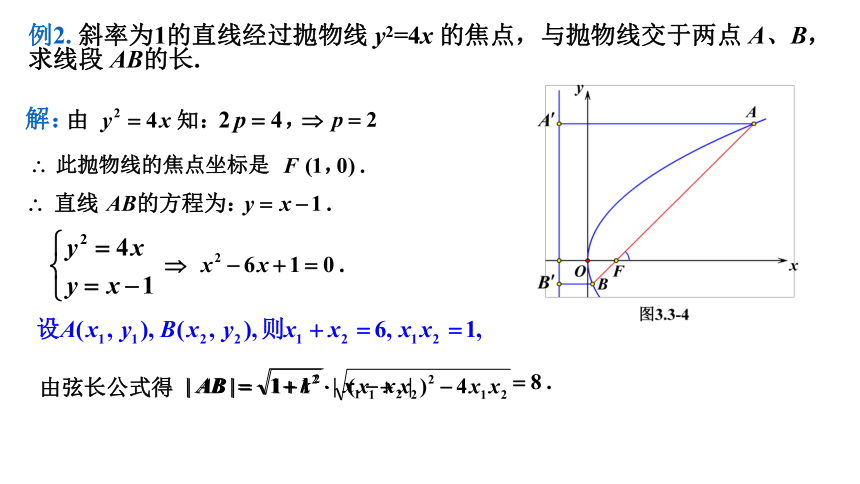
解法1(代数法): 由题意知抛物线的焦点 F(1 , 0)
联立得:
例2. 斜率为1的直线经过抛物线 y2=4x 的焦点,与抛物线交于两点 A、B,求线段 AB的长.
解:
下面介绍另外一种方法——数形结合的方法.
A
B
F
O
x
y
焦点弦
过抛物线的焦点且与抛物线相交的直线,
被抛物线截取的线段叫抛物线的焦点弦.
A′
B′
A
B
O
x
y
F
抛物线 的焦点弦长公式:
设
则
焦点弦中与对称轴垂直的弦叫做抛物线的通径,
长度为2p.这是标准方程中2p的几何意义.
过焦点而垂直于对称轴的弦AB,称为抛物线的通径.
|AB|=2p
5.通径
A
B
y2=2px
2p
x
l
F
y
O
抛物线方程中2p的几何意义
问题3 双曲线的开口大小由离心率来衡量,那么抛物线的开口大小怎样确定呢?
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
2p越大,抛物线张口越大
(1) 抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
(2) 抛物线只有一条对称轴,没有对称中心;
(3) 抛物线只有一个顶点,一个焦点,一条准线;
(4) 抛物线的离心率e是确定的为1,
(5) 抛物线的通径为2p, 2p越大,抛物线的张口越大.
归纳
抛物线的焦点弦
抛物线的焦点弦长
抛物线的焦点弦长
小结:圆锥曲线的弦长
法一:求交点(联立方程组求交点坐标,用两点间的距离公式)
法二:弦长公式(适用于斜率为k的直线和曲线C相交所得弦长)
法四:圆的弦长
法三:抛物线的弦长
教材练习(第136页)
2.在同一坐标系中画出下列抛物线,观察它们开口的大小,并说明抛物线开口大小与方程中的x系数的关系:
抛物线如图,x的系数的绝对值越大,抛物线的开口越大.
解:
由定义得,
x
y
F
A
B
K
O
|AB|= |AF|+|BF|
思考:抛物线中过焦点的弦有最小值吗?如果有,在何处取得?
通径是抛物线中过焦点的最短弦长度为2p.
抛物线的焦半径和焦点弦公式(一)
抛物线的焦半径和焦点弦公式(二)
A
B
O
F
K
N
M
H
x
y
在抛物线的所有焦点弦中,通径最短
A
B
O
F
K
N
M
H
x
y
探究2:抛物线的焦半径
上-下+
例2.在抛物线 y2=8x 上求一点P,使P到焦点F 的距离与到 Q(4 ,1)的距离的和最小,并求最小值。
解:
K
x
y
Q
2
F
O
4
P
思考:
当| |PF|-|PQ| |为最大时,点P的坐标是_______.
课堂小结:以y2=2px(p>0)为例
x
y
3.3.2 抛物线的简单几何性质
(第一课时)
环节一:创设情境,引入课题
1. 范围
1.几何角度
2.代数角度
2. 对称性
1.几何角度
2.代数角度
3. 顶点
1.几何角度
2.代数角度
4. 离心率
(1)范围:
(2)对称性:关于x轴对称
抛物线的对称轴叫做抛物线的轴.
(3)顶点(抛物线与轴的交点):
(4)离心率:
(5)p对抛物线的影响:p越大,开口越大
抛物线的简单几何性质
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
例2 斜率为1的直线l经过抛物线y2=4x的焦点F,且与抛物线相交于A,B两点,求线段AB的长.
l
F
A
A1
x
y
B
B1
解法1(代数法): 由题意知抛物线的焦点 F(1 , 0)
联立得:
例2. 斜率为1的直线经过抛物线 y2=4x 的焦点,与抛物线交于两点 A、B,求线段 AB的长.
解:
下面介绍另外一种方法——数形结合的方法.
A
B
F
O
x
y
焦点弦
过抛物线的焦点且与抛物线相交的直线,
被抛物线截取的线段叫抛物线的焦点弦.
A′
B′
A
B
O
x
y
F
抛物线 的焦点弦长公式:
设
则
焦点弦中与对称轴垂直的弦叫做抛物线的通径,
长度为2p.这是标准方程中2p的几何意义.
过焦点而垂直于对称轴的弦AB,称为抛物线的通径.
|AB|=2p
5.通径
A
B
y2=2px
2p
x
l
F
y
O
抛物线方程中2p的几何意义
问题3 双曲线的开口大小由离心率来衡量,那么抛物线的开口大小怎样确定呢?
利用抛物线的顶点、通径的两个端点可较准确画出反映抛物线基本特征的草图.
2p越大,抛物线张口越大
(1) 抛物线只位于半个坐标平面内,虽然它也可以无限延伸,但没有渐近线;
(2) 抛物线只有一条对称轴,没有对称中心;
(3) 抛物线只有一个顶点,一个焦点,一条准线;
(4) 抛物线的离心率e是确定的为1,
(5) 抛物线的通径为2p, 2p越大,抛物线的张口越大.
归纳
抛物线的焦点弦
抛物线的焦点弦长
抛物线的焦点弦长
小结:圆锥曲线的弦长
法一:求交点(联立方程组求交点坐标,用两点间的距离公式)
法二:弦长公式(适用于斜率为k的直线和曲线C相交所得弦长)
法四:圆的弦长
法三:抛物线的弦长
教材练习(第136页)
2.在同一坐标系中画出下列抛物线,观察它们开口的大小,并说明抛物线开口大小与方程中的x系数的关系:
抛物线如图,x的系数的绝对值越大,抛物线的开口越大.
解:
由定义得,
x
y
F
A
B
K
O
|AB|= |AF|+|BF|
思考:抛物线中过焦点的弦有最小值吗?如果有,在何处取得?
通径是抛物线中过焦点的最短弦长度为2p.
抛物线的焦半径和焦点弦公式(一)
抛物线的焦半径和焦点弦公式(二)
A
B
O
F
K
N
M
H
x
y
在抛物线的所有焦点弦中,通径最短
A
B
O
F
K
N
M
H
x
y
探究2:抛物线的焦半径
上-下+
例2.在抛物线 y2=8x 上求一点P,使P到焦点F 的距离与到 Q(4 ,1)的距离的和最小,并求最小值。
解:
K
x
y
Q
2
F
O
4
P
思考:
当| |PF|-|PQ| |为最大时,点P的坐标是_______.
课堂小结:以y2=2px(p>0)为例
x
y
