24.2点和圆、直线和圆的位置关系同步练习 人教版数学九年级上册(无答案)
文档属性
| 名称 | 24.2点和圆、直线和圆的位置关系同步练习 人教版数学九年级上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 246.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 11:34:54 | ||
图片预览

文档简介
24.2点和圆、直线和圆的位置关系
一、单选题
1.如图,切于,点从出发,以每秒的速度沿方向运动,运动2秒时,运动4秒时长是( )
A. B. C. D.
2.对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )
A.∠α=60°,∠α的补角∠β=120°,∠β>∠α B.∠α=90°,∠α的补角∠β=90°,∠β=∠α
C.∠α=100°,∠α的补角∠β=80°,∠β<∠α D.两个角互为邻补角
3.如图,是的直径,过点作的切线,连接,与交于点,点是上一点,连接,.若,则的度数为( )
A.30° B.40° C.50° D.60°
4.如图,AB是⊙O的直径,MT切⊙O于点T.若∠MTA=50°,则∠BOT的度数为( )
A.50° B.60° C.80° D.100°
5.已知平面内有与直线,的半径为,点O到直线的距离为,则直线与的位置关系是( )
A.相切 B.相交 C.相离 D.不能判断
6.已知⊙O半径为5,线段OP=6,A为OP的中点,点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
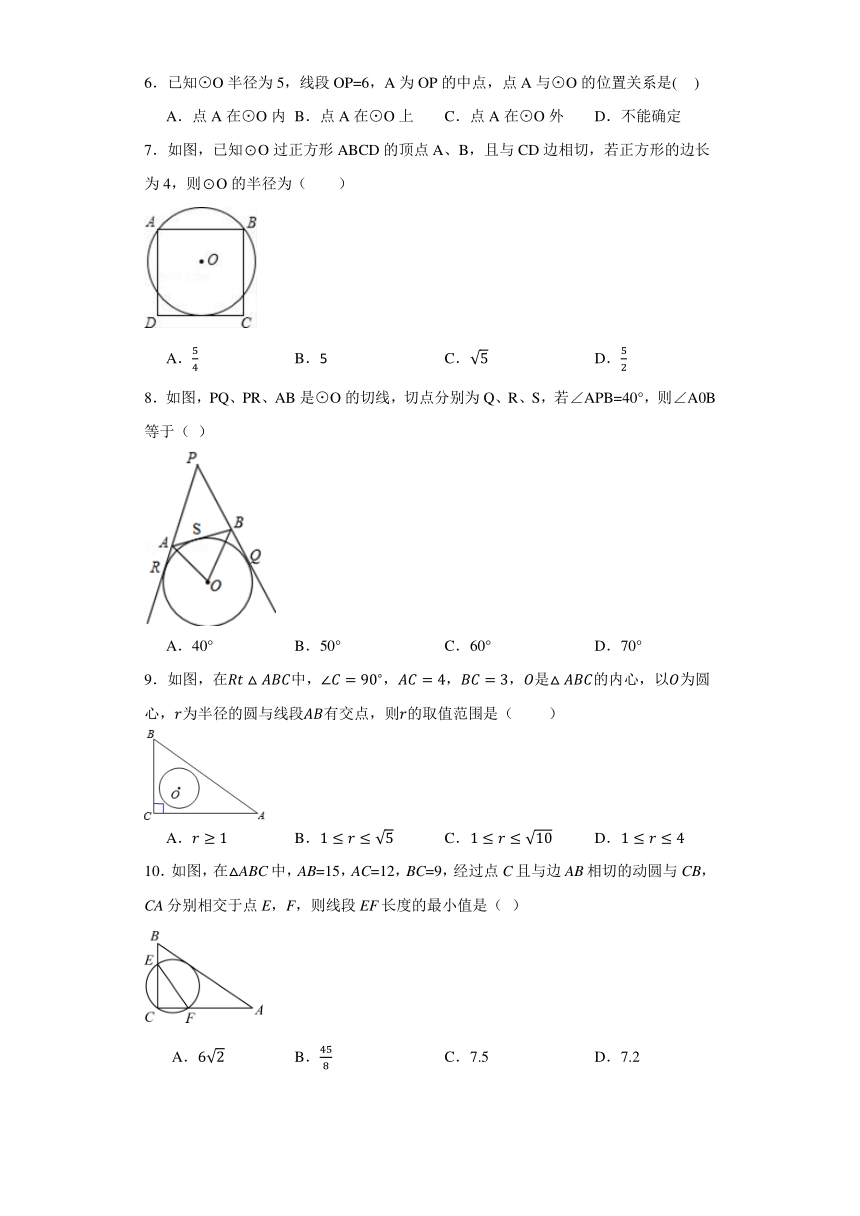
7.如图,已知⊙O过正方形ABCD的顶点A、B,且与CD边相切,若正方形的边长为4,则⊙O的半径为( )
A. B.5 C. D.
8.如图,PQ、PR、AB是⊙O的切线,切点分别为Q、R、S,若∠APB=40°,则∠A0B等于( )
A.40° B.50° C.60° D.70°
9.如图,在中,,,,是的内心,以为圆心,为半径的圆与线段有交点,则的取值范围是( )
A. B. C. D.
10.如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是( )
A. B. C.7.5 D.7.2
二、填空题
11.如图,已知在中,,,,点是的内心.
(1)点到边的距离为 ;
(2)是的外心,连接,则的长为 .
12.如图,正方形ABCD的边长为4,E是AD的中点,点P是边AB上的一个动点,连接PE,以P为圆心,PE的长为半径作.当与正方形ABCD的边相切时,则AP的长为 .
13.如图是一块直角三角形木料,,,,木工师傅要从中裁下一块圆形用料,则可裁圆形木料的最大半径为 .
14.如图,⊙O的半径为4 cm,BC是直径,若AB=10 cm,则AC= cm时,AC是⊙O的切线.
15.如图所示,在三角形中,,两直角边,,三角形内有一点,它到各边的距离相等,则这个距离是 .
三、解答题
16.如图,在中,直径垂直于不过圆心的弦,垂足为点,连接,,点在上,且.过点作的切线交的延长线于点,点为上一动点,设线段的长为.
(1)求证:;
(2)求证:;
(3)设半径为,若点为中点,求的取值范围.
17.如图,△ABC内接于⊙O,OC⊥AB于点E,点D在OC的延长线上,且∠B=∠D=30°.(1)求证:AD是⊙O的切线;(2)若,求⊙O的半径.
18.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
19.(1)如图1,在四边形ABCD是矩形,点E是AD的中点,求证:EB=EC.
(2)如图2,AB与相切于C,,⊙O的半径为6,AB=16,求OA的长.
20.如图,点O在∠ABC的边BC上,以OB为半径作⊙O,∠ABC的平分线BM交⊙O于点D,过点D作DE⊥BA于点E.
(1)尺规作图(不写作法,保留作图痕迹),补全图形;
(2)判断⊙O与DE交点的个数,并说明理由.
21.如图,已知一次函数的图象分别与y轴、x轴交于点A、B.设点M在射线上,将点M绕点A按逆时针方向旋转90°到点N,以点N为圆心,NA的长为半径作.
(1)当与x轴相切时,求点M的坐标;
(2)在(1)的条件下,设直线与x轴交于点C,与的另一个交点为D,连接交x轴于点E,直线m:过点N,且分别与y轴、直线l交于点P、Q,若满足与相似,试求直线m的解析式.
一、单选题
1.如图,切于,点从出发,以每秒的速度沿方向运动,运动2秒时,运动4秒时长是( )
A. B. C. D.
2.对假命题“任何一个角的补角都不小于这个角”举反例,正确的反例是( )
A.∠α=60°,∠α的补角∠β=120°,∠β>∠α B.∠α=90°,∠α的补角∠β=90°,∠β=∠α
C.∠α=100°,∠α的补角∠β=80°,∠β<∠α D.两个角互为邻补角
3.如图,是的直径,过点作的切线,连接,与交于点,点是上一点,连接,.若,则的度数为( )
A.30° B.40° C.50° D.60°
4.如图,AB是⊙O的直径,MT切⊙O于点T.若∠MTA=50°,则∠BOT的度数为( )
A.50° B.60° C.80° D.100°
5.已知平面内有与直线,的半径为,点O到直线的距离为,则直线与的位置关系是( )
A.相切 B.相交 C.相离 D.不能判断
6.已知⊙O半径为5,线段OP=6,A为OP的中点,点A与⊙O的位置关系是( )
A.点A在⊙O内 B.点A在⊙O上 C.点A在⊙O外 D.不能确定
7.如图,已知⊙O过正方形ABCD的顶点A、B,且与CD边相切,若正方形的边长为4,则⊙O的半径为( )
A. B.5 C. D.
8.如图,PQ、PR、AB是⊙O的切线,切点分别为Q、R、S,若∠APB=40°,则∠A0B等于( )
A.40° B.50° C.60° D.70°
9.如图,在中,,,,是的内心,以为圆心,为半径的圆与线段有交点,则的取值范围是( )
A. B. C. D.
10.如图,在△ABC中,AB=15,AC=12,BC=9,经过点C且与边AB相切的动圆与CB,CA分别相交于点E,F,则线段EF长度的最小值是( )
A. B. C.7.5 D.7.2
二、填空题
11.如图,已知在中,,,,点是的内心.
(1)点到边的距离为 ;
(2)是的外心,连接,则的长为 .
12.如图,正方形ABCD的边长为4,E是AD的中点,点P是边AB上的一个动点,连接PE,以P为圆心,PE的长为半径作.当与正方形ABCD的边相切时,则AP的长为 .
13.如图是一块直角三角形木料,,,,木工师傅要从中裁下一块圆形用料,则可裁圆形木料的最大半径为 .
14.如图,⊙O的半径为4 cm,BC是直径,若AB=10 cm,则AC= cm时,AC是⊙O的切线.
15.如图所示,在三角形中,,两直角边,,三角形内有一点,它到各边的距离相等,则这个距离是 .
三、解答题
16.如图,在中,直径垂直于不过圆心的弦,垂足为点,连接,,点在上,且.过点作的切线交的延长线于点,点为上一动点,设线段的长为.
(1)求证:;
(2)求证:;
(3)设半径为,若点为中点,求的取值范围.
17.如图,△ABC内接于⊙O,OC⊥AB于点E,点D在OC的延长线上,且∠B=∠D=30°.(1)求证:AD是⊙O的切线;(2)若,求⊙O的半径.
18.如图,A,P,B,C是半径为8的⊙O上的四点,且满足∠BAC=∠APC=60°,
(1)求证:△ABC是等边三角形;
(2)求圆心O到BC的距离OD.
19.(1)如图1,在四边形ABCD是矩形,点E是AD的中点,求证:EB=EC.
(2)如图2,AB与相切于C,,⊙O的半径为6,AB=16,求OA的长.
20.如图,点O在∠ABC的边BC上,以OB为半径作⊙O,∠ABC的平分线BM交⊙O于点D,过点D作DE⊥BA于点E.
(1)尺规作图(不写作法,保留作图痕迹),补全图形;
(2)判断⊙O与DE交点的个数,并说明理由.
21.如图,已知一次函数的图象分别与y轴、x轴交于点A、B.设点M在射线上,将点M绕点A按逆时针方向旋转90°到点N,以点N为圆心,NA的长为半径作.
(1)当与x轴相切时,求点M的坐标;
(2)在(1)的条件下,设直线与x轴交于点C,与的另一个交点为D,连接交x轴于点E,直线m:过点N,且分别与y轴、直线l交于点P、Q,若满足与相似,试求直线m的解析式.
同课章节目录
