24.4弧长和扇形面积同步练习 人教版数学九年级上册(无答案)
文档属性
| 名称 | 24.4弧长和扇形面积同步练习 人教版数学九年级上册(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 211.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 11:23:16 | ||
图片预览


文档简介
24.4弧长和扇形面积
一、单选题
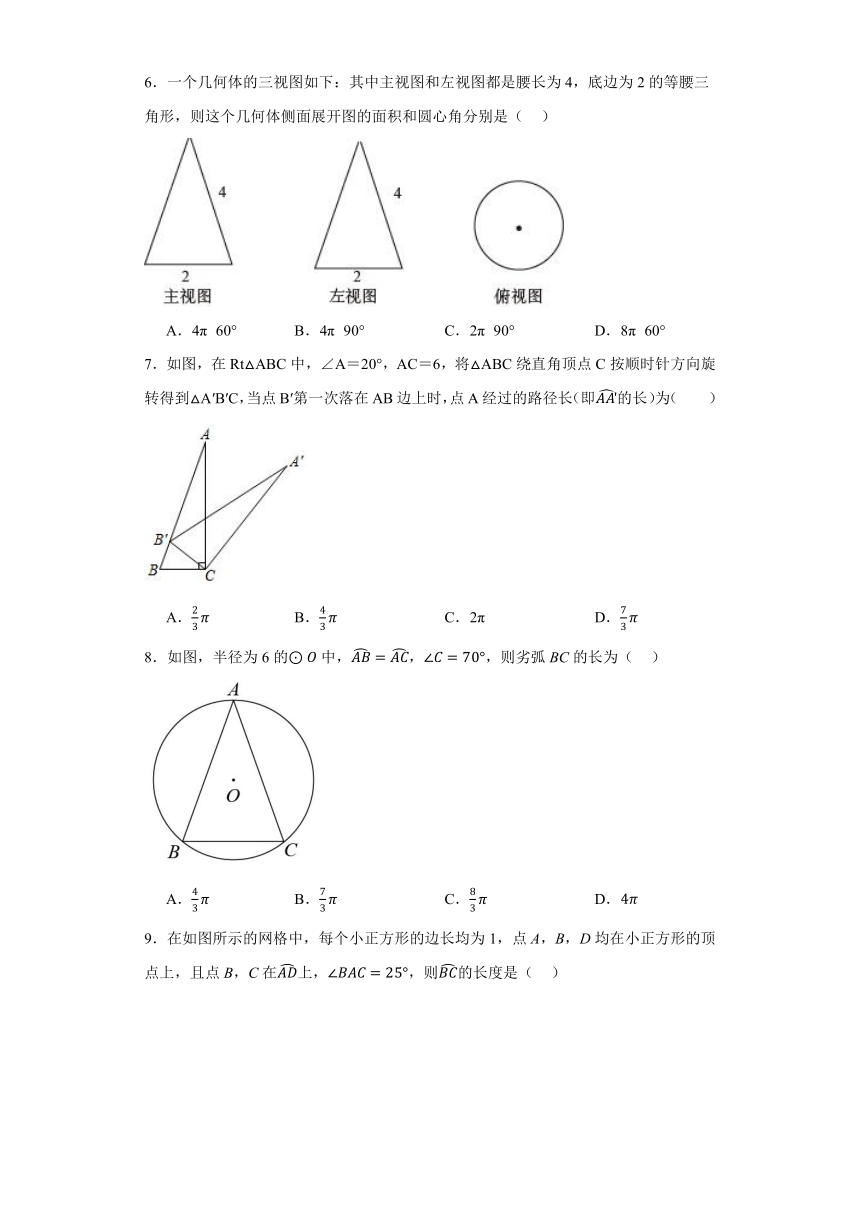
1.如图,ABCDEF为⊙O的内接正六边形,AB=a,则图中阴影部分的面积是( )
A. B. C. D.
2.如图,圆柱的底面周长为16,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S,则移动的最短距离为( )
A.10 B.12 C.14 D.20
3.如图,是的切线,B为切点,与交于点C,以点A为圆心、以的长为半径,作,分别交于点E、F.若,,则图中阴影部分的面积为( )
A. B. C. D.
4.已知圆心角为的扇形的弧长为,该扇形的面积为( )
A. B. C. D.
5.圆锥的母线长为8cm,底面半径为6cm,则圆锥的侧面积是 ( )
A.96πcm2 B.60πcm2 C.48πcm2 D.24πcm2
6.一个几何体的三视图如下:其中主视图和左视图都是腰长为4,底边为2的等腰三角形,则这个几何体侧面展开图的面积和圆心角分别是( )
A.4π 60° B.4π 90° C.2π 90° D.8π 60°
7.如图,在Rt△ABC中,∠A=20°,AC=6,将△ABC绕直角顶点C按顺时针方向旋转得到△A′B′C,当点B′第一次落在AB边上时,点A经过的路径长(即的长)为( )
A. B. C.2π D.
8.如图,半径为6的中,,,则劣弧BC的长为( )
A. B. C. D.
9.在如图所示的网格中,每个小正方形的边长均为1,点A,B,D均在小正方形的顶点上,且点B,C在上,,则的长度是( )
A. B. C. D.
10.已知圆锥的底面半径为4,母线长为6,则它的侧面展开图的面积是( )
A.24 B.48 C.12 D.24
二、填空题
11.如图在Rt△AOB中,∠ABO=90°,将Rt△AOB绕点O顺时针旋转120°得Rt△COD、已知AB=1,那么图中阴影部分的面积为 (结果保留π)
12.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为 .
13.如图,边长为1的正方形绕点逆时针旋转后得到正方形,边与交于点,其中点的运动路径为弧,则图中阴影部分的面积是 .
14.已知扇形的圆心角为120°,弧长为12πcm,则扇形的半径为 cm.
15.如图是圆锥及其侧面展开图.若,,则圆锥展开图中为 .
三、解答题
16.如图,四边形是正方形,曲线…叫做“正方形的渐开线”,其中,…的圆心依次按A,B,C,D循环.当时,曲线的长度是多少?
17.已知:如图,AB为⊙O的直径,C,D是⊙O直径AB异侧的两点,AC=DC,过点C与⊙O相切的直线CF交弦DB的延长线于点E.
(1)试判断直线DE与CF的位置关系,并说明理由;
(2)若∠A=30°,AB=4,求的长.
18.如图,四边形内接于,是的直径,平分,交于点.
(1)判断与的位置关系,并说明理由;
(2)当,时,求劣弧的长度.
19.【综合与实践】
【问题情境】在学习了数学活动《车轮做成圆形的数学道理》后,数学学习小组的同学们利用计算机软件继续模拟并探讨各种不同类型的图形的滚动问题.
【实践探究】同学们首先选择了以下四种正多边形沿水平地面的滚动,研究了以一个顶点为支点完成一次完整旋转的过程.例如,在图一中,等边三角形围绕顶点,中心从顺时针旋转到再到的过程.我们定义这个旋转过程为正多边形绕一个顶点的一次旋转.
(1)我们学习了图二中正方形绕一个顶点的一次旋转角度为,即是正方形的中心角度数,也是外角度数.那么等边三角形绕一个顶点的一次旋转角度为______;正五边形绕一个顶点的一次旋转角度为______;正边形绕一个顶点的一次旋转角度为______;
【深入探究】同学们继续模拟并探究,如果不是沿着水平地面滚动又会是怎样的情况?
(2)如图五,半径为2的正五边形在另一个相同半径的正五边形的边上顺时针滚动,初始时正五边形绕顶点的一次旋转中,中心旋转到,则这一次旋转的旋转角度是多大?沿正五边形滚动一周后回到原来的位置,中心的运动路径长为多少?
【问题解决】如果将正多边形变化为其他图形又会是怎样的情况呢?
(3)如图六,点为上的点,,,由弦及弧组成的类似扇形的图形沿着水平地面顺时针滚动一周,直接写出圆心的运动路径的长.
20.如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1请在图中画出Rt△A1B1C1;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,请在图中画出Rt△A2B2C2,并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长.
21.如图,在中,,以为直径的与交于点,连接.
(1)用无刻度的直尺和圆规作出劣弧的中点.(不写作法,保留作图痕迹),连接交于点,并证明:;
(2)若的半径等于,且与相切于点,求劣弧的长度和阴影部分的面积(结果保留).
一、单选题
1.如图,ABCDEF为⊙O的内接正六边形,AB=a,则图中阴影部分的面积是( )
A. B. C. D.
2.如图,圆柱的底面周长为16,BC=12,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S,则移动的最短距离为( )
A.10 B.12 C.14 D.20
3.如图,是的切线,B为切点,与交于点C,以点A为圆心、以的长为半径,作,分别交于点E、F.若,,则图中阴影部分的面积为( )
A. B. C. D.
4.已知圆心角为的扇形的弧长为,该扇形的面积为( )
A. B. C. D.
5.圆锥的母线长为8cm,底面半径为6cm,则圆锥的侧面积是 ( )
A.96πcm2 B.60πcm2 C.48πcm2 D.24πcm2
6.一个几何体的三视图如下:其中主视图和左视图都是腰长为4,底边为2的等腰三角形,则这个几何体侧面展开图的面积和圆心角分别是( )
A.4π 60° B.4π 90° C.2π 90° D.8π 60°
7.如图,在Rt△ABC中,∠A=20°,AC=6,将△ABC绕直角顶点C按顺时针方向旋转得到△A′B′C,当点B′第一次落在AB边上时,点A经过的路径长(即的长)为( )
A. B. C.2π D.
8.如图,半径为6的中,,,则劣弧BC的长为( )
A. B. C. D.
9.在如图所示的网格中,每个小正方形的边长均为1,点A,B,D均在小正方形的顶点上,且点B,C在上,,则的长度是( )
A. B. C. D.
10.已知圆锥的底面半径为4,母线长为6,则它的侧面展开图的面积是( )
A.24 B.48 C.12 D.24
二、填空题
11.如图在Rt△AOB中,∠ABO=90°,将Rt△AOB绕点O顺时针旋转120°得Rt△COD、已知AB=1,那么图中阴影部分的面积为 (结果保留π)
12.若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为 .
13.如图,边长为1的正方形绕点逆时针旋转后得到正方形,边与交于点,其中点的运动路径为弧,则图中阴影部分的面积是 .
14.已知扇形的圆心角为120°,弧长为12πcm,则扇形的半径为 cm.
15.如图是圆锥及其侧面展开图.若,,则圆锥展开图中为 .
三、解答题
16.如图,四边形是正方形,曲线…叫做“正方形的渐开线”,其中,…的圆心依次按A,B,C,D循环.当时,曲线的长度是多少?
17.已知:如图,AB为⊙O的直径,C,D是⊙O直径AB异侧的两点,AC=DC,过点C与⊙O相切的直线CF交弦DB的延长线于点E.
(1)试判断直线DE与CF的位置关系,并说明理由;
(2)若∠A=30°,AB=4,求的长.
18.如图,四边形内接于,是的直径,平分,交于点.
(1)判断与的位置关系,并说明理由;
(2)当,时,求劣弧的长度.
19.【综合与实践】
【问题情境】在学习了数学活动《车轮做成圆形的数学道理》后,数学学习小组的同学们利用计算机软件继续模拟并探讨各种不同类型的图形的滚动问题.
【实践探究】同学们首先选择了以下四种正多边形沿水平地面的滚动,研究了以一个顶点为支点完成一次完整旋转的过程.例如,在图一中,等边三角形围绕顶点,中心从顺时针旋转到再到的过程.我们定义这个旋转过程为正多边形绕一个顶点的一次旋转.
(1)我们学习了图二中正方形绕一个顶点的一次旋转角度为,即是正方形的中心角度数,也是外角度数.那么等边三角形绕一个顶点的一次旋转角度为______;正五边形绕一个顶点的一次旋转角度为______;正边形绕一个顶点的一次旋转角度为______;
【深入探究】同学们继续模拟并探究,如果不是沿着水平地面滚动又会是怎样的情况?
(2)如图五,半径为2的正五边形在另一个相同半径的正五边形的边上顺时针滚动,初始时正五边形绕顶点的一次旋转中,中心旋转到,则这一次旋转的旋转角度是多大?沿正五边形滚动一周后回到原来的位置,中心的运动路径长为多少?
【问题解决】如果将正多边形变化为其他图形又会是怎样的情况呢?
(3)如图六,点为上的点,,,由弦及弧组成的类似扇形的图形沿着水平地面顺时针滚动一周,直接写出圆心的运动路径的长.
20.如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1请在图中画出Rt△A1B1C1;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,请在图中画出Rt△A2B2C2,并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长.
21.如图,在中,,以为直径的与交于点,连接.
(1)用无刻度的直尺和圆规作出劣弧的中点.(不写作法,保留作图痕迹),连接交于点,并证明:;
(2)若的半径等于,且与相切于点,求劣弧的长度和阴影部分的面积(结果保留).
同课章节目录
