24.2.2直线和圆的位置关系同步练习 人教版数学九年级上册(无答案)
文档属性
| 名称 | 24.2.2直线和圆的位置关系同步练习 人教版数学九年级上册(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-12-13 11:38:33 | ||
图片预览

文档简介
24.2.2直线和圆的位置关系
一、单选题
1..已知⊙O1 的半径 r 为 4cm,⊙O2 的半径 R 为 5cm,两圆的圆心距 O1O2 为 6cm,则这两圆的位置关系是( )
A.相交 B.内含 C.内切 D.外切
2.如图所示,在中,,截的三边所得的弦长相等,则( )
A. B. C. D.
3.在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点.对于一条直线,当它与一个圆的公共点都是整点时,我们把这条直线称为这个圆的“整点直线”.已知⊙O是以原点为圆心,半径为 圆,则⊙O的“整点直线”共有( )条
A.7 B.8 C.9 D.10
4.在下列说法中:①三角形的外心是三角形三边垂直平分线的交点;②若两条弧的度数相等,则它们是等弧;③直径是圆中最长的弦;④如果两条弦相等,那么这两条弦所对的圆心角相等;⑤圆的切线垂直于半径;其中说法正确的个数是( )
A.2 B.3 C.4 D.5
5.两圆的半径分别为R和r,圆心距为1,且R、r分别是方程的两个根,则两圆的位置关系是( )
A.相交 B.外切 C.内切 D.外离
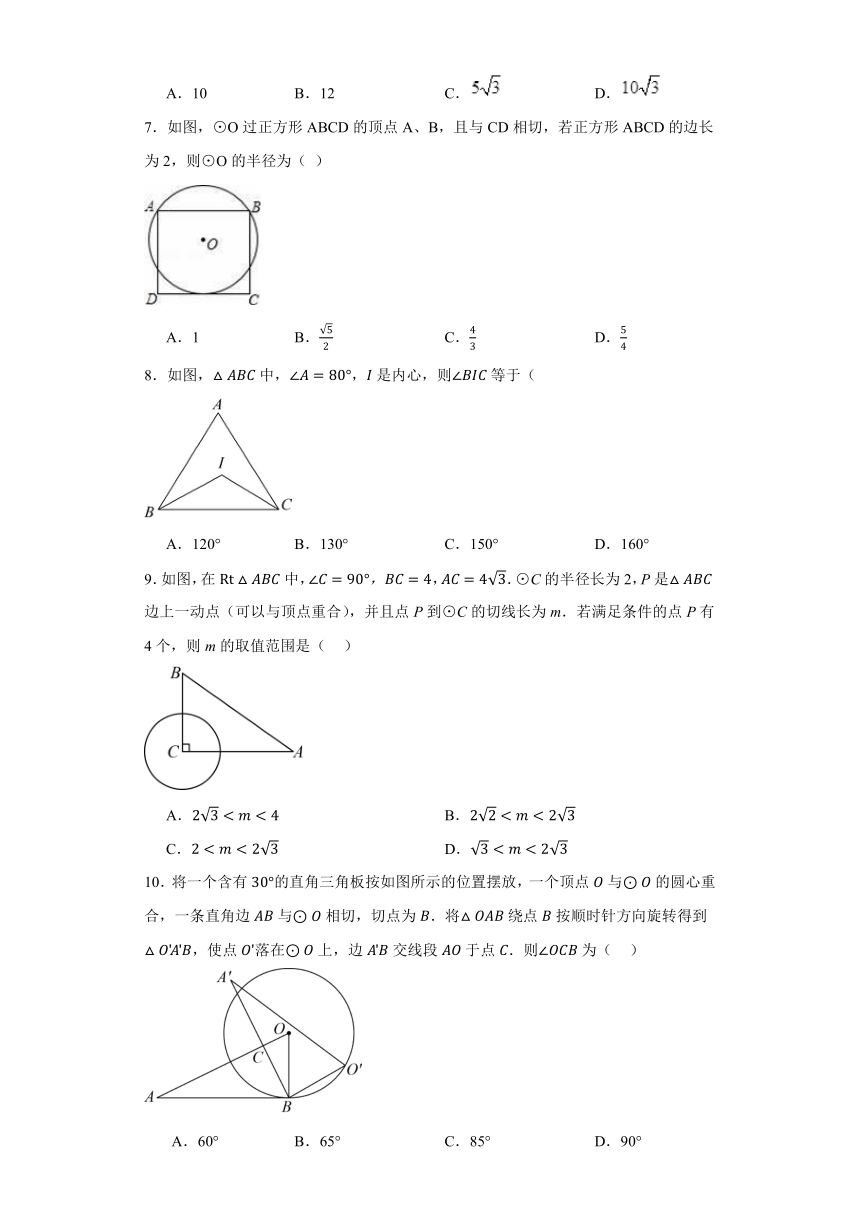
6.如图,从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60o,线段PA=10,那么弦AB的长是( )
A.10 B.12 C. D.
7.如图,⊙O过正方形ABCD的顶点A、B,且与CD相切,若正方形ABCD的边长为2,则⊙O的半径为( )
A.1 B. C. D.
8.如图,中,,是内心,则等于(
A.120° B.130° C.150° D.160°
9.如图,在中,,.⊙C的半径长为2,P是边上一动点(可以与顶点重合),并且点P到⊙C的切线长为m.若满足条件的点P有4个,则m的取值范围是( )
A. B.
C. D.
10.将一个含有的直角三角板按如图所示的位置摆放,一个顶点与的圆心重合,一条直角边与相切,切点为.将绕点按顺时针方向旋转得到,使点落在上,边交线段于点.则为( )
A.60° B.65° C.85° D.90°
二、填空题
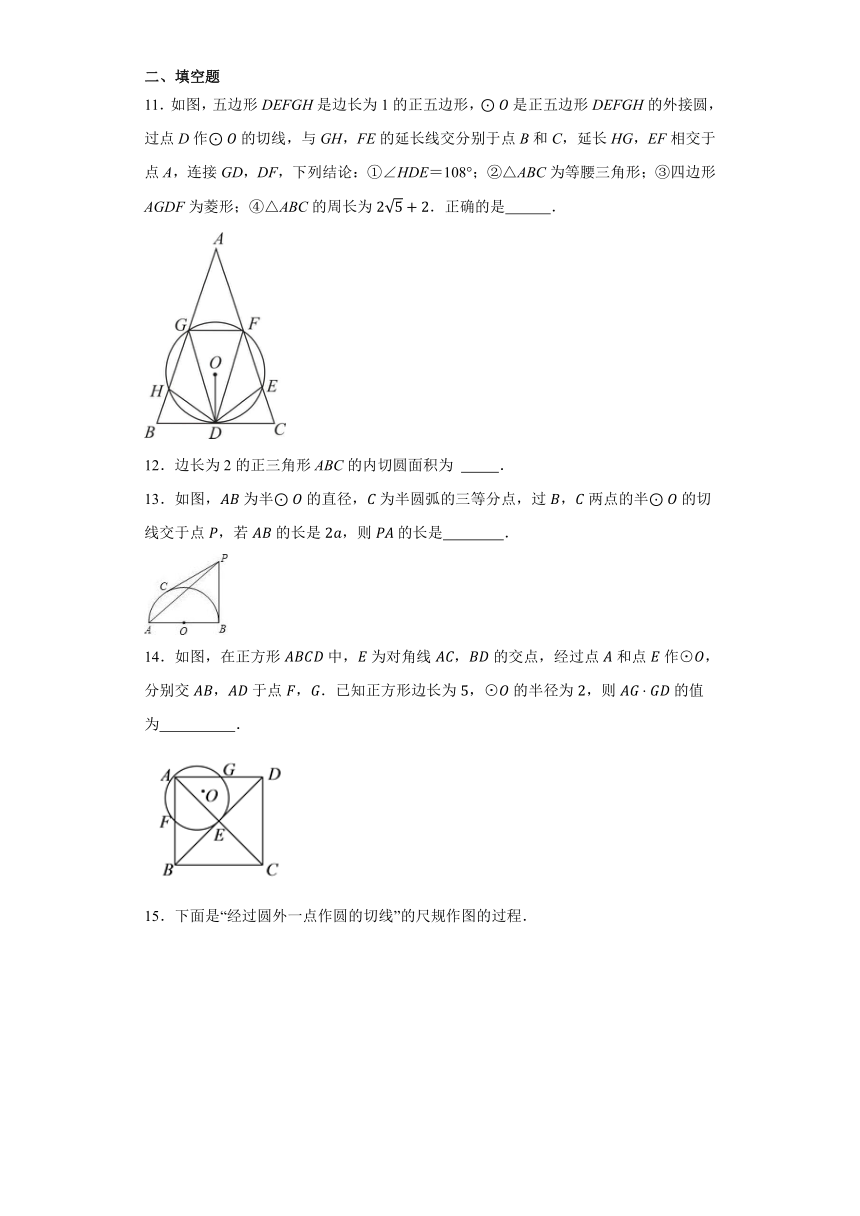
11.如图,五边形DEFGH是边长为1的正五边形,是正五边形DEFGH的外接圆,过点D作的切线,与GH,FE的延长线交分别于点B和C,延长HG,EF相交于点A,连接GD,DF,下列结论:①∠HDE=108°;②△ABC为等腰三角形;③四边形AGDF为菱形;④△ABC的周长为.正确的是 .
12.边长为2的正三角形ABC的内切圆面积为 .
13.如图,为半的直径,为半圆弧的三等分点,过,两点的半的切线交于点,若的长是,则的长是 .
14.如图,在正方形中,为对角线,的交点,经过点和点作⊙,分别交,于点,.已知正方形边长为,⊙的半径为,则的值为 .
15.下面是“经过圆外一点作圆的切线”的尺规作图的过程.
以上作图的依据是: .
三、解答题
16.如图,△ABC内接于⊙O,点D在⊙O上,且OD⊥BC,垂足为H,连接DC.
(1)求证:∠BCD=∠BAC;
(2)延长AB到点E,使EB=AC,连接DE.若DE与⊙O相切,试判断四边形BCDE的形状,并说明理由.
17.如图,内接于为直径,I是的内心,的延长线交于点D.
(1)求证:;
(2)连结,,若,求的长.
18.如图,为的直径,平分,于,交于.
(1)求证:为的切线;
(2)若,求的半径.
19.如图,为的直径,C,D为上的两点,,过点C作直线,交的延长线于点E,连接.
(1)试说明:是的切线.
(2)若,,求的长.
20.对于平面直角坐标系中的图形和点给出如下定义:如果图形上分别存在点,使得点Р为线段的中点,那么称点为图形的关联点.特别地,当三点重合时,点也为其关联点.已知点.
在点中,点的坐标为_ 时,点为线段,点的关联点;
的圆心为,半径为若点为,线段的关联点,求的取值范围;
的半径为,若点为,线段的关联点,求的取值范围;
点为上一点,以为圆心,为半径作圆,若点O为线段,的关联点,直接写出的取值范围.
21.图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图.
(1)蜘蛛在顶点A′处.
①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近;
(2)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.
一、单选题
1..已知⊙O1 的半径 r 为 4cm,⊙O2 的半径 R 为 5cm,两圆的圆心距 O1O2 为 6cm,则这两圆的位置关系是( )
A.相交 B.内含 C.内切 D.外切
2.如图所示,在中,,截的三边所得的弦长相等,则( )
A. B. C. D.
3.在直角坐标系中,我们把横、纵坐标都为整数的点叫做整点.对于一条直线,当它与一个圆的公共点都是整点时,我们把这条直线称为这个圆的“整点直线”.已知⊙O是以原点为圆心,半径为 圆,则⊙O的“整点直线”共有( )条
A.7 B.8 C.9 D.10
4.在下列说法中:①三角形的外心是三角形三边垂直平分线的交点;②若两条弧的度数相等,则它们是等弧;③直径是圆中最长的弦;④如果两条弦相等,那么这两条弦所对的圆心角相等;⑤圆的切线垂直于半径;其中说法正确的个数是( )
A.2 B.3 C.4 D.5
5.两圆的半径分别为R和r,圆心距为1,且R、r分别是方程的两个根,则两圆的位置关系是( )
A.相交 B.外切 C.内切 D.外离
6.如图,从⊙O外一点P引圆的两条切线PA、PB,切点分别是A、B,如果∠APB=60o,线段PA=10,那么弦AB的长是( )
A.10 B.12 C. D.
7.如图,⊙O过正方形ABCD的顶点A、B,且与CD相切,若正方形ABCD的边长为2,则⊙O的半径为( )
A.1 B. C. D.
8.如图,中,,是内心,则等于(
A.120° B.130° C.150° D.160°
9.如图,在中,,.⊙C的半径长为2,P是边上一动点(可以与顶点重合),并且点P到⊙C的切线长为m.若满足条件的点P有4个,则m的取值范围是( )
A. B.
C. D.
10.将一个含有的直角三角板按如图所示的位置摆放,一个顶点与的圆心重合,一条直角边与相切,切点为.将绕点按顺时针方向旋转得到,使点落在上,边交线段于点.则为( )
A.60° B.65° C.85° D.90°
二、填空题
11.如图,五边形DEFGH是边长为1的正五边形,是正五边形DEFGH的外接圆,过点D作的切线,与GH,FE的延长线交分别于点B和C,延长HG,EF相交于点A,连接GD,DF,下列结论:①∠HDE=108°;②△ABC为等腰三角形;③四边形AGDF为菱形;④△ABC的周长为.正确的是 .
12.边长为2的正三角形ABC的内切圆面积为 .
13.如图,为半的直径,为半圆弧的三等分点,过,两点的半的切线交于点,若的长是,则的长是 .
14.如图,在正方形中,为对角线,的交点,经过点和点作⊙,分别交,于点,.已知正方形边长为,⊙的半径为,则的值为 .
15.下面是“经过圆外一点作圆的切线”的尺规作图的过程.
以上作图的依据是: .
三、解答题
16.如图,△ABC内接于⊙O,点D在⊙O上,且OD⊥BC,垂足为H,连接DC.
(1)求证:∠BCD=∠BAC;
(2)延长AB到点E,使EB=AC,连接DE.若DE与⊙O相切,试判断四边形BCDE的形状,并说明理由.
17.如图,内接于为直径,I是的内心,的延长线交于点D.
(1)求证:;
(2)连结,,若,求的长.
18.如图,为的直径,平分,于,交于.
(1)求证:为的切线;
(2)若,求的半径.
19.如图,为的直径,C,D为上的两点,,过点C作直线,交的延长线于点E,连接.
(1)试说明:是的切线.
(2)若,,求的长.
20.对于平面直角坐标系中的图形和点给出如下定义:如果图形上分别存在点,使得点Р为线段的中点,那么称点为图形的关联点.特别地,当三点重合时,点也为其关联点.已知点.
在点中,点的坐标为_ 时,点为线段,点的关联点;
的圆心为,半径为若点为,线段的关联点,求的取值范围;
的半径为,若点为,线段的关联点,求的取值范围;
点为上一点,以为圆心,为半径作圆,若点O为线段,的关联点,直接写出的取值范围.
21.图1、图2为同一长方体房间的示意图,图3为该长方体的表面展开图.
(1)蜘蛛在顶点A′处.
①苍蝇在顶点B处时,试在图1中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;
②苍蝇在顶点C处时,图2中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近;
(2)在图3中,半径为10dm的⊙M与D′C′相切,圆心M到边CC′的距离为15dm,蜘蛛P在线段AB上,苍蝇Q在⊙M的圆周上,线段PQ为蜘蛛爬行路线,若PQ与⊙M相切,试求PQ长度的范围.
同课章节目录
